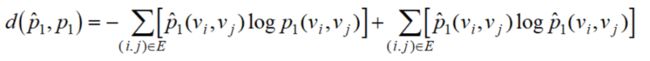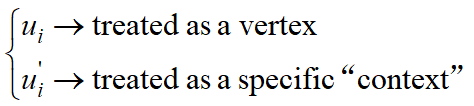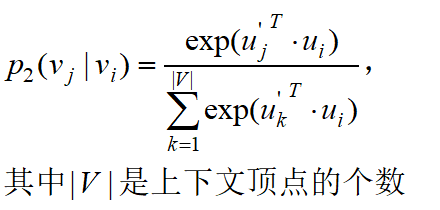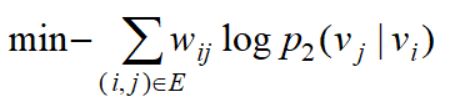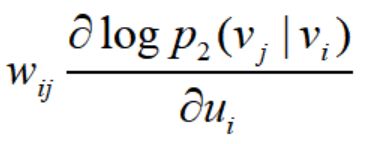Graph Embedding(二)
今天我们介绍Graph Embedding第二个算法——LINE(Large-scale Information Network Embedding)
![]()
一阶与二阶相似度
![]()
Deepwalk算法度量节点之间的相似性是根据是否有边相连决定的,LINE算法改变了这种度量方式,它引进了一阶相似度和二阶相似度。
一阶相似度(First-order Proximity)
对于无向图G(V,E)的每一条边edge(i,j),其相连的两个顶点vi和vj我们定义其一阶相似度:
同时定义其经验分布:
注意:wij不是上文中定义的一阶相似度pij
对于所有的V,引进KL散度衡量经验分布与一阶相似度的相似性:
注:KL散度=交叉熵-熵
我们希望这两个分布越接近越好,于是优化目标函数是:
这里说明一下为什么一阶相似度只适用于无向图,因为对于pij来说,具备对称性,即交换顶点vi和vj位置,结果不变;但对于有向图来说wij不一定等于wji
二阶相似度(Second-order Proximity)
二阶相似度适用于无向图和有向图两种情况,它的出发点是:每一个顶点扮演两个角色,一个是作为顶点的时候代表它自己,另一个是作为其他顶点的上下文(邻居),因此,把这两个角色用两个向量表示:
因此对于每一条边edge(i,j),定义在顶点vi下的 “context” vj 的条件概率:
|V|就是顶点的总数,上面公式是说对于顶点vi,各节点为其context的概率。进一步,如果p2(•|v1)和p2(•|v2)的概率分布是相似的(即v1和v2的context相似),那么这两个顶点就是相似的.
同样引进经验分布:
我们希望二阶相似度与经验分布越接近越好,同理使用KL散度衡量,最后要优化的目标函数是:
![]()
负采样优化目标
![]()
上一节,我们知道要优化的目标函数有两个:
为了使得图模型同时考虑一阶和二阶相似性,先分别训练两个相似度的向量表示,然后组合(直接拼接)在一起使用。
对于二阶相似度,直接优是比较困难的,采取负采样方法,每一条边edge(i,j)优化目标函数转为:
这里需要做个详细解释。
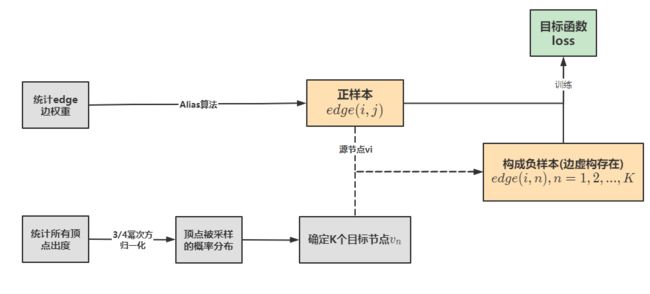
首先,对于一条有向边edge(i,j),顶点vi称为源节点,顶点vj称为目标节点,这是真实存在的一条边,我们称为正样本。负样本是指,vi作为源节点(固定),然后根据顶点出度对其他顶点进行采样,得到的顶点作为目标节点,这样子构成一条虚构的边,我们称为负样本:
对于负样本,要使得其概率尽可能低:
对于一阶相似度,也是采样同样的公式,只不过向量表示改一下即可:
![]()
参数求解
![]()
整个算法更新用到ASGD (Asynchronous Stochastic Gradient Algorithm) ,这里的学习率设置会有一点问题,因为其梯度是:
权重的大小将会影响梯度的数值,对于边权重方差较大的图,学习率设置太小太大都不合适,因此通过AliasMethod算法进行边采样来解决这个问题。
它实质把梯度公式的wij置为1或0,在获取正样本的时候,按照边的权重进行Alias采样,权重大的边被采样到的概率大,得到的边edge(i,j)作为正样本。之后利用负采样得到K个目标节点,与源节点vi构成负样本。因此,上一节的目标函数参数的更新公式是:
我们来看看原论文作者给出的核心代码,也是这么实现的:
// 使用 AliasMethod 进行边的采样, 得到源节点 u, 正样本 v
curedge = SampleAnEdge(gsl_rng_uniform(gsl_r), gsl_rng_uniform(gsl_r));
u = edge_source_id[curedge];
v = edge_target_id[curedge];
// dim 为 embedding 的大小, lu 表示 u 的 embedding 的起始位置, 因为矩阵使用数组来
// 表示, embedding 矩阵大小为 [N, emb], 表示成一维数组的大小为 N*emb, 要找到 u 所
// 代表的 emb, 需要用索引值 u 乘上 dim
lu = u * dim;
for (int c = 0; c != dim; c++) vec_error[c] = 0;
// NEGATIVE SAMPLING
for (int d = 0; d != num_negative + 1; d++)
{
if (d == 0)
{
target = v;
label = 1;
}
else
{
target = neg_table[Rand(seed)]; // 从 Negative Table 采样负样本
label = 0;
}
lv = target * dim;
// 如果使用一阶邻近, 那么 Update 的输入均为 emb_vertex
if (order == 1) Update(&emb_vertex[lu], &emb_vertex[lv], vec_error, label);
// 如果使用二阶邻近, 那么 Update 的输入分别为 emb_vertex 以及 emb_context
// emb_vertex 是节点作为自身所代表的 embedding,
// emb_context 是节点作为其他节点的 context 所代表的 embedding
if (order == 2) Update(&emb_vertex[lu], &emb_context[lv], vec_error, label);
}
// embedding 更新, 这个要根据对 loss 求导来得到, 具体见下面的讲解
for (int c = 0; c != dim; c++) emb_vertex[c + lu] += vec_error[c];
SGD更新函数如下:
/* Update embeddings */
void Update(real *vec_u, real *vec_v, real *vec_error, int label)
{
real x = 0, g;
for (int c = 0; c != dim; c++) x += vec_u[c] * vec_v[c];
g = (label - FastSigmoid(x)) * rho;
for (int c = 0; c != dim; c++) vec_error[c] += g * vec_v[c];
for (int c = 0; c != dim; c++) vec_v[c] += g * vec_u[c];
}
注:vec_u 为源节点的 embeddng, 而 vec_v 为目标节点的 embedding
![]()
算法实现
![]()
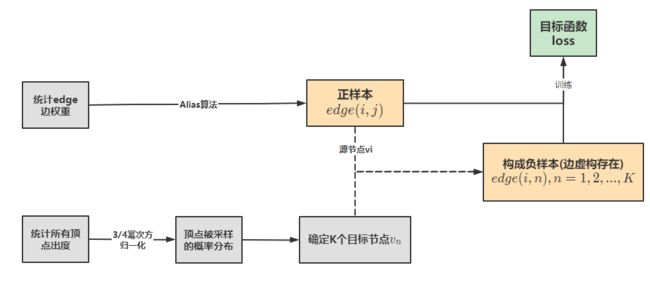
由此,我们得到LINE算法的流程图:
下面我们用python实现LINE算法。
先介绍整体思路首先,编写两个类,一个获取正负样本,一个获取节点的Embedding:
class Get_Line_Sample(object)
class Get_Line_Embedding(object)
其中,第一个类包含四个函数:
def sampling_and_save()
def positive_sample_pro()
def negative_sample_pro()
def Alias()
第二个函数获取边的采样概率,利用Alias算法生成两个数组——Prab数组和Alias数组,除此之外,还生成边的编码字典(保证边的唯一性)
传送门:离散采样——Alias Method
第三个函数是顶点的采样概率,这里直接输出每个顶点出度3/4幂次方的归一化概率。
然后,利用第一个函数去生成采样样本。其中负样本的生成逻辑是先生成一个列表,大小是迭代次数与每次迭代负样本个数的乘积:iter*K。元素是一系列顶点,每个顶点的频数约等于其出度概率。
然后,每次采样时,先生成一个正样本,再从上面那个列表中每次采样一个位置的元素,直到采样K个。不过这里和原论文不一样的地方是,若采样的负样本顶点是正样本源节点的近邻节点集合,则不采样(保证其负样本不是真是图中存在的边)。
第二个类一共有三个函数:
def train()
def update()
def sigmoid()
第三个函数就是计算sigmoid激活函数的值,第一个函数是进行模型训练,即更新embedding,这个函数实现迭代次数以及计算ASGD算法的误差,当误差达到一定阈值时停止迭代,返回结果。每个参数的梯度更新计算过程在第二个函数实现,之所以计算过程要另起一个函数,因为LINE分为一阶相似和二阶相似,这个函数只需要接收是一阶还是二阶的embedding即可。
下面是详细的代码。首先导入必要的模块:
import random
import numpy as np
import pandas as pd
import networkx as nx第一个类:
class Get_Line_Sample(object):
def __init__(self, edge_code, sample_list):
self.edge_code = edge_code
self.sample_list = sample_list
@classmethod
def sampling_and_save(cls, G, n_iter, K):
'''
:param G: 图模型,networkx形式
:param iter: 迭代次数,即采集正样本的个数
:param K: 每次迭代采样负样本的个数
'''
sample_list = [] # 接收采样样本
edge_code, Prab_table, Alias_table = cls.positive_sample_pro(G)
node_sample_pro = cls.negative_sample_pro(G)
Neg_table = []
for neg in node_sample_pro.keys():
num_node = int(node_sample_pro[neg] * K * n_iter)
li = [neg for i in range(num_node)]
Neg_table.extend(li)
for pos in range(n_iter):
a = random.randint(1, len(edge_code)) # 产生第一个随机数,1~N之间,N是边的个数
b = random.random() # 产生第二个随机,0~1之间
if b < Prab_table[a - 1]:
edge = a
else:
edge = Alias_table[a - 1]
source_node = edge_code[edge][0] # 正样本源节点
neigbor_nodes = list(G.neighbors(source_node)) # 源节点的所有邻居节点
neg_list = []
while len(neg_list) != K:
neg = random.choice(Neg_table) # 获取一个负样本
if neg in neigbor_nodes:
continue
else:
neg_list.append(neg)
neg_list.append(edge) # 把正样本存储到最后
sample_list.append(neg_list)
return cls(edge_code, sample_list)
@staticmethod
def positive_sample_pro(G):
'''
正样本采样概率表
:return: 每条边的编码以及对应的Alias表
'''
edge_weight = {(u, v): d['weight'] for (u, v, d) in G.edges(data=True)}
edge_z = sum(edge_weight.values()) # 边权重归一化因子
edge_weight = {key: value / edge_z for key, value in edge_weight.items()} # 权重归一化
edge_code = {n + 1: key for n, key in enumerate(edge_weight.keys())} # 对边进行编码化
Prob_li = list(edge_weight.values())
Prab_table, Alias_table = Get_Line_Sample.Alias(Prob_li) # 得到Alias算法结果表
return edge_code, Prab_table, Alias_table
@staticmethod
def negative_sample_pro(G):
'''
负样本采样概率表
:return:每个节点被采样到的概率
'''
s = G.number_of_nodes() - 1
node_out_degree = {n: int(d * s) ** (3 / 4) for n, d in nx.out_degree_centrality(G).items()} # 计算节点出度的3/4幂次方
z = sum(node_out_degree.values())
node_sample_pro = {n: i / z for n, i in node_out_degree.items()} # 每个顶点作为负采样的概率
return node_sample_pro
@staticmethod
def Alias(Prob_li):
'''
:param Prob_li: 事件对应的概率列表,索引代表事件
:return: 返回Prab和Alias列表
'''
M = len(Prob_li)
S = [M * i for i in Prob_li]
Prab_table = [1 for i in range(M)]
Alias_table = [0 for i in range(M)]
while True:
for i, s1 in enumerate(S):
if s1 < 1:
Prab_table[i] = s1
s0 = 1 - s1
for j, s2 in enumerate(S):
if s2 != 1 and s2 > s0 and i != j:
Alias_table[i] = j + 1
S[i] = 1
S[j] = s2 - s0
break
break
e = 1 - min(S)
if e < 0.000001:
break
return Prab_table, Alias_table第二个类:
class Get_Line_Embedding(object):
def __init__(self, G, edge_code, sample_list, dim):
'''
:param G: 图模型
:param edge_code: 接收来自Get_Line_Sample类的边的编码
:param sample_list: 接收来自Get_Line_Sample采样的样本
:param dim: embedding的维度
'''
self.dim = dim
self.edge_code = edge_code
self.sample_list = sample_list
self.emb_vertex = {node: np.random.uniform(0, 1, (dim, 1)) for node in G.nodes()} # 作为节点自身的表达
self.emb_context = {node: np.random.uniform(0, 1, (dim, 1)) for node in G.nodes()} # 作为其他节点上下文的表达
def train(self, iter_n=1000, order=2):
'''
:param iter_n: ASGD最大迭代次数
:param order: 一阶相似还是二阶,默认是二阶
:return: 更新后的embedding
'''
if order == 1:
emb_vertex, emb_context = self.emb_vertex, self.emb_vertex
else:
emb_vertex, emb_context = self.emb_vertex, self.emb_context
alpha = 0.001 # 学习率
e0 = 0
for epoch in range(iter_n):
per_vertex = {key: value.T.tolist()[0] for key, value in self.emb_vertex.items()}
per_context = {key: value.T.tolist()[0] for key, value in self.emb_context.items()}
self.update(emb_vertex, emb_context, alpha)
update_vertex = {key: value.T.tolist()[0] for key, value in self.emb_vertex.items()}
update_context = {key: value.T.tolist()[0] for key, value in self.emb_context.items()}
e_ver = sum([sum(i) for i in update_vertex.values()]) - sum([sum(i) for i in per_vertex.values()])
e_con = sum([sum(i) for i in update_context.values()]) - sum([sum(i) for i in per_context.values()])
e = abs(e_ver) + abs(e_con)
if e - e0 > 0 and epoch >= 1:
alpha = 0.1 * alpha
if abs(e) <= 0.000001:
print('ASGD early stop at epoch {},error {}'.format(epoch + 1, e))
break
else:
print('epoch {},error {}'.format(epoch + 1, e))
e0 = e
di_vertex = {key: value.T.tolist()[0] for key, value in self.emb_vertex.items()}
di_context = {key: value.T.tolist()[0] for key, value in self.emb_context.items()}
update_vertex = pd.DataFrame(di_vertex).T.sort_index()
update_context = pd.DataFrame(di_context).T.sort_index()
return update_vertex, update_context
def update(self, emb_vertex, emb_context, alpha):
'''
如果是一阶,传入的都是emb_vertex参数,即emb_context=emb_vertex,
:param emb_vertex: 节点作为自身的embedding
:param emb_context: 节点作为上下文的embedding
:param alpha: ASGD算法的学习率
:return:
'''
for sample in self.sample_list:
ui, uj = self.edge_code[sample[-1]] # 获取正样本源节点和目标节点
v = sample[:-1] # 获取K个负样本
g1 = 1 - self.sigmoid(np.dot(emb_context[uj].T, emb_vertex[ui]))
error_v = np.zeros((self.dim, 1))
for n in v:
g0 = 0 - self.sigmoid(np.dot(emb_context[n].T, emb_vertex[ui]))
error_v += g0 * emb_context[n]
emb_context[n] += alpha * g0 * emb_vertex[ui] # 更新负样本
emb_vertex[ui] += alpha * (g1 * emb_context[uj] + error_v) # 更新源节点
emb_context[uj] += alpha * g1 * emb_vertex[ui] # 更新目标节点
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))参考资料:
https://arxiv.org/pdf/1503.03578.pdf
https://github.com/tangjianpku/LINE
https://blog.csdn.net/Eric_1993/article/details/107573102