基于python手写深度学习网络系列(8)卷积神经网络的实现(结构、卷积层、池化层)
基于python手写深度学习网络系列(8)
卷积神经网络的实现(结构、卷积层、池化层)
CNN,很重要,主要用于图像识别、语音识别等场合。
7.1 整体结构
也是通过层的组装结合来搭建,但是相比之前的神经网络多了卷积层(convolution层)和池化层(Pooling层)
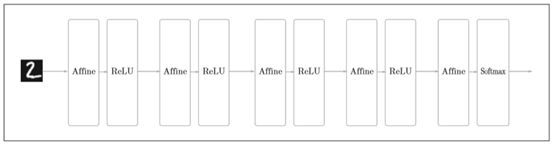
之前的神经网络,相邻层的神经元之间都会有连接,也就是全连接(fully-connected)
基于全连接层
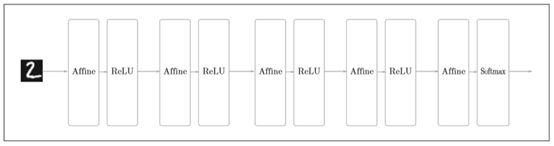
基于CNN网络
7.2 卷积层
全连接层有一个问题就是输出的形状被忽视了,三维数据一般都被拉成了一维的数据
但实际上,三维的数据,相邻的像素值比较接近,RGB各个通道之间有密切的关联性,较远的像素之间就没有关联了。
卷积层保持形状不变,有可能正确理解图像等具有形状的数据。CNN中有时将卷积层的输入输出数据称为特征图
卷积运算:相当于图像处理中的“滤波器运算”
(4,4)(3,3),最后输出大小(2,2)
对于输入数据,卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指图7-4中灰色的3×3的部分。如图7-4所示,将各个位置上滤 波器的元素和输入的对应元素相乘,然后再求和(有时将这个计算称为乘积累加运算)。然后,将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍,就可以得到卷积运算的输出。
CNN中,滤波器的参数就对应之前全连接层网络的权重。并且,CNN中也存在偏置。
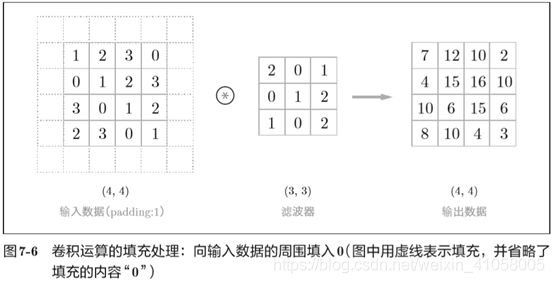
在进行卷积的处理前,有时需要对周围填入固定的数据,这叫做填充。(padding)
这个例子中将填充设成了1,不过填充的值也可以设置成2、3等任意的整数。在图7-5 的例子中,如果将填充设为2,则输入数据的大小变为(8,8);如果将填充设为3,则大小变为(10, 10)。
只要填充1就可以保证图像的大小不发生变化
应用滤波器的位置间隔称为步幅(stride)。之前的例子中步幅都是1,如果将步幅设为2,则如图7-7所示,应用滤波器的窗口的间隔变为2个元素
在考虑卷积运算有时是三维的
可以发现纵深方向(通道方向)上特征图增加了。通道方向上有多个特征图时,会按通道进行输入数据和滤波器的卷积运算,并将结果相加,从而得到输出。
输入数据和滤波器的通道数要设为相同的值。在这个例子中,输入数据和滤波器的通道数一致,均为3。
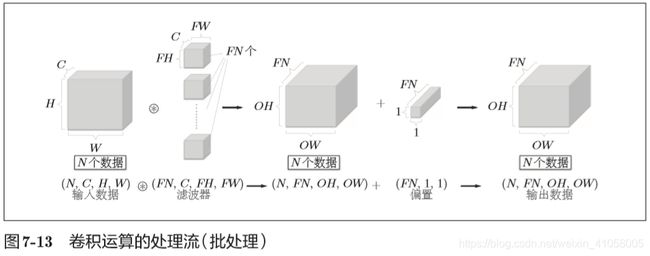
书写顺序为(channel, height, width)。比如,通道数为C、高度为H、长度为W的数据的形状可以写成(C, H,W)。滤波器也一样,要按(channel,height, width)的顺序书写。比如,通道数为C、滤波器高度为FH(Filter Height)、长度为FW(Filter Width)时,可以写成(C,FH,FW)。
这种卷积最后得到的是1张特征图,那要是在通道方向上也拥有多个卷积运算的输出,就需要多个滤波器
作为4维数据,滤波器的权重数据要按(output_channel,input_channel, height, width)的顺序书写。
每个通道只有一个偏置。这里,偏置的形状是(FN,1,1), 滤波器的输出结果的形状是(FN, OH, OW)。这两个方块相加时,要对滤波器的输出结果(FN,OH,OW)按通道加上相同的偏置值。
若是还需要批处理,就要把数据保存为四维数据
7.3 池化层
池化是缩小高、长方向上的空间的运算
除了max池化,还有average池化,一般来说,池化的窗口大小会和步幅设定成一样的值
池化层没有要学习的参数,输入数据和输出数据的通道数不会发生变化,计算是按通道独立进行。对输入数据发生微小变卦具有鲁棒性(健壮)
7.4 卷积层和池化层的实现
生成四维数组,访问每一个数据,用x[0]或者x[1]即可;访问第一个数据第一个通道的二维数据可以用x[0,0]或者是x[0][0]
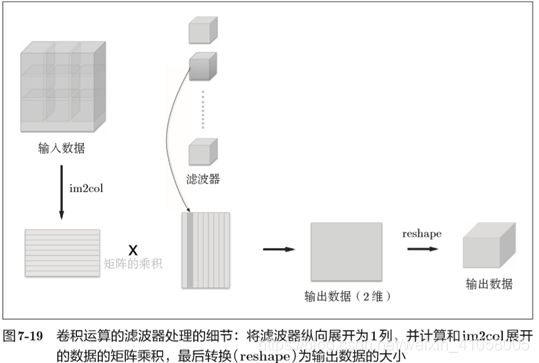
针对多层的卷积,全部使用for循环会变慢,numpy有这个特点,所以这里使用im2col(image to column)这个函数来实现:
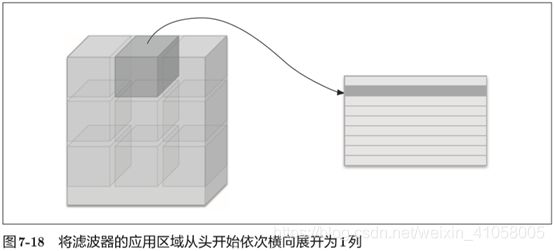
对3维或者4维数据应用,应用im2col后,变成二维矩阵,以适应滤波器。将应用滤波器的区域(3维方块)横向展开为1列。im2col会在所有应用滤波器的地方进行这个展开处理。
步幅比较小的时候,展开后的个数会多于原方块的元素个数,会消耗更多的内存
卷积层的实现
reshape将各个滤波器的方块纵向展开为1列。这里通过reshape(FN,-1)将参数指定为-1,这是reshape的一个便利的功能。通过在reshape时指定为-1,reshape函数会自动计算-1维度上的元素个数,以使多维数组的元素个数前后一致
(10, 3, 5, 5)形状的数组的元素个数共有750个,指定reshape(10,-1)后,就 会转换成(10, 75)形状的数组。
Forward中最后将输出的大小转换成合适的形状,使用了numpy中的transpose函数。transpose会更改多维数组的轴的顺序。如图7-20 所示,通过指定从0开始的索引(编号)序列,就可以更改轴的顺序。
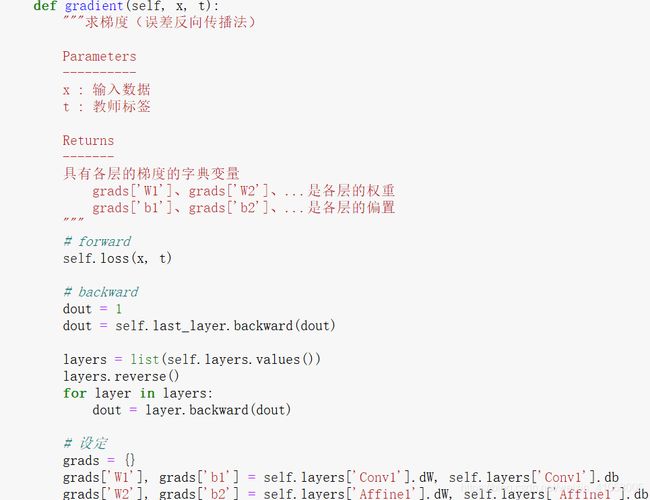
进行卷积层的反向传播时,要进行逆处理,比如说使用col2im函数
卷积层的实现;
池化的实现
7.5 CNN实现
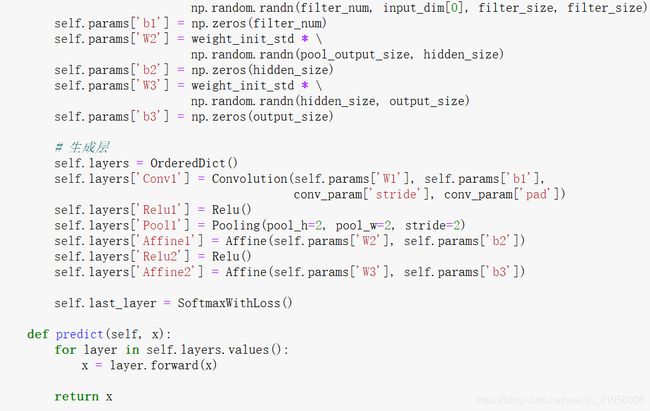
基于上面这些层,搭建CNN网络
学习所需的参数是第1层的卷积层和剩余两个全连接层的权重和偏置。 将这些参数保存在实例变量的params字典中。将第1层的卷积层的权重设为 关键字W1,偏置设为关键字b1。同样,分别用关键字W2、b2和关键字W3、b3 来保存第2个和第3个全连接层的权重和偏置。
向有向字典的layers中添加层
7.6CNN可视化
学习前的滤波器是随机进行初始化的,所以在黑白的浓淡上没有规律可循,但学习后的滤波器变成了有规律的图像,比如从白到黑渐变的滤波器、含有块状区域(称为blob)的滤波器等。
滤波器在观察什么?在观察边缘(颜色变化的分界线)和斑块(局部的块状区域)等。比如,左半部分为白色、右半部分为黑色的滤波器的情况下,如图7-25所示,会对垂直方向上的边缘有响应。
由此可知,卷积层的滤波器会提取边缘或斑块等原始信息。而刚才实现的CNN会将这些原始信息传递给后面的层。
AlexNet堆叠了多层卷积层和池化层
如果堆叠了多层卷积层,则随着层次加深,提取的信息也愈加复杂、抽象,这是深度学习中很有意思的一个地方。最开始的层对简单的边缘有响应,接下来的层对纹理有响应,再后面的层对更加复杂的物体部件有响应。也就是说,随着层次加深,神经元从简单的形状向“高级”信息变化。换句话说,就像我们理解东西的“含义”一样,响应的对象在逐渐变化。
7.7代表性的CNN网络
1998年提出的LeNet【20】
2012年提出的AlexNet【21】
[20] Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner(1998): Gradient-based
learning applied to document recognition. Proceedings of the IEEE 86,
11 (November 1998), 2278 – 2324.
[21] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton(2012) :
ImageNet Classification with Deep Convolutional Neural Networks.
In F. Pereira, C. J. C. Burges, L. Bottou, & K. Q. Weinberger, eds.
Advances in Neural Information Processing Systems 25. Curran
Associates, Inc., 1097 – 1105.
LeNet1998年被提出,它有连续的卷积层和池化层(正确地讲,是只“抽选元素”的子采样层),最后经全连接层输出结果。
与现在的不同点:LeNet中使用sigmoid函数,而现在的CNN中主要使用ReLU函数。 此外,原始的LeNet中使用子采样(subsampling)缩小中间数据的大小,而 现在的CNN中Max池化是主流。