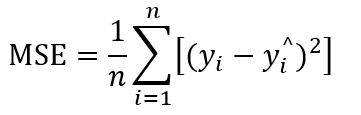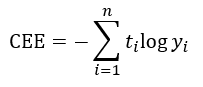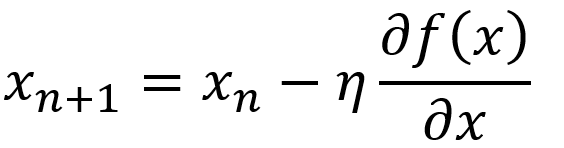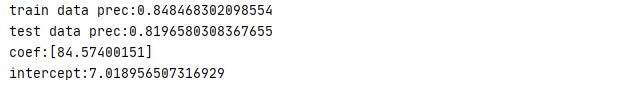Python 机器学习实战 —— 监督学习（上）

前言

近年来AI人工智能成为社会发展趋势，在IT行业引起一波热潮，有关机器学习、深度学习、神经网络等文章多不胜数。从智能家居、自动驾驶、无人机、智能机器人到人造卫星、安防军备，无论是国家级军事设备还是广泛的民用设施，都充斥着AI应用的身影。接下来的一系列文章将会由浅入深从不同角度分别介绍机器学习、深度学习之间的关系与区别，通过一系统的常用案例讲述它们的应用场景。
本文将会从最常见的机器学习开始介绍相关的知识应用与开发流程。

目录

一、浅谈机器学习

 二、基本概念

三、常用方法介绍

四、线性模型

五、支持向量机

六、k近邻

七、朴素贝叶斯分类 

八、决策树

---

一、浅谈机器学习

1.1 机器学习简介

其实AI人工智能并非近代的产物，早在19世纪的50到80年代，科学家们就有着让计算机算法代替人脑思考的想法。通过几十年的努力，到了90年代成为了机器学习蓬勃发展期，很多科技公司在不同领域提供了相关的技术支持。在最初，机器学习只用于垃圾邮件清理，数学公式分析等简单领域，然而后来其应用场景越来越多，无论是图片过滤，语音分析，数据清洗等领域都能看到机器学习的身影。到如今无论是智能手机，航空运输，智能驾驶等方方面面都可以看到 AI 的身影。

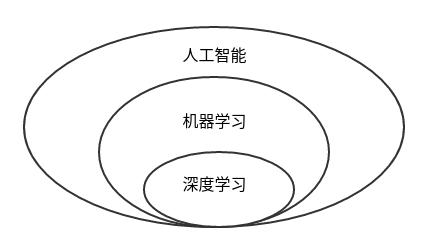
从不同领域分析，AI人工智能包含了机器学习与深度学习。

机器学习主要应用数据科学领域，它与普通程序开发的主要区别在于一般程序，数据往往来源于不同的数据库，通过对数据进行复杂转化，运算得到最后的结果。
而机器学习目的并不是为了得到最后的运算结果，而是对计算过程进行分析，总结出一套运算的规则。只要数据量足够多，运算规则就越准确。最后可以根据这套规则对没有通过验证的数据进行预算，得到预算后的值。只要使用的规则正确，预算的结果的正确率往往可以达到95%以上。 

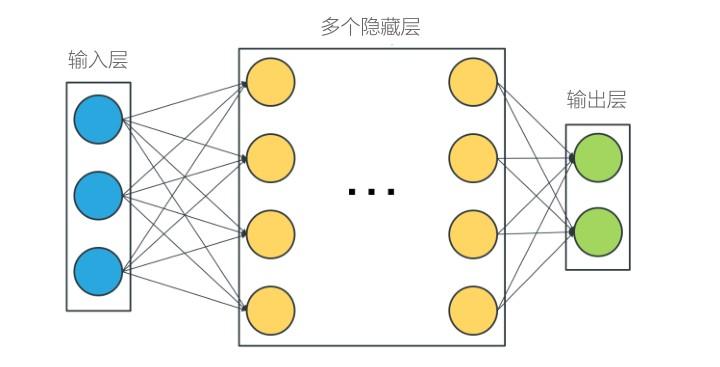
而深度学习开始只是机器学习的一分支领域，它更强调从连续的层中进行学习，这种层级结构中的每一层代表不同程序的抽象，层级越高，抽象程度越大。这些层主要通过神经网络的模型学习得到的，最大的模型会有上百层之多。而最简单的神经网络分为输入层，中间层（中间层往往会包含多个隐藏层），输出层。

经过多年的发展，深度学习的应用层面越来越广，从而诞生出 Tensorflow、Keras、Theano、CNTK 等框架的支持，逐渐发展形成独立的技术领域。根据不同的应用场景，深度学习又分为多层感知器MLP、深度神经网络DNN、卷积神经网络CNN、递归神经网络RNN、生成对抗网络BNN等多个方面。

由于本系统文章主要是对机器学习进行介绍，对深度学习有兴趣有朋友可以留意后面的文章，将会对神经网络进行更深入全面的讲解。

1.2  机器学习分类

机器学习可分为监督学习与无监督学习两种

1.2.1  监督学习

从输入 / 输出中总结运算规律进行机械学习的算法叫做监督学习。在监督学习中，每个实例都是由一个输入对象（通常为矢量）和一个期望的输出值（也称为监督信号）组成。监督学习算法是分析该数据的输入对象与输出值 ，总结当中的运算规律并产生一个推断的逻辑，并可以把此逻辑用于映射出的新实例，对没有运算过的数据结果进行预测。
其过程就像读小学时候的数学应用题，课堂上老师会先讲解应用题的公式与计算方法，然后学生可以在做作业时根据此计算规律完成类似的题目。

常见的监督学习包含了线性回归、k近邻、朴素贝叶斯分类 、决策树、随机森林与梯度提升决策树、支持向量机等多种算法，在下面将用不同实例介绍其应用场景。

1.2..2  无监督学习

相比之下无监督学习只有输入数据，没有提供输出结果，只能通过计算评估其中的运行规律。就好比在考试中遇到作业上没有做过的应用题，只能通过思考总结才能得出答案。它的最大挑战在于实例没有包含最终结果，所以无法在学习中评估算法是否学到了有用的东西。

常见的无监督学习分为聚类、降维两大类，包含了PCA（主成分分析）、NMF（非负矩阵分解）、t-SNE（流形学习）、k均值聚类、DBSCAN 等多种算法，将在下一篇文章 《 Python 机器学习实战 —— 无监督学习》中详细介绍，敬请留意。

 二、基本概念

在机器学习里，每一行的数据实例被看作是一个样本，每一列的数据被看作是一个特征。学过面向对象开发的朋友应该好理解，这相当于一个类与其属性的关系。而监督学习是通过一系列样本计算，总结出特征与计算结果之间的关系，这被称为特征提取。

2.1 分类与回归的区别

监督学习分成分类与回归两大类：分类与回归
分类的目标是预测类别标签，类似于通过人脸识别分出黄种人、白种人、黑种人。
回归的目标则是预测一个连续值，相当于数学里面的坐标图，它可以通过已有的数据计算出坐标的走向，从而对末知值进行预测。类似于气温预计，GDP增速预算。
其实区分分类与回归很简单，只要判断输出值是否具备连续性，具有连续性的就是回归，只有若干个固定值的就是分类。

2.2 数据划分

从监督学习的概念可以了解，其学习目标是要从已有的数据中总结出各个特征与结果之间的关系，然而这个计算模型的泛化能力如何，我们无法从已通过运算过的数据中得知。所以在运算前，一般会先对数据进行划分，一部分是训练数据，专门用作模型的学习，另一部分是测试数据，用作模型的测试，其比例一般是75%对25%。
为了方便数据划分，sklearn 提供 train_test_split 函数方便日常使用，下一节将有介绍。

2.3  过拟合与欠拟合

对于训练数据最重要的目标是将其泛化，总结出每个特征的比重，因此并非正确率越高越好。如果在训练过程中，得到的正确率是100%，然而在测试时候，正常率却很低，不能泛化到测试数据当中。这往往是因为训练过程中存在过似合，过度重视某些特征，而忽略某些关键因素。
相反，如果模型过分简单，考虑的因素太少，甚至导致在训练过程中的正确率就很低，这可能就是因为模型的欠拟合造成。

所以在选择模型的时候，需要在过拟合与欠拟合之间作出权衡（如图）。

2.4 损失函数

损失函数一方面跟数学计算原理的应用关系比较密切，另一个方面它也是机器学习的基层原理，此章节想做一个简单的介绍。由于网上关于这方面的学习材料很多，所以此章节主要是想通过最容易理解的方式去讲述计算的原理，至于复杂的计算流程可以在网上查找。
在写这篇文章的时候，恰好是高考的开考日，在这里预祝师弟师妹能顺利闯关，金榜题名。毕竟最近疫情有复发的情况，学习实在不容易。通过此章节想告诉理工科的学子们，辛勤学习并非一无所用。公式里所蕴藏的原理，他日参加工作时候还是有很广的应用场景。

在日常对数据模型的测试中，预测值与真实值总会存在一定的偏差，以直线方程 y=a*x+b 为例，如下图。在预测值 [x1,y1]  [x2,y2]  [x3,y3]  ....... [x(i),y(i)] 中,并非每个点与方程匹配，而是存在一定的误差。所以在测试中，当误差值最小时，可以看作这条直线的正确答案。

损失函数就是用来评价模型的预测值和真实值不一样的程度，当损失值越小，证明预计值越接近真实值，模型的训练程度就越好。为了让预测值 y^ (i)  尽量接近于真实值 y(i) ，学者提出了多个方法进行计算损失值，最常见的损失函数有均方误差（MSE）、交叉熵误差（CEE）等。
均方误差（MSE）中，因为每个预测值与真实值大小不同，为了解决差值的正负值之分，所以误差大小就用差值平方来表示，差值越小，平方值小，误差越小。
均方误差计算公式就是求预测值与真实值之间的方差平均值，如果均方误差越小，那就证明预测值越接近于真实值。

交叉熵误差（CEE）的公式如下，其中  为实际的分类结果，  为预测的结果

把它用于分类模型时有一个很好的特性，可以真实的反应出真实分类结果和预测结果的误差，假设 , 即真实的分类结果是 , 则 交叉熵误差可以简化为  ，那函数图像如下。可以看到， 越接近 ，即预测结果和真实分类结果越接近，误差越接近， 即误差越小。

 

关于损失函数有多种算法，下面介绍两种最常用也是最容易理解的算法：最小二乘法（OLS）与梯度下降法（GD）

 2.4.1 最小二乘法

最小二乘法是基于 MSE 均方误差而来，它的目标就是求出 n 个 y^ (i) 与 y(i) 误差值平方和最小时各常量参数的值。还是以上面提到的直线方程 y=a*x+b 为例，均方误差越小，证明预测值越接近于真实值，这时候只要求出最小均方误差时 a，b的值，也就可以得出此直线的方程。因为 n 是个常数，所以求最小均方误差的公式可以转化为求预测值 y^ (i) 与真实值之 y(i) 间的最小方差，这就是最小二乘法的由来。

 代入  y=a*x+b  后，计算公式可得到转换成下图，由于计算的是平方和，所以表达式必然存在最小值，通过偏导数为 0 时得极值的原理，可得到计算公式：

此时好办，最小二乘法已经变成高考的导数题，要了解求解过程的程序猿建议去复习一下高考时偏导数求解的方法（若怕麻烦通过几条简单的语法计算也可得到最终结果）。根据以下得出的公式，代入已知的数据点  [x1,y1]  [x2,y2]  [x3,y3]  ....... [x(i),y(i)]  便可得到最后的 a、b 参数值，最后把 a、b 值代入直线方程就是最终的答案。

第四节介绍的线性回归模型中，有部分就是使用最小二乘法来实现的，敬请留意。
当然，现实情形下数据模型是复杂的，不可能完全按照直线模型来走，所以复杂的线性模型还可以通过多次方程式，基函数，线性分割等多种方法来处理，在后面章节将会详细讲述。

2.4.2 梯度下降法

上面提到损失函数就是用来评价模型的预测值和真实值不一样的程度，损失值越小证明参数的预测值越接近于真实值。梯度下降法就是用于求损失值最小时的参数值，相对于最小二乘法复杂的数学公式，它可以通过偏导数斜率的变化更形象地描述解决的过程。

先介绍梯度下降法用到的基本概念：
切线斜率：从数学的角度可知，一维函数在点 x 的导数叫做函数在点 x 的切线斜率，二维函数在点（x0,x1) 的偏导数称为点（x0,x1) 的切线斜率，如此类推。
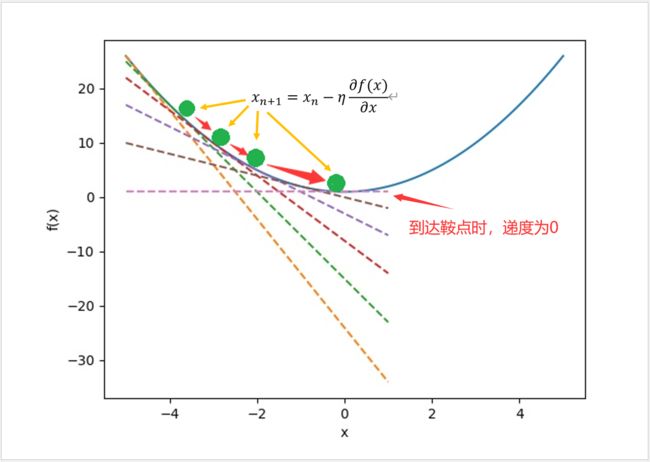
鞍点：函数的极小值（最小值）被称为鞍点，从数学原理可知当到达鞍点时，切线斜率接近于 0。
梯度：以常用的二元方程 f(x0,x1)=x02+x12  为例子，把全部变量的偏导数（切线斜率）汇总成的向量称为梯度

下面以一个二次方程 f(x)=x2+1 为例，介绍一下如何通过梯度下降法求极值
首先，切线的斜率可以通过导数原理求得，例如 f(x) 分别经过点 A(- 4,17) ，B(- 5,26)，此时会发现，两点之间的距离越小，它们所组成的直线就越接近于该点的切线。两点距离无限接近于0时，此时可认为这条直线就是该点的切线，这也是微积分的基本原理。

下面的例子就是实现上述的原理，画出与点（- 4,17)  间 x 轴的距离分别为 0.3、0.2、0.001，0.0001 的直线。调用 tangent（）可以返回该直线的斜率，当 h 使用默认值 0.0001 值，该直线斜率已经无限接近于导数值（即切线斜率）。

 1 class gradinet_drop():
 2     def __init__(self):
 3         return
 4 
 5     def f(self, x):
 6         return x*x+1
 7 
 8     def polt_line(self):
 9         # 画出 y=x*x+1 图
10         x = np.linspace(-5, 5, 100)
11         plt.plot(x.reshape(-1, 1), self.f(x))
12         plt.xlabel('x')
13         plt.ylabel('f(x)')
14 
15     def tangent(seft,x,h=0.0001):
16         #根据 y=ax+b 直线公式
17         #求导数，即切线斜率
18         a=(seft.f(x+h)-seft.f(x))/h
19         #求截距
20         b=seft.f(x+h)-a*x+h
21         #划出切线
22         seft.polt_tangent(a,b)
23         return a
24 
25     def polt_tangent(self,a,b):
26         #划出直线 y=ax+b
27         x = np.linspace(-5, -1, 100)
28         y=a*x+b
29         plt.plot(x.reshape(-1,1),y,'--')
30 
31 gradientdrop=gradinet_drop()
32 gradientdrop.polt_line()
33 # 分别以 h 等于 -0.3，-0.2，-0.001 ,0.0001求斜率
34 # 将发现 h 越小，所得斜率越接于近切线斜率
35 for h in [-0.3,-0.2,0.001,0.0001]:
36     print('h={0}, tangent={1}'.format(h,gradientdrop.tangent(-4,h)))
37 plt.show()

运行结果

梯度下降法最终的目标是求得切线斜率接近无限于0时的数据点（鞍点）， 所以函数可以使用最简单的方法，使取值沿着当前梯度方向不断前进，然后重复计算梯度。通过此递归方式，切线斜率就是无限接近于0。
用数学公式表达如下图，η 表示学习率，学习率可以根据实际需要而改变，将学习率乘以该点的切线斜率代表学习量。

根据此公式，可以在上面的代码中加入一个简单的方法gradient()，以 0.01 的学习率，重复1000次进行计算。随着梯度不断地下降，x 坐标就会根据学习量不断接近鞍点，在重复1000后可以看到在数据点（0，1）处的切线斜率 tangent 为 -1.0098588631990424e-08，已无限接近于 0 ，此时鞍点的函数值 f(x)=1 就是此函数的最小值。

 1 class gradinet_drop():
 2     def __init__(self):
 3         return
 4 
 5     def f(self, x):
 6         return x*x+1
 7 
 8     def polt_line(self):
 9         # 画出 y=x*x+1 图
10         x = np.linspace(-5, 5, 100)
11         plt.plot(x.reshape(-1, 1), self.f(x))
12         plt.xlabel('x')
13         plt.ylabel('f(x)')
14 
15     def tangent(seft,x,h=0.0001):
16         #根据 y=ax+b 直线公式
17         #求导数（切线斜率）
18         a=(seft.f(x+h)-seft.f(x))/h
19         #求截距
20         b=seft.f(x+h)-a*x+h
21         #随机画出切线
22         n=np.random.randint(100)
23         if(n==5):
24             seft.polt_tangent(a,b)
25         return a
26 
27     def polt_tangent(self,a,b):
28         #划出切线 y=ax+b
29         x = np.linspace(-5, 1, 100)
30         y=a*x+b
31         plt.plot(x.reshape(-1,1),y,'--')
32 
33     def gradinet(seft,x,rate=0.01,n=1000):
34         #学习率默认为0.01，默认重复1000次
35         for i in range(n):
36             x-=seft.tangent(x)*rate
37             print('x={0},f(x)={1},tangent slope={2}'.format(x,seft.f(x),seft.tangent(x)))
38 
39 gradientdrop=gradinet_drop()
40 gradientdrop.polt_line()
41 #使用学习率默认0.01，默认重复1000次求出鞍点
42 gradientdrop.gradinet(-3)
43 plt.show()

运行结果

 

到此不防思考一下使用梯度下降法找到鞍点的目标是什么，其实只要把简单的二次方程 f(x) 替换成为损失函数便会豁然开朗。以均方误差 MSE 为例，当找到鞍点，意味着找到函数最小值，即在该点时均方误差最小，在这点得到的参数值就是该函数的常量。
同样以最小二乘法中的直线 y=a*x+b 为例，把代码稍微修改一下。首先把方程改为均方误差公式，通过 sympy 包中的函数 diff 分别对 a，b 求偏导数，把学习率设置为0.01，训练1000次，a，b的默认初始值均为 1。使用 sklearn 中的测试数据 make_regression 进行训练，最后画出该直线并输出斜率和截距。

 1 class gradinet_drop():
 2     def __init__(self,train_x,train_y):
 3         #定义测试数据
 4         self.x=train_x
 5         self.y=train_y
 6         return
 7 
 8     def mes(self,a,b):
 9         #均方误差计算公式
10         return mean((self.y-a*self.x-b)**2)
11 
12     def partial_derivative(seft):
13         #求 mes(a,b)对 a,b 的偏导数
14         partial_derivative_a=sp.diff(seft.mes(a,b), a)
15         partial_derivative_b=sp.diff(seft.mes(a,b),b)
16         return [partial_derivative_a,partial_derivative_b]
17 
18     def gradinet(seft,rate=0.01,n=1000):
19         #学习率默认为0.01，默认重复1000次
20         #把 y=a*x+b 参数 a,b 的初始值设为 1，1
21         a1=1
22         b1=1
23         #默认训练1000次，找到最小均方误差时的 a,b 值
24         for i in range(n):
25             deri=seft.partial_derivative()
26             a1-=deri[0].subs({a:a1,b:b1})*rate
27             b1-=deri[1].subs({a:a1,b:b1})*rate
28         #输出直线参数 a,b 值
29         print('y=a*x=b\n  a={0},b={1}'.format(a1,b1))
30         return [a1,b1]
31 
32     def polt_line(self,param):
33         #根据a,b参数值划出直线 y=a*x+b
34         x = np.linspace(-3, 3, 100)
35         y=param[0]*x+param[1]
36         plt.plot(x,y,20)
37         plt.legend(['train data','line'])
38 
39 #输入测试数据
40 X,y=dataset.make_regression(n_features=1,noise=5)
41 gradient_drop=gradinet_drop(np.squeeze(X),y)
42 #画出数据点
43 plt.plot(X,y,'.')
44 #训练数据找出最小均方误差时的参数 a,b 值
45 param=gradient_drop.gradinet()
46 #画出训练后的直线
47 gradient_drop.polt_line(param)
48 plt.show()

运行结果

 

可见计算后的直线与训练库中的点已相当接近，使用梯度下降法只需要牢记一点：计算目标是求出鞍点，在损失值最低时的参数值就是该函数的常量。下面介绍到的 SGD 模型正是使用梯度下降法进行计算，后面将有详细说明。
对损失函数就介绍到这里，希望对各位的理解有所帮助。

三、常用方法介绍

Scikit-Learn 是目录最常用的机器学习库，所以在本文当中大部实例都是运用当中的方法完成。
在 sklearn.datasets 中包含了大量的数据集，可为运算提供测试案例。例如鸢尾花数据集 load_iris()、癌症数据集 load_breast_cancer()、波士顿放假数据集 load_boston() 这些都是各大技术文章里常用的数据集，为了方便阅读下面大部分的例子中都会用到这些数据作为例子进行解说。

3.1  train_test_split 方法

上面曾经提起，为了方便区分训练数据与测试数据，sklearn 提供了 train_test_split 方法去划分训练数据与测试数据

 train_test_split( * arrays,  test_size=None,   train_size=None, random_state=None, shuffle=True,stratify=None)

• *arrays：可以是列表、numpy数组、scipy稀疏矩阵或pandas的数据框

• test_size：可以为浮点、整数或None，默认为None

　　　　①若为浮点时，表示测试集占总样本的百分比

　　　　②若为整数时，表示测试样本样本数

　　　　③若为None时，test size自动设置成0.25

• train_size：可以为浮点、整数或None，默认为None

　　　　①若为浮点时，表示训练集占总样本的百分比

　　　　②若为整数时，表示训练样本的样本数

　　　　③若为None时，train_size自动被设置成0.75

• random_state：可以为整数、RandomState实例或None，默认为None

　　　　①若为None时，每次生成的数据都是随机，可能不一样

　　　　②若为整数时，每次生成的数据都相同

• stratify：可以为类似数组或None

　　　　①若为None时，划分出来的测试集或训练集中，其类标签的比例也是随机的

　　　　②若不为None时，划分出来的测试集或训练集中，其类标签的比例同输入的数组中类标签的比例相同，用于处理不均衡数据集

常用例子：

把1000个数据集按 75% 与 25% 的比例划分为训练数据与测试数据

1     X,y=make_wave(1000)
2     X_train,X_test,y_train,y_test=train_test_split(X,y)

 train_size 与 test_size 默认值为75% 与 25% ，所以上面的例子与下面例子得出结果相同

1     X,y=make_wave(1000)
2     X_train,X_test,y_train,y_test=train_test_split(X,y,train_size=0.75,test_size=0.25)

为了每次测试得到相同的数据集，可以把 RandomState 设置为相同值，只要RandomState相同，则产生的数据集相同。
因为 RandomState 默认为空，因此在不填写的情况下，每次产生的数据集都是随机数据

1     X,y=make_wave(1000)
2     X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)

3.2 predict 方法与 accuracy_score 方法

在分类模型中，通常使用 predict（selt, X：any）方法预测新数据的标签，通常在完成训练后，就是通过此方法输入测试数据，把计算结果与测试结果进行对比。
accuracy_score 主要用于对比预测结果的准备率
下面的代码就是最简单的流程，先划分训练数据与测试数据，然后选择模型，输入训练数据进行泛化，输入测试数据求出计算结果，最后把计算结果与已有的测试结果进行对比，查看其正确率。

 1     X,y=make_blobs(n_samples=150,n_features=2)
 2     #划分训练数据与测试数据
 3     X_train,X_test,y_train,y_test=train_test_split(X,y)
 4     #绑定模型
 5     knn_classifier=KNeighborsClassifier(n_neighbors=7)
 6     #输入训练数据
 7     knn_classifier.fit(X_train,y_train)
 8     #运行测试数据
 9     y_model=knn_classifier.predict(X_test)
10     #把运行结果与测试结果进行对比
11     print(accuracy_score(y_test,y_model))        

3.3 score 方法

在回归模型当中，由于测试结果并非固定值，所以一般通过使用 score(self, X, y, sample_weight=None) 方法，通过对 R^2（判定系数）来衡量与目标均值的对比结果。
R^2=1，则表示模型与数据完成吻合，如果R^2为负值，侧表示模型性能非常差。

1     X,y=make_wave(1000)
2     X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
3     linearReg=LinearRegression()
4     linearReg.fit(X_train,y_train)
5     print(linearReg.score(X_train,y_train))

3.4 validation_curve 验证曲线

上一节曾经讲过，要提高模型的质量，应该在过拟合跟欠拟合当中，选择一个平衡点。
有见及此，为了更直观地了解模型的质量，sklearn 特意准备了 validation_curve 方法 ，可以更直观与观察到验证曲线的示意图。

validation_curve(estimator, X, y, *, param_name, param_range, groups=None, 
　　   cv=None, scoring=None, n_jobs=None, pre_dispatch="all",
　　   verbose=0, error_score=np.nan, fit_params=None)

• estimator：实现了fit 和 predict 方法的对象
• X : 训练的向量
• y : 目标相对于X分类或回归
• param_name:将被改变的变量名称
• param_range:param_name对应的变量的取值
• cv:如果传入整数，测试数据将分成对应的分数，其中一份作为cv集，其余n-1作为traning（默认为3份）

只需要简单地绑定模型，输入数据，便可得到模型的准确率变化曲线

 1     # validation_curve 绑定 SVC
 2     X, y = load_digits(return_X_y=True)
 3     param_range = np.logspace(-6, -1, 5)
 4     train_scores, test_scores = validation_curve(
 5         SVC(), X, y, param_name="gamma", param_range=param_range,
 6         scoring="accuracy", n_jobs=1)
 7     #训练数据与测试数据的平均得分
 8     train_scores_mean = np.mean(train_scores, axis=1)
 9     test_scores_mean = np.mean(test_scores, axis=1)
10     #显示数据
11     plt.title("Validation Curve with SVM")
12     plt.xlabel(r"$\gamma$")
13     plt.ylabel("Score")
14     plt.ylim(0.0, 1.1)
15     lw = 2
16     plt.semilogx(param_range, train_scores_mean, label="Training score",
17                  color="darkorange", lw=lw)
18     plt.semilogx(param_range, test_scores_mean, label="Cross-validation score",
19                  color="navy", lw=lw)
20     plt.legend(loc="best")
21     plt.show()

运行结果

下面的章节开始介绍  sklearn 中监督学习的一些常用模型，可能模型的使用方法基本一致，看起来似乎千篇一律。实则不然，因为机器学习与一般的开发不一样，主要是了解不同模型的运算规则和适用场景。从原理中理解实质，希望读者能够明白。

四、线性模型

线性模型是实践中应用最为广泛的模型之一，它支持分类与回归，最常用的线性分类算法有 LogisticRegression , LinearSVC、SGDClassifier，常用的线性回归算法有 LinearRegression、Ridge、Lasso 、SGDRegressor 等，后面将一一讲解。前几节，将从最常用的线性回归开始入手，介绍几个最常用的线性模型。

从最简单的直线函数 y = w * x + k 开始介绍，这就是线性模型当中最简单的单一特征模型，模型训练的目标是通过数据计算出最接近数据点的模型参数 w 与 k。
其中 x 是输入变量，也是唯一的特征;
w 为斜率，也被称为权重被保存在 coef_ 属性当中;
k 为载矩也称偏移量，被保存于 intercept_ 属性当中。
线性函数的运算结果类似于下图，是一条 斜率为 w，偏移量为 k 的直线

 

模型看似简单，然而在机器学习中模型往往是由浅入深，当输入特征由一个变为两个时，模型变会从一条直线变为一个平面，当特征变为三个时，模型将变成一个立体三维空间 ......

由此可得，线性模型的最终公式如下，模型会有 n+1 个特征

y = w[0] * x[0] + w[1] * x[1] + w[2] * x[2] + w[3] * x[3] + ...... + w[n] * x[n] + k

为了更好地理解线性模型，下面先由最简单的 “线性回归 LinearRegression” 开始讲起

4.1 线性回归 LinearRegression

LinearRegression 是最简单的的线性模型，此模型就是通过第二节介绍的最小二乘法，找出参数 w 与 k，使得训练集与预测集的均方误差 MSE 最小，最终确定 w 与 k 值。
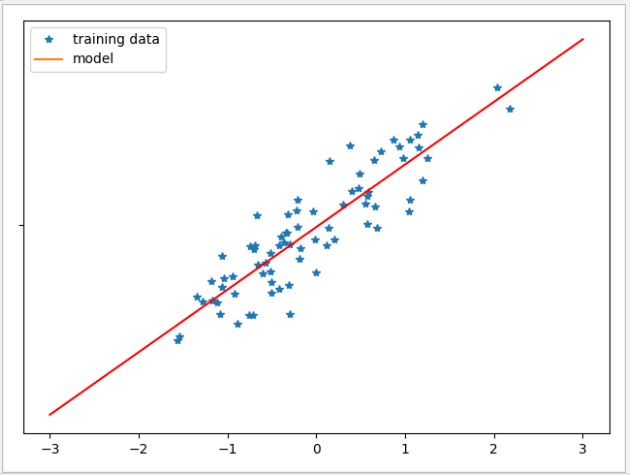
下面就是一个单一特征的数据集进行测试，用 100 条数据计算出斜率和偏移量，再划出此直线。 

 1 def linear_regression_test():
 2     #测试数据
 3     line=np.linspace(-3,3,50)
 4     datasets.make_regression(n_features=1,noise=35，random_state=1)
 5     X_train,X_test,y_train,y_test=train_test_split(X,y)
 6     #线性回归模型训练
 7     linear=LinearRegression()
 8     linear.fit(X_train,y_train)
 9     #准确率
10     print('train data prec:'+str(linear.score(X_train,y_train)))
11     print('test data prec:'+str(linear.score(X_test,y_test)))
12     #斜率与截距
13     print('coef:'+str(linear.coef_))
14     print('intercept:'+str(linear.intercept_))
15     #图形显示
16     plt.plot(X_train,y_train,'*','')
17     result=linear.predict(line.reshape(-1,1))
18     plt.plot(line,result,'r')
19     plt.legend(['training data','model'])
20     plt.show()

输出结果

线性模型

LinearRegression 模型比较简单，不需要任何参数，但因此也无法调节模型的复杂程度，可以看到训练数据与测试数据的准确都不高。在实际应用中，LinearRegression 模型的应用场景并不多。

4.2 Ridge 岭回归

为了提高准确率，sklearn 设计了 Ridge 岭回归模型来代替 LinearRegression。岭回归也是使用最小二乘法进行计算，然而与 LinearRegression 不同的是岭回归使用了正则化 L2，它会让 w 的元素尽量偏向于0。
Ridge 构造函数

1 class Ridge(MultiOutputMixin, RegressorMixin, _BaseRidge):
2     @_deprecate_positional_args
3     def __init__(self, alpha=1.0, *, fit_intercept=True, normalize=False,
4                  copy_X=True, max_iter=None, tol=1e-3, solver="auto",
5                  random_state=None):
6     ......

参数说明

• alpha 是正则项系数，初始值为1，数值越大，则对复杂模型的惩罚力度越大。
• fit_intercept：bool类型，默认为True，表示是否计算截距 ( 即 y=wx+k 中的 k )。
• normalize：bool类型，默认为False，表示是否对各个特征进行标准化(默认方法是：减去均值并除以L2范数)，推荐设置为True。如果设置为False，则建议在输入模型之前，手动进行标准化。当fit_intercept设置为False时，将忽略此参数。
• copy_X：默认值为True，代表 x 将被复制，为 False 时，则 x 有可能被覆盖。
• max_iter：默认值为None，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。
• tol：默认为小数点后3位，代表求解方法精度
• solver：求解优化问题的算法，默认值 auto，可以根据数据类型选择最合适的算法。可选的算法有：

1).svd:采用奇异值分解的方法来计算。

2).cholesky:采用scipy.linalg.solve函数求得闭式解。

3).sparse_cg:采用scipy.sparse.linalg.cg函数来求取最优解。

4).lsqr:使用scipy.sparse.linalg.lsqr求解，它是最快的。

5).sag:使用随机平均梯度下降，当n_samples和n_features都较大时，通常比其他求解器更快。

• random_state：随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。

Ridge 使用了 L2 正则化规范，对模型系数 w 进行约束，使每个特征的 w 尽可能的小，避免过度拟合。 相比 LinearRegression ，可见 Ridge 使用 L2 正则化规范后，分数有进一步的提升。

 1 def ridge_test():
 2     #测试数据
 3     line=np.linspace(-3,3,100)
 4     X,y=datasets.make_regression(n_features=1,noise=35,random_state=1)
 5     X_train,X_test,y_train,y_test=train_test_split(X,y)
 6     #岭回归模型
 7     ridge=Ridge(alpha=1)
 8     ridge.fit(X_train,y_train)
 9     #计算准确率
10     print('train data prec:'+str(ridge.score(X_train,y_train)))
11     print('test data prec:'+str(ridge.score(X_test,y_test)))
12     #斜率与截距
13     print('coef:'+str(ridge.coef_))
14     print('intercept:'+str(ridge.intercept_))
15     # 图形显示
16     plt.plot(X_train, y_train, '*', '')
17     plt.legend(['training data', 'model'])
18     result = ridge.predict(line.reshape(-1, 1))
19     plt.plot(line, result, 'r')
20     plt.show()

运算结果

 Ridge 模型

除此以外，Ridge 模型还提供了一个参数 alpha 用于控制其泛化性能，alpha 默认值为 1。
alpha 越大，w 会更趋向于零，因此泛化性能越高，但训练集上的性能会降低，在数据量较大的时候需要权衡利弊。
alpha 越小，w 的限制就会越小，训练集上的性能就会越高。要注意的是如果把 alpha 调到接近于 0，那 L2 正则化基本不起作用，Ridge 的计算结果将接近于 LinearRegression。
下面试着把 alpha 值调为 0.2 ，可以看到测试集上的分数有一定提升。 

 4.3 Lasso 模型

Lasso 跟 Ridge 一样都是线性回归模型，两者的主要区别在 Ridge 默认是使用 L2 正则化，而 Lasso 使用的是 L1 正则化规范。L1 会把参数控制趋向于0，从而抽取更有关键代表性的几个特征。
Lasso的构造函数

 1 class Lasso(ElasticNet):
 2     @_deprecate_positional_args
 3     def __init__(self, alpha=1.0, *, fit_intercept=True, normalize=False,
 4                  precompute=False, copy_X=True, max_iter=1000,
 5                  tol=1e-4, warm_start=False, positive=False,
 6                  random_state=None, selection='cyclic'):       ......

参数说明

• alpha 是正则项系数，初始值为1，数值越大，则对复杂模型的惩罚力度越大。
• fit_intercept：bool类型，默认为True，表示是否计算截距(即y=wx+k中的k)。
• normalize：bool类型，默认为False，表示是否对各个特征进行标准化(默认方法是：减去均值并除以L2范数)，推荐设置为True。如果设置为False，则建议在输入模型之前，手动进行标准化。当fit_intercept设置为False时，将忽略此参数。
• precompute：默认值为 Falise，表示是否使用预计算的 Gram 矩阵来加速计算。如果设置为 auto 代表让计算机来决定。Gram 矩阵也可以作为参数传递。对于稀疏输入这个选项总是正确的，用于保持稀疏性。
• copy_X：默认值为True，代表 x 将被复制，为 False 时，则 x 有可能被覆盖。
• max_iter：默认值为10000，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。
• tol：默认为小数点后 4 位，代表求解方法精度。
• warm_start：默认值为 False，当设置为True时，重用之前调用的解决方案作为初始化，否则，只需要删除前面的解决方案。
• positive：默认值为 False，当设置为 True 时，则系数总是为正数。
• random_state：随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。
• selection：默认值为 cyclic ，如果设置为 random，则每一次迭代都会更新一个随机系数，而不是在默认情况下按顺序循环，这样做通常会导致更快的收敛速度，尤其是当tol大于1e-4时。

Lasso 模型当中包含两个主要参数：
alpha 默认值为 1 ，按照 L1的正则化规范，alpha 值越大，特征提取数越少，更多的权重会接近于0，alpha 越小，特征提取越多，当alpha 接近于0时，Lasso 模型与 Ridge 类似，所有特征权重都不为 0
max_iter  默认值为10000， 它标志着运行迭代的最大次数，有需要时可以增加 max_iter 提高准确率。

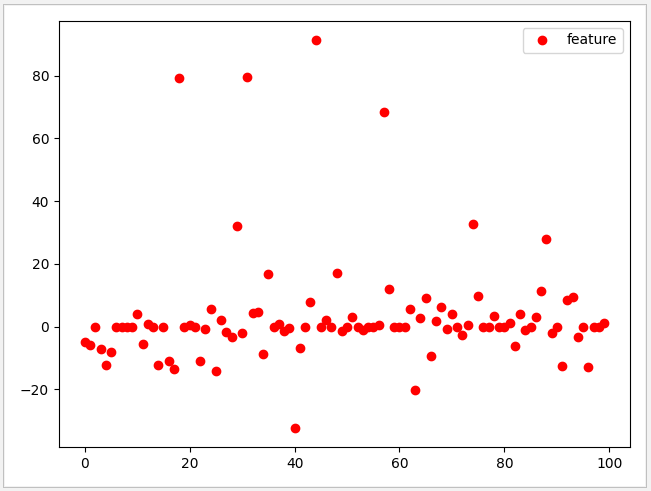
下面尝试对 100 特征的数据进行测试，把 alpha 值设置为 0.2，可以看到测试数据的准确率比较低，只有 0.82，有效的特征有72个。

 1 def lasso_test():
 2     # 测试数据
 3     X,y=datasets.make_regression(n_features=100,noise=40,random_state=1)
 4     X_train,X_test,y_train,y_test=train_test_split(X,y,train_size=0.75,test_size=0.25)
 5     # 把alpha设置为30
 6     lasso=Lasso(alpha=0.2,max_iter=10000)
 7     lasso.fit(X_train,y_train)
 8     #输出正确率
 9     print('lasso\n train data:{0}'.format(lasso.score(X_train,y_train)))
10     print(' test data:{0}'.format(lasso.score(X_test,y_test)))
11     #有效特征数与总数
12     print(' used features: {0}'.format(sum(lasso.coef_!=0)))
13     print(' total features: {0}'.format(lasso.n_features_in_))
14     plt.plot(lasso.coef_,'o',color='red')
15     plt.legend(['feature'])
16     plt.show()

运行结果

 

 试着把 alpha 调为2，此时有效特征下降到 45，而测试数据的分数达到 0.94

 

4.4 浅谈正则化概念

通过 Ridge 与 Lasso 的例子，相信大家对正则化概念会有一定的了解。在这里简单介绍一下L1、L2 正则化的区别。
正则化（Regularization）是机器学习中一种常用的技术，其主要目的是控制模型复杂度，减小过拟合。最基本的正则化方法是在原目标函数 中添加惩罚项，对复杂度高的模型进行“惩罚”。
L1 正则化则是以累加绝对值来计算惩罚项，因此使用 L1 会让 W(i) 元素产生不同量的偏移，使某些元素为0，从而产生稀疏性，提取最有效的特征进行计算。
L2 正则化则是使用累加 W 平方值计算惩罚项，使用 L2 时 W(i) 的权重都不会为0，而是对每个元素进行不同比例的放缩。 

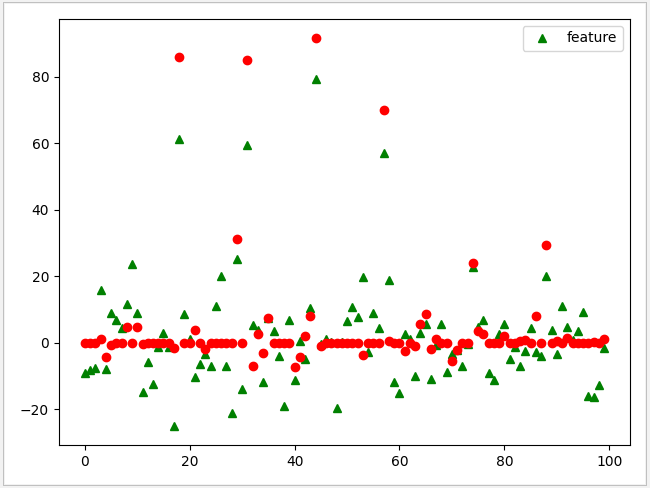
通过 Ridge 与 Lasso 对比 L1 与 L2 的区别

 1 def ridge_test():
 2     #测试数据
 3     line=np.linspace(-3,3,100)
 4     X,y=datasets.make_regression(n_features=100,noise=40,random_state=1)
 5     X_train,X_test,y_train,y_test=train_test_split(X,y)
 6     #岭回归模型
 7     ridge=Ridge()
 8     ridge.fit(X_train,y_train)
 9     #计算准确率
10     print('ridge\n  train data:{0}'.format(ridge.score(X_train,y_train)))
11     print('  test data:'.format(ridge.score(X_test,y_test)))
12     print('  used features: {0}'.format(sum(ridge.coef_!=0)))
13     print('  total features: {0}'.format(ridge.n_features_in_))
14     plt.plot(ridge.coef_,'^',color='g')
15 
16 
17 def lasso_test():
18     # 测试数据
19     X,y=datasets.make_regression(n_features=100,noise=40,random_state=1)
20     X_train,X_test,y_train,y_test=train_test_split(X,y)
21     # 把alpha设置为2
22     lasso=Lasso(alpha=2,max_iter=10000)
23     lasso.fit(X_train,y_train)
24     #输出正确率
25     print('lasso\n  train data:{0}'.format(lasso.score(X_train,y_train)))
26     print('  test data:{0}'.format(lasso.score(X_test,y_test)))
27     #斜率与截距
28     print('  used features: {0}'.format(sum(lasso.coef_!=0)))
29     print('  total features: {0}'.format(lasso.n_features_in_))
30     plt.plot(lasso.coef_,'o',color='red')
31     plt.legend(['feature'])
32 
33 ridge_test()
34 lasso_test()
35 plt.show()

运行结果

可见 Ridge 模型中有效特征仍为100，而 Lasso 的有效特征仅为 48。在一般运算中，往往会优先使用 Ridge 模型。但当数据的特征数太多时，Lasso 更显出其优势。  

4.5 SGDRegressor 模型

前面介绍的 LinearRegression、Ridge、Lasso 等几个模型，都是使用最小二乘法和求逆运算来计算参数的，下面介绍的 SGDRegressor 模型是使用梯度下降法进行计算的。
在第二节已经使用基础的 Python 代码实现最简单的梯度下降法算法，但其实在 sklearn 模型中早已准备了 SGDRegressor 模型支持梯度下降计算，运算时它比最小二乘法和求逆运算更加快节，当模型比较复杂，测试数据较大时，可以考虑使用 SGDRegressor 模型。
SGDRegressor 构造函数

1 class SGDRegressor(BaseSGDRegressor):
2     @_deprecate_positional_args
3     def __init__(self, loss="squared_loss", *, penalty="l2", alpha=0.0001,
4                  l1_ratio=0.15, fit_intercept=True, max_iter=1000, tol=1e-3,
5                  shuffle=True, verbose=0, epsilon=DEFAULT_EPSILON,
6                  random_state=None, learning_rate="invscaling", eta0=0.01,
7                  power_t=0.25, early_stopping=False, validation_fraction=0.1,
8                  n_iter_no_change=5, warm_start=False, average=False):
9      ......

• loss：默认为“squared_loss”, 选择要使用的损失函数。可用的回归损失函数有：'squared_loss'、'huber'、epsilon_unsensitive'或'squared_epsilon_unsensitive'。
• penalty：默认为 L2，用于指定惩罚项中使用的规范，可选参数为 L1 、 L2、elasticnet
• alpha：默认值为 0.0001 乘以正则项的常数。值越大，正则化越强。当学习率设为“optimal”时，用于计算学习率。
• l1_ratio：默认值为 0.15 弹性净混合参数，0 <= l1_ratio <= 1. l1_ratio=0对应于L2惩罚，l1_ratio=1到 l1。仅当 penalty 为 elasticnet 时使用。
• fit_intercept：bool类型，默认为True，表示是否计算截距 ( 即 y=wx+k 中的 k )。
• max_iter：默认值为 1000，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。
• tol：默认值为1e-3,默认为小数点后 3 位，代表求解方法精度
• shuffle：默认值为 True ，是否在每个epoch之后对训练数据进行洗牌。
• verbose：默认值为 0 详细程度。
• epsilon：当 loss 选择 “huber” 时，它决定了一个阈值，在这个阈值下，预测值将被忽略。若选择 “epsilon-insensitive” 表示若当前预测和正确标签之间的差异小于此阈值，将被忽略。
• random_state：默认值为None 随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。
• learning_rate：学习率，默认值为 ’invscaling’ ,可选 constant、optimal、invscaling、adaptive

　　　　1）‘constant’: eta = eta0；

　　　　2）‘optimal: eta = 1.0 / (alpha * (t + t0)) ;

　　　　3）‘invscaling’: eta = eta0 / pow(t, power_t);

　　　　4）‘adaptive’: eta = eta0

• eta0：默认值为0.01，初始学习速率。
• power_t：默认值为0.25 反向缩放学习速率的指数
• early_stopping：默认值为 False 验证分数没有提高时，是否使用提前停止终止培训。如果设置为True，它将自动将训练数据的分层部分作为验证，并且当分数方法返回的验证分数对 n_iter_no_change 连续时间段没有至少提高tol时终止训练。
• validation_fraction：默认值为 0.1 作为早期停机验证设置的培训数据的比例。必须介于0和1之间。仅在“早停”为真时使用。
• n_iter_no_change：默认值为 5 在提前停止之前没有改进的迭代次数。
• warm_start：bool, 默认值为 False 当设置为True时，将上一个调用的解决方案重用为fit作为初始化，否则，只需删除以前的解决方案。
• average：默认值为 False 当设置为True时，计算所有更新的 averaged SGD权重，并将结果存储在coef_ 属性中。如果设置为大于1的整数，则当看到的样本总数达到平均值时，将开始平均。所以average=10将在看到10个样本后开始平均。

SGDRegressor 模型与 Ridge 类似，默认使用 L2 正则化，所有特征权重都不为 0 而是对每个元素进行不同比例的放缩。 
max_iter  默认值为1000， 它标志着运行迭代的最大次数，有需要时可以增加 max_iter 提高准确率。
从第二节的例子可以理解，SGD默认使用 squared_loss 均方误差作为损失函数，参数 eta0 =0.01 是初始的学习速率，当 learning_rate 为 constant 时，学习速率则恒定为 0.01，若使用默认值 invscaling，学习速率则通过公式 eta = eta0 / pow(t, power_t) 计算。
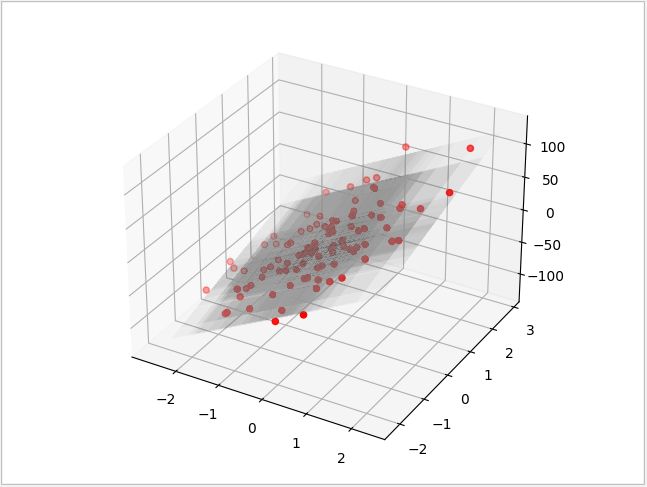
在下面的例子，把学习率设为恒定的 0.001，然后使用二个特征的数据进行测试，最后使用三维图形把计算出来的结果进行显示

 1 def sgd_regressor_test():
 2     # 测试数据
 3     X,y=dataset.make_regression(n_samples=100,n_features=2)
 4     X_train, X_test, y_train, y_test = train_test_split(X, y)
 5     # SGD 模型
 6     sgd = SGDRegressor(learning_rate='constant',eta0=0.001,average=True)
 7     sgd.fit(X_train,y_train)
 8     # 准确率
 9     print('SGD:\n  train data:{0}\n  test data:{1}'
10         .format(sgd.score(X_train,y_train),sgd.score(X_test,y_test)))
11     ax=plt.axes(projection='3d')
12     print('  coef:{0}   intercept:{1}'.format(sgd.coef_,sgd.intercept_))
13     # 生成3维图
14     ax.scatter3D(X[:,0],X[:,1],y,color='red')
15     # 生成格网矩阵
16     x0, x1 = np.meshgrid(X[:,0], X[:,1])
17     z = sgd.coef_[0] * x0 + sgd.coef_[1] * x1+sgd.intercept_
18     # 绘制3d
19     ax.plot_surface(x0, x1, z,color='white',alpha=0.01)
20     plt.show()

运行结果

 

对大数据进行测试时，相比起最小二乘法，使用梯度下降法效率会更高。下面的例子就是分别使用 LinearRegrssion 与 SGDRegressor 对 100 个特征的 100000 条数据进行测试，结果 SGD 节省了大约 30%的时间。

 1 def linear_regression_test():
 2     # 测试数据
 3     X, y = dataset.make_regression(n_samples=100000,n_features=100, random_state=2)
 4     X_train, X_test, y_train, y_test = train_test_split(X, y)
 5     # 线性回归模型训练
 6     linear = LinearRegression()
 7     linear.fit(X_train, y_train)
 8     # 准确率
 9     print('Linear:\n  train data:{0}\n  test data:{1}'
10           .format(linear.score(X_train,y_train),linear.score(X_test,y_test)))
11 
12 def sgd_regressor_test():
13     # 测试数据
14     X,y=dataset.make_regression(n_samples=100000,n_features=100,random_state=2)
15     X_train, X_test, y_train, y_test = train_test_split(X, y)
16     # SGD 模型
17     sgd = SGDRegressor(learning_rate='constant',eta0=0.01)
18     sgd.fit(X_train,y_train)
19     # 准确率
20     print('SGD:\n  train data:{0}\n  test data:{1}'
21         .format(sgd.score(X_train,y_train),sgd.score(X_test,y_test)))
22 
23 print('  Utime:{0}'.format(timeit.timeit(stmt=linear_regression_test, number=1)))
24 print('  Utime:{0}'.format(timeit.timeit(stmt=sgd_regressor_test, number=1)))

运行结果

4.6 LogisticRegression 模型

上面几个例子，都是讲述线性回归，下面将开始介绍线性分类的模型。LogisticRegression 模型虽然名称里包含了 Regression ，但其实它是一个线性分类模型。
LogisticRegression 的构造函数

 1 class LogisticRegression(LinearClassifierMixin,
 2                          SparseCoefMixin,
 3                          BaseEstimator):
 4 　　　　 @_deprecate_positional_args   
 5  　　　　def __init__(self, penalty='l2', *, dual=False, tol=1e-4, C=1.0,
 6                  fit_intercept=True, intercept_scaling=1, class_weight=None,
 7                  random_state=None, solver='lbfgs', max_iter=100,
 8                  multi_class='auto', verbose=0, warm_start=False, n_jobs=None,
 9                  l1_ratio=None):
10         ......

参数说明

• penalty：默认为 L2，用于指定惩罚项中使用的规范，可选参数为 L1 和 L2。
• dual：默认为False，对偶或原始方法。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
• tol：默认为小数点后 4 位，代表求解方法精度。
• C：正则化系数 λ 的倒数，float类型，默认为1.0，越小的数值表示越强的正则化。
• fit_intercept：bool类型，默认为True，表示是否计算截距 ( 即 y=wx+k 中的 k )。
• intercept_scaling：float类型，默认为1，仅在 solver 为 ”liblinear”，且 fit_intercept设置为True时有用 。
• class_weight：用于标示分类模型中各种类型的权重，默认值为None，即不考虑权重。也可选择balanced 让类库自己计算类型权重，此时类库会根据训练样本量来计算权重，某种类型样本量越多，则权重越低，样本量越少，则权重越高。或者输入类型的权重比，例如 class_weight={0:0.9, 1:0.1}，此时类型0的权重为90%，而类型1的权重为10%。
• random_state：随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。
• solver：求解优化算法，默认值 lbfgs，可以根据数据类型选择最合适的算法。可选的算法有：

　　　　1）liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。

　　　　2）lbfgs：利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

　　　　3）newton-cg：利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

　　　　4）sag：即随机平均梯度下降，是梯度下降法的变种，每次迭代仅仅用一部分的样本来计算梯度，适合数据量较大时使用。

　　　　5）saga：线性收敛的随机优化算法的的变重。

• max_iter：默认值为 100，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。
• multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。 
• verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。
• warm_start：默认值为 False，当设置为True时，重用之前调用的解决方案作为初始化，否则，只需要删除前面的解决方案。
• n_jobs：CPU 并行数，默认为None，代表1。若设置为 -1 的时候，则用所有 CPU 的内核运行程序。
• l1_ratios ： 默认为None，表示弹性网混合参数列表。

LogisticRegression 包含两个最常用的参数 penalty 正则化规则、C 正则化程度，由构造函数可以看到，一般情况下 LogisticRegression 使用的是 L2 正则规范。此时决定正则化规范强度的参数是由 C 值决定，C 越大，对应的正则化越弱，数据集的拟合度会更高，C 越小，则模型的权重系统 w 更趋向于 0。

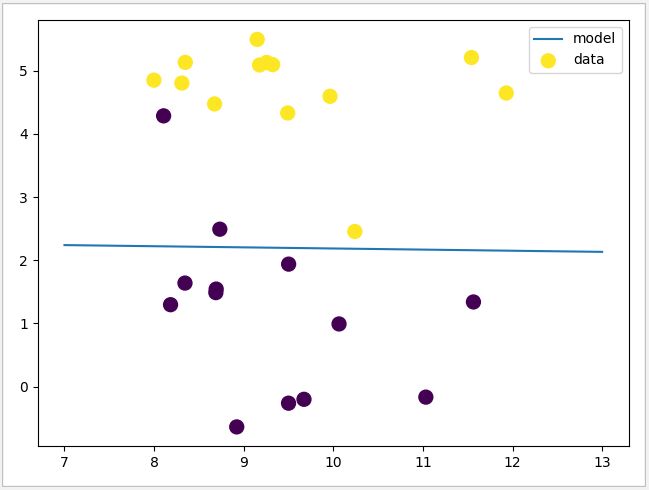
最典型的例子就是使用 make_forge 库里的例子进行测试

 1 def logistic():
 2     #生成数据集
 3     X,y=datasets.make_forge()
 4     X_train,X_test,y_train,y_test=train_test_split(X,y)
 5     #对Logistic模型进行训练
 6     logistic=LogisticRegression(C=1.0,random_state=1)
 7     logistic.fit(X_train,y_train)
 8     #输入正确率
 9     print('logistic\n  train data:{0}'.format(logistic.score(X_train,y_train)))
10     print('  test data:{0}'.format(logistic.score(X_test,y_test)))
11     #输出模型决策边界
12     line = np.linspace(7, 13, 100)
13     plt.scatter(X[:,0], X[:,1],c=y,s=100)
14     plt.legend(['model','data'])
15     plt.show()

运行结果

 

此时，虽然测试数据集比较简单，但仍可见类型为0和1的数据仍有产生一定的错位。此时，尝试将参数 C 调整为 100，得出的结果如下图。
可见，当C值越大时，正则化规则越弱，数据集的拟合度会更高

 

 相反，若将 C 调整为 0.01 时，权重系数 w 会越趋向于0，它会让公式适用于更多的数据点

 

 

LogisticRegression 除了可以通过 C 控制其正则化强度外，还可以通过 penalty 参数选择正则化规则，penalty 默认值为 L2，但是当数据集的特征较多时，可以尝试通过设置 penalty 让其使用 L1 正则化。但需要注意的是，当使用 L1 正则化时 solver 必须使用 liblinear 算法，否则系统会报错。

 1 def logistic(penalty,c):
 2     #生成数据集
 3     X,y=dataset.make_classification(n_samples=1000,n_features=100,random_state=1)
 4     X_train,X_test,y_train,y_test=train_test_split(X,y)
 5     #对Logistic模型进行训练
 6     if(penalty=='l1'):
 7         solver='liblinear'
 8     else:
 9         solver='lbfgs'
10     logistic=LogisticRegression(penalty=penalty,C=c,solver=solver,random_state=1)
11     logistic.fit(X_train,y_train)
12     #输入正确率
13     print('{0}\n  train data:{1}'.format(penalty,logistic.score(X_train,y_train)))
14     print('  test data:{0}'.format(logistic.score(X_test,y_test)))
15 
16     #输出模型决策边界
17     print('  total features:{0}'.format(logistic.n_features_in_))
18     print('  used features:{0}'.format(sum(logistic.coef_[0]!=0)))
19     plt.plot(logistic.coef_[0],'^')
20 logistic('l1',0.2)
21 logistic('l2',0.2)
22 plt.show()

运行结果

可以看到当使用 L1 规则时，系统只使用了 4 个特征，此方法更适用于特征数量比较多的数据集。
使用 L2 时 C 值为 0.2，系统使用了100个特征，由特征图形可见，其权重系数 w 都接近于 0

此时可尝试调节一下参数，对比一下运行 L2 ，输入不同 C 值时的变化。

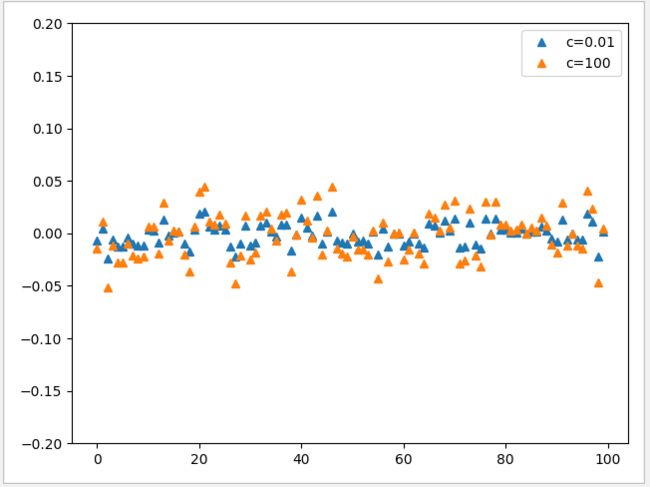
1 logistic("l2", 0.01)
2 logistic('l2',100)
3 plt.legend(['c=0.01','c=100'])
4 plt.show()

运行结果

 可见 C 值越小，w 就会越趋向于0，C 值越大，w 就会越分散且受正则化的约束越小

4.7 LinearSVC 线性支持向量机

上面的例子所看到的线性分类模型，大部分的例子都只二分类的，下面介绍一下可用于多分类的线性模型 LinearSVC 
LinearSVC 的构造函数

1 class LinearSVC(LinearClassifierMixin,
2                 SparseCoefMixin,
3                 BaseEstimator):
4     @_deprecate_positional_args
5     def __init__(self, penalty='l2', loss='squared_hinge', *, dual=True,
6                  tol=1e-4, C=1.0, multi_class='ovr', fit_intercept=True,
7                  intercept_scaling=1, class_weight=None, verbose=0,
8                  random_state=None, max_iter=1000):
9         ......

参数说明

• penalty：默认为 L2，用于指定惩罚项中使用的规范，可选参数为 L1 和 L2。当使用 L1 准则时，参数 loss 必须为 squared_hinge , dual 必须为 False。
• loss : 指定损失函数，默认值为 squared_hinge，可选择 ‘hinge’ 或 ‘squared_hinge’ 。
• dual：默认为False，对偶或原始方法。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
• tol：默认为小数点后 4 位，代表求解方法精度。
• C：正则化系数 λ 的倒数，float类型，默认为1.0，越小的数值表示越强的正则化。
• multi_class : 默认值为 ovr，可选择 ‘ovr’ 或 ‘crammer_singer’ ，用于确定多类策略。 “ovr” 训练n_classes one-vs-rest 分类器，而 “crammer_singer” 优化所有类的联合目标。  如果选择“crammer_singer”，则将忽略选项 loss，penalty 和 dual 参数。
• fit_intercept：bool类型，默认为True，表示是否计算截距 ( 即 y=wx+k 中的 k )。
• intercept_scaling：float类型，默认为1，仅在 fit_intercept设置为True时有用 。
• class_weight：用于标示分类模型中各种类型的权重，默认值为None，即不考虑权重。也可选择balanced 让类库自己计算类型权重，此时类库会根据训练样本量来计算权重，某种类型样本量越多，则权重越低，样本量越少，则权重越高。或者输入类型的权重比，例如 class_weight={0:0.9, 1:0.1}，此时类型0的权重为90%，而类型1的权重为10%。
• verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出
• random_state：随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。
• max_iter：默认值为 10000，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。

与LogisticRegression相似，LinearSVC 默认也是使用 L2 准则，同样可以通过 C 控制其正则化强度，C 越大，对应的正则化越弱，数据集的拟合度会更高，C 越小，则模型的权重系统 w 更趋向于 0。
还可以通过 penalty 参数选择正则化规则，当使用 L1 准则时，参数 loss 必须为 squared_hinge , dual 必须为 False。

当用于多个类别时，LinearSVC 会使用一对其余的方式，每次学习都会使用一个二分类模型，然后把余下的数据集再次进行二分类，不断循环最后得出预测结果。

 1 def linearSVC():
 2     #生成数据集    
 3     X,y=mglearn.datasets.make_blobs(n_samples=200,random_state=23,centers=3)
 4     X_train,X_test,y_train,y_test=train_test_split(X,y)
 5     #使用 LinearSVC 模型，使用 L1 准则
 6     linearSVC=LinearSVC(penalty='l1',loss='squared_hinge', dual=False)
 7     linearSVC.fit(X_train,y_train)
 8     #输出准确率
 9     print('LinearSVC\n  train data:{0}'.format(linearSVC.score(X_train,y_train)))
10     print('  test data:{0}'.format(linearSVC.score(X_test,y_test)))
11     #划出图形分隔线
12     plt.scatter(X[:,0], X[:,1],c=y,s=100,cmap='autumn',marker='*')
13     n=np.linspace(-8,8,100)
14     value0=(-n*linearSVC.coef_[0][0] - linearSVC.intercept_[0]) / linearSVC.coef_[0][1]
15     value1=(-n*linearSVC.coef_[1][0] - linearSVC.intercept_[1]) / linearSVC.coef_[1][1]
16     value2=(-n*linearSVC.coef_[2][0] - linearSVC.intercept_[2]) / linearSVC.coef_[2][1]
17     plt.plot(n.reshape(-1, 1), value0,'-')
18     plt.plot(n.reshape(-1, 1), value1,'--')
19     plt.plot(n.reshape(-1, 1), value2,'+')
20     plt.legend(['class0','class1','class2'])
21     plt.show()

运行结果

 4.8 SGDClassifier 分类模型

SGDClassifier 与 SGDRegressor 类似，都是使用梯度下降法进行分类计算，由于SGD是以一次一个的方式独立处理训练实例，所以它能够有效处理大型的数据集。SDGClassifier 默认也是使用 L2 准则，注意与SGDRegressor不同的是它的学习率 learning_rate 默认使用 optimal，此时 eta0 无效，若要使用 eta 0 需要提前修改 learning_rate 参数。

构造函数

 1 class SGDClassifier(BaseSGDClassifier):
 2     @_deprecate_positional_args
 3     def __init__(self, loss="hinge", *, penalty='l2', alpha=0.0001,
 4                  l1_ratio=0.15,
 5                  fit_intercept=True, max_iter=1000, tol=1e-3, shuffle=True,
 6                  verbose=0, epsilon=DEFAULT_EPSILON, n_jobs=None,
 7                  random_state=None, learning_rate="optimal", eta0=0.0,
 8                  power_t=0.5, early_stopping=False, validation_fraction=0.1,
 9                  n_iter_no_change=5, class_weight=None, warm_start=False,
10                  average=False):
11     ......

• loss：默认为“hinge”, 选择要使用的损失函数。可用的损失函数有：'hinge', 'log', 'modified_huber','squared_hinge', 'perceptron'。log 损失使逻辑回归成为概率分类器。 'modified_huber'是另一个平滑的损失，它使异常值和概率估计具有一定的容忍度。“ squared_hinge”与hinge类似，但会受到二次惩罚。“perceptron”是感知器算法使用的线性损失。
• penalty：默认为 L2，用于指定惩罚项中使用的规范，可选参数为 L1 、 L2、elasticnet
• alpha：默认值为 0.0001 乘以正则项的常数。值越大，正则化越强。当学习率设为“optimal”时，用于计算学习率。
• l1_ratio：默认值为 0.15 弹性净混合参数，0 <= l1_ratio <= 1. l1_ratio=0对应于L2惩罚，l1_ratio=1到 l1。仅当 penalty 为 elasticnet 时使用。
• fit_intercept：bool类型，默认为True，表示是否计算截距 ( 即 y=wx+k 中的 k )。
• max_iter：默认值为 1000，部分求解器需要通过迭代实现，这个参数指定了模型优化的最大迭代次数。
• tol：默认值为1e-3,默认为小数点后 3 位，代表求解方法精度
• shuffle：默认值为 True ，是否在每个epoch之后对训练数据进行洗牌。
• verbose：默认值为 0 详细程度。
• epsilon：默认值为0.1  loss 选择 “huber” 时，它决定了一个阈值，在这个阈值下，预测值将被忽略。若选择 “epsilon-insensitive” 表示若当前预测和正确标签之间的差异小于此阈值，将被忽略。
• n_job：CPU 并行数，默认为None，代表1。若设置为 -1 的时候，则用所有 CPU 的内核运行程序。
• random_state：默认值为None 随机数种子，推荐设置一个任意整数，同一个随机值，模型可以复现。
• learning_rate：学习率，默认值为 ’optimal’ ,可选 constant、optimal、invscaling、adaptive

　　　　1）‘constant’: eta = eta0；

　　　　2）‘optimal: eta = 1.0 / (alpha * (t + t0)) ;

　　　　3）‘invscaling’: eta = eta0 / pow(t, power_t);

　　　　4）‘adaptive’: eta = eta0

• eta0：默认值为0.0，初始学习速率。当 learning_rate 为 optimal 时，此值无效。
• power_t：默认值为0.5 反向缩放学习速率的指数
• early_stopping：默认值为 False 验证分数没有提高时，是否使用提前停止终止培训。如果设置为True，它将自动将训练数据的分层部分作为验证，并且当分数方法返回的验证分数对 n_iter_no_change 连续时间段没有至少提高tol时终止训练。
• validation_fraction：默认值为 0.1 作为早期停机验证设置的培训数据的比例。必须介于0和1之间。仅在“早停”为真时使用。
• n_iter_no_change：默认值为 5 在提前停止之前没有改进的迭代次数。
• class_weight:  类别关联的权重，使用字典格式，默认值 {class_label: None} 也可选择balanced 让类库自己计算类型权重，此时类库会根据训练样本量来计算权重，某种类型样本量越多，则权重越低，样本量越少，则权重越高。或者输入类型的权重比，例如 class_weight={0:0.9, 1:0.1}，此时类型0的权重为90%，而类型1的权重为10%。
• warm_start：bool, 默认值为 False 当设置为True时，将上一个调用的解决方案重用为fit作为初始化，否则，只需删除以前的解决方案。
• average：默认值为 False 当设置为True时，计算所有更新的 averaged SGD权重，并将结果存储在coef_ 属性中。如果设置为大于1的整数，则当看到的样本总数达到平均值时，将开始平均。所以average=10将在看到10个样本后开始平均。

下面尝试用 SDGClassifier 区分MNIST的数字图片，由于图片有70000张，运行可能较慢，尝试使用多核运算，把 n_job 设置为 -1，把学习率设置为固定值 0.01，可以看到准确率可以达到将近 90%

 1 def sgd_classifier_test():
 2     # 输入入数据
 3     (X_train, y_train), (X_test, y_test)=keras.datasets.mnist.load_data()
 4     # 把28*28图像数据进行转换
 5     X_train=X_train.reshape(-1,784)
 6     X_test=X_test.reshape(-1,784)
 7     #使用SGDClassfier模式，使用多核计算,学习率为0.01
 8     sgd_classifier=SGDClassifier(learning_rate='constant',eta0=0.01,n_jobs=-1)
 9     sgd_classifier.fit(X_train,y_train)
10     #查看准确率
11     print('SGDClassfier\n  train data:{0}\n  test data:{1}'.format(
12         sgd_classifier.score(X_train,y_train)
13         ,sgd_classifier.score(X_test,y_test)))
14     #查看测试数量第256幅图
15     data=X_test[256].reshape(28,28)
16     plt.imshow(data,cmap='binary')
17     plt.show()
18     print('  test number is:{0}'.format(y_test[256]))

运行结果

 

4.9 多项式回归与管道

4.9.1 PolynomialFeatures 多项式回归模型 

到此以上所有的例子用的都是纯线性的实例，然而现实场景中并非如此，比如说一个简单的二元一次的方程  y = a*x*x+b*x+c 所构成的数据，就不可能通过直线进行进行分割。为此，sklearn 准备了多项式回归模型 PolynomialFeatures 来解决此问题。前面提到普通的线性模型每个特征都是符合单次方规则：y = w[0] * x[0] + w[1] * x[1] + w[2] * x[2] + w[3] * x[3] + ...... + w[n] * x[n] + k，每个模型会有 n+1 个特征。而PolynomialFeatures 模型每个特征可以有多次方关系: 当 degree=N 时，每个特征都会符合关系式 y = w[0]+w[1]*x+w[2]*x2+w[3]*x3+....+w[n]*xn。如此类推如果有多个特征，则

构造函数

1 class PolynomialFeatures():
2     @_deprecate_positional_args
3     def __init__(self, degree=2, *, interaction_only=False, include_bias=True,
4                  order='C'):
5         self.degree = degree
6         self.interaction_only = interaction_only
7         self.include_bias = include_bias
8         self.order = order
9         ......

• degree：默认值为2，控制多项式的次数；
• interaction_only：默认为 False，如果指定为 True，那么就不会有特征自己和自己结合的项，组合的特征中没有 X12或 X1 * X23
• include_bias：默认为 True 。如果为 True 的话，那么结果中就会有 0 次幂项，即全为 1 这一列。
• order:  默认为"C" ，可选择 "F" 。“C” 表示是在密集情况（dense case）下的输出array的顺序，“F” 可以加快操作但可能使得subsequent estimators变慢。

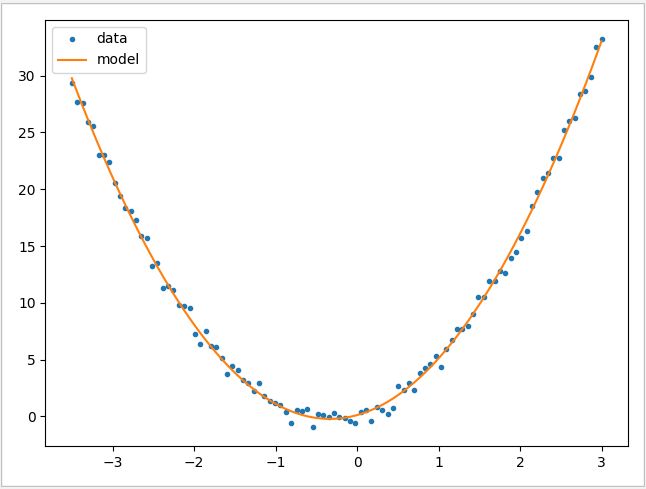
用一个二元一次的方程  y = a*x*x+b*x+c 作为例子，首先生成100 个点的测试数据画在图上，然后使用多项式回归 PolynomialFeatures 模式，把 degree 设置为默认值 2，最后使用 LinearRegression 模式根据斜率和变量画出曲线。

 1 # 测试数据，根据 y=3*x*x+2*x+1 生成
 2 def getData():
 3     x=np.linspace(-3.5,3,100)
 4     y=3*x*x+2*x+1
 5     d=np.random.random(100)*2
 6     y=y-d
 7     plt.plot(x,y,'.')
 8     return [x,y]
 9 
10 def polynomial_test():
11     # 获取测试数据
12     data=getData()
13     X=data[0].reshape(-1,1)
14     y=data[1]
15     # 生成多项式回归模型
16     polynomial=PolynomialFeatures(degree=2)
17     X_poly=polynomial.fit_transform(X)
18     # 把运算过的数据放到 LinearRegression 进行运算
19     linearRegression=LinearRegression()
20     
21     linearRegression.fit(X_poly,y)
22     # 打印数据
23     print('PolynomialFeature:\n  coef:{0}\n  intercept:{1}\n  score:{2}'
24           .format(linearRegression.coef_,linearRegression.intercept_,
25                   linearRegression.score(X_poly,y)))
26     # 根据斜率和截距画出图
27     x=np.linspace(-3.5,3,100)
28     y=linearRegression.coef_[2]*x*x+linearRegression.coef_[1]*x+linearRegression.intercept_
29     plt.plot(x,y)
30     plt.legend(['data','model'])
31     plt.show()

运行结果

 

4.9.2 Pipeline 管道

正如上一章节的例子，如果繁杂的模型每次都需要经过多个步骤运算，那将是一个耗时费力的操作，有见及此，sklearn 中有一个 Pipeline 类可以按工作流程分步骤执行模型训练。在上一章节数据先经过 PolynomialFeatures 模型训练再进行 LinearRegression 训练可写为 pipe=Pipeline([('polynomial',PolynomialFeatures()),('linearRegression',LinearRegression())]) ，在 Pipeline 参数是以字典的形式输入，先输入名称，再输入类型。如果觉得每次都要为模型对象定义参数名称比较麻烦，sklearn 还有一个更简单的方法 make_pipeline ，使用此方法只需要直接把模型的类按顺序输入即可 pipe=make_pipeline(PolynomialFeatures(),LinearRegression()) ，事实上这种写法也是管道最常用的方法。
使用 Pipeline 管道，可以把上一节的例子简化成下面的代码，输出完全一样的结果。

 1 # 测试数据根据 y=3*x*x+2*x+1 生成
 2 def getData():
 3     x=np.linspace(-3.5,3,100)
 4     y=3*x*x+2*x+1
 5     d=np.random.random(100)*2
 6     y=y-d
 7     plt.plot(x,y,'.')
 8     return [x,y]
 9 
10 def polynomial_test():
11     # 获取测试数据
12     data=getData()
13     X=data[0].reshape(-1,1)
14     y=data[1]
15     # 生成管道先执行 PolynomialFeatures 再执行 LinearRegression
16     pipe=make_pipeline(PolynomialFeatures(degree=2),LinearRegression())
17     # 训练数据
18     pipe.fit(X,y)
19     # 获取执行对象
20     linearRegression=pipe.steps[1][1]
21     # 打印数据
22     print('PolynomialFeature:\n  coef:{0}\n  intercept:{1}\n  score:{2}'
23           .format(linearRegression.coef_,linearRegression.intercept_,
24                   pipe.score(X,y)))
25     # 根据斜率和截距画出图
26     x=np.linspace(-3.5,3,100)
27     y=linearRegression.coef_[2]*x*x+linearRegression.coef_[1]*x+linearRegression.intercept_
28     plt.plot(x,y)
29     plt.legend(['data','model'])
30     plt.show()

由于篇幅关系，线性模型的使用就先介绍到这里，关于 支持向量机、k近邻、朴素贝叶斯分类 、决策树 等章节将在 《 Python 机器学习实战 —— 监督学习（下）》中详细讲述，敬请留意。

本篇总结

本文主要讲述了机械学习的相关概念与基础知识，监督学习的主要流程。对损失函数进行了基础的介绍，并对常用的均方误差与递度下降法的计算过程进行演示，希望能帮助大家更好地理解。
在线性模型方法，对常用的 LogisticRegression , LinearSVC、SGDClassifier、 LinearRegression、Ridge、Lasso 、SGDRegressor  等线性模型进行了介绍。最后对非线性的 PolynomialFeatures 多项式回归模型进行介绍，讲解管道 Pipe 的基本用法。
希望本篇文章对相关的开发人员有所帮助，由于时间仓促，错漏之处敬请点评。

对 .Python  开发有兴趣的朋友欢迎加入QQ群：790518786 共同探讨 ！
对 JAVA 开发有兴趣的朋友欢迎加入QQ群：174850571 共同探讨！
对 .NET  开发有兴趣的朋友欢迎加入QQ群：162338858 共同探讨 ！

作者：风尘浪子

https://blog.csdn.net/Leslies2/article/details/117991350

原创作品，转载时请注明作者及出处