机器学习sklearn----通过轮廓系数确定适合的n_clusters

前面的文章我们知道了KMeans的常用评估指标 轮廓系数。这篇文章我们介绍怎样通过轮廓系数来确定最佳的n_cluster

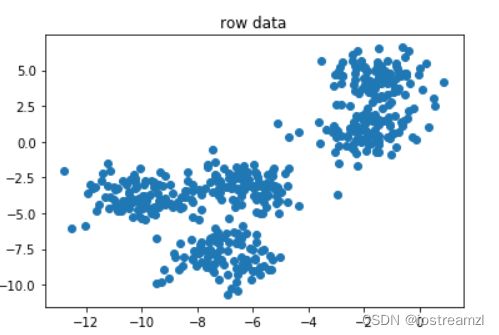
创建数据集

创建一个有5个分类的数据集，用于聚类，这里创建数据集我们是知道分类情况的，但是实际中我们是基本不会知道分类情况的。也就没有了最佳的聚类效果参考。所以需要使用到轮廓系数来选择最佳的聚类数量。

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%matplotlib inline
warnings.filterwarnings("ignore") # 忽略警告

# 创建数据集
X, y = make_blobs(n_samples = 500, n_features=2, centers=5, random_state=1)
plt.scatter(X[:, 0], X[:, 1])
plt.title("row data")

n_clusters=4详细画图代码解析

fig, charts = plt.subplots(1, 2)
# 创建一行两列的一张画布
# 返回值第一个为画布本身
# 返回值第二个为子图对象的数组

# 设置图像的大小
fig.set_size_inches(14, 5)

# 训练模型
km4 = KMeans(n_clusters=4).fit(X)
labels = km4.labels_
sil_samples = silhouette_samples(X, labels) # 计算每个样本点的轮廓系数

# 每个聚类填充之间的间隔为20
interval = 20

# 每个填充区域的上下限
lower = 0
higher = 0
for i in range(4) :
    # 将第i个聚类中的每个样本的轮廓系数取出
    sil_samples_i = sil_samples[labels == i]
    
    # 将轮廓系数排序，使得画出的图的一个弧线方便展示
    sil_samples_i.sort()
    
    # 计算填充区域的上界
    higher = sil_samples_i.shape[0] + lower
    
    # 进行填充
    charts[0].fill_betweenx(np.arange(lower, higher),
                           sil_samples_i,
                           facecolor=cm.nipy_spectral(i/4)
                           )
    
    # 显示聚类的类别
    charts[0].text(-0.05, (lower+higher) * 0.5, str(i))
    
    # 更新下界
    lower = higher + interval
    
# 画出轮廓系数的均值线
charts[0].axvline(x=sil_samples.mean(), color='red', linestyle='--')

# 设置坐标轴的显示范围
charts[0].set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1.0])
charts[0].set_yticks([])

# 画出聚类的结果散点图
charts[1].scatter(X[:, 0], X[:, 1], c=labels)

# 画出质心
centers = km4.cluster_centers_
charts[1].scatter(centers[:, 0], centers[:, 1], color='red', marker='x', s=80)

plt.show()
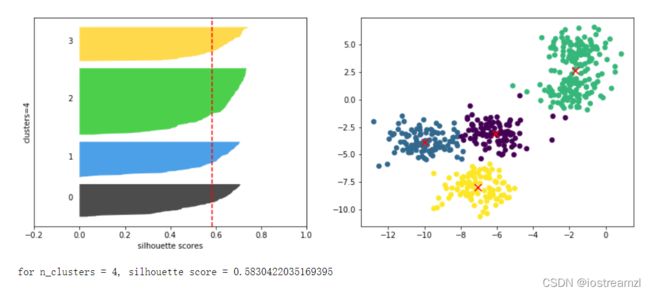
# 从图上来看每个聚类中都有较多的部分样本轮廓系数超过了平均水平
# 这说明n_clusters=4是一个比较好的聚类结果

通过上面的代码就能画出一个n_cluster对应的图了。在将上面的代码包装到一个关于n_cluster的循环中，就能实现完整的画图代码了

完整代码

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples

import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm

%matplotlib inline
warnings.filterwarnings("ignore") # 忽略警告

# 创建数据集
X, y = make_blobs(n_samples = 500, n_features=2, centers=5, random_state=1)

for n_clusters in range(2, 9) :
    # 模型训练
    km = KMeans(n_clusters=n_clusters).fit(X)
    labels = km.labels_
    sil_samples = silhouette_samples(X, labels)
    
    # 建立画布
    fig, charts = plt.subplots(1, 2)
    fig.set_size_inches(14, 5)
    
    interval = 20
    lower = 0
    higher=0
    
    for i in range(n_clusters) :
        sil_samples_i = sil_samples[labels == i]
        sil_samples_i.sort()
        higher = sil_samples_i.shape[0] + lower
        
        # 填充
        charts[0].fill_betweenx(np.arange(lower, higher),
                               sil_samples_i,
                               facecolor=cm.nipy_spectral(i/n_clusters),
                               alpha=.7)
        
        # 显示类别
        charts[0].text(-0.05, (lower + higher) * 0.5, str(i))
        
        lower = higher + interval
    
    # 画出轮廓系数的均值线
    charts[0].axvline(x=sil_samples.mean(), color='red', linestyle='--')
        
    # 设置坐标轴
    charts[0].set_xlabel("silhouette scores")
    charts[0].set_ylabel("clusters={}".format(n_clusters))
    charts[0].set_xticks(np.arange(-0.2, 1.2, 0.2))
    charts[0].set_yticks([])
    
    # 画出聚类的结果散点图
    charts[1].scatter(X[:, 0], X[:, 1], c=labels)

    # 画出质心
    centers = km.cluster_centers_
    charts[1].scatter(centers[:, 0], centers[:, 1], color='red', marker='x', s=80)
    
    plt.show()
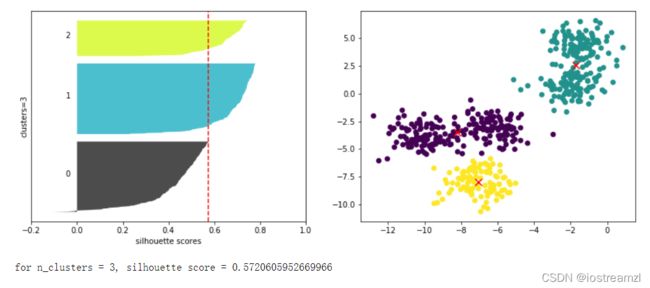
    print("for n_clusters = {}, silhouette score = {}\n".format(n_clusters, sil_samples.mean()))

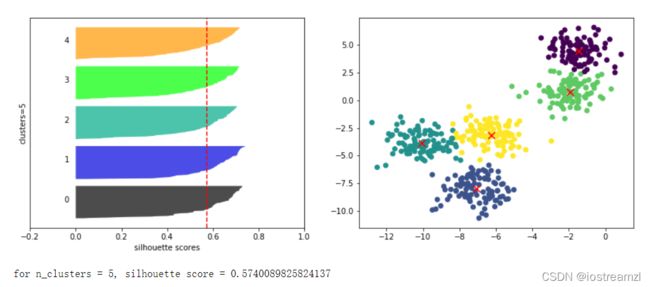
从上面的结果来看n_clusters=2的时候轮廓系数是最高的。但是从每个样本的轮廓系数来看。该聚类结果主要的贡献在第0个聚类。也就是说，第0个聚类的效果很好，但是第一个聚类效果不是很好，大部分的轮廓系数低于平均值。
在具体的应用总怎么选择需要看实际需求，需要结合人力财力来做出最佳的选择。