Opencv 笔记5 边缘处理-canny、sobel、Laplacian、Prewitt
一、边缘检测概述
边缘检测是计算视觉中的基本问题,边缘检测的目的是标识图像中亮度变换明显的点。边缘检测大幅度的减少了图像的数据量(分为两种:灰度图像边缘检测和彩色图像边缘检测),并且剔除了不相关的信息,保留了重要的结构属性。总之,图像的边缘检测是图像分割、目标区域识别和区域形状提取等图像分析的基石,也是图像中特征提取的很重要的方法。如何来实现?可以分为大的两步,一是图像边缘和背景的分离,二是 辨别出轮廓。实际的图像不像我们说的那么简单,往往是各种类型的边缘和他们模糊之后结果的结合,并且实际图像中存在着噪声,而噪声和边缘都属于高频信号。
为了得到图像轮廓清晰的图像,我们一般要进行锐化,要说锐化,就要从锐度说起,锐度其实就是边缘的对比度,锐度的提高是在不增加图像的像素的基础上造成的提高图像清晰度的假象。锐化的目的是使图像边缘、轮廓线、细节变的清晰,因为当我们去除噪声的时候源图像经过了一系列的平滑处理之后图像和边缘变的模糊,因此可以对平滑后的图像进行逆运算。锐化的方法有两种:1、高通滤波;2、空域微分法。
常见的噪声:加性噪声、乘性噪声、量化噪声
边缘的特征和分类:边缘有方向和幅度两个特征,沿着边缘方向走像素值逐渐平稳,垂直于边缘方向,像素值变化剧烈。
分类:1、阶跃性边缘,它两边的像素值有明显的差距,方向导数在边缘处是零交叉;
2、屋顶状边缘,它是从增加到减少的转折点,二阶方向导数在这里取得极致;
常见边缘检测类型:1、一阶微分边缘检测,通过计算图像的梯度值来检测图像边缘,常见的算子有Sobel 、Prewitt 、Roberts、差分算子
2、二阶微分边缘检测,求二阶导数的过零点来检测边缘,如拉普拉斯、高斯拉普拉斯、Canny
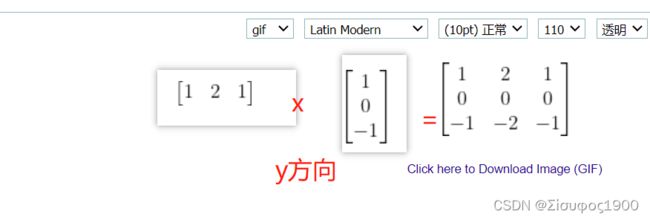
二、梯度以及边缘检测思想
如上图所示,边缘一般是以一阶导和二阶导数来检测。
术语介绍:
(1)、边缘点:灰度值显著变化的点
(2)、边缘段:边缘点坐标和方向的总和,边缘的方向可以是梯度角
(3)、轮廓:边缘列表
二阶偏导数-拉普拉斯算子数学原理
梯度以及Roberts 、Sobel 数学原理
导数总结如下:
a、一阶导数产生比较粗劣的边缘,二阶导数则比较精致,对细节的把控比较好,如细线,孤立的亮点等。
b、二阶导在灰度斜坡和台阶出会产生双边边缘响应,二阶的符号可以判断亮暗走势,和halcon 里面的双边算子是一样的。
设计到梯度的东西,后续会在PCA中详细介绍。下面是常见的几种边缘检测的详解
三、经典图像边缘检测算法
差分边缘检测
Roberts
Sobel
Prewitt
Log
Dog
Canny
Laplacian
Scharr、Kirsch、Robinson (了解)
marr-hildreth(了解)
1、 差分边缘检测
当我们处理图像的时候,可以用一阶差分来代替图像的导数,在x和y方向上各种差分得到一个x和y方向上的矩阵,还有一个是对角线的矩阵,他和x和有方向上的差分的推导过程是一样的,矩阵如下:
如何实现的先不写了,重点放在后面的几个算子上
2、 Roberts
从上面可以知道Roberts 算子的矩阵推导,Roberts 算子又被称为交叉微分算子,基于交叉差分的梯度算法(一阶导数),矩阵如下:
这个是用opencv已经集成的算子得出的结果(为了找一个能说明的图片我费了好长的时间)
src = imread("C:\\Users\\19473\\Desktop\\opencv_images\\305.jpg");
if (!src.data)
{
printf("could not load image....\n");
}
cvtColor(src, src_gray,COLOR_BGR2GRAY);
imshow("原图", src_gray);
// Robert X方向上的算子
Mat kernel = (Mat_(2, 2) << -1, 0, 0, 1);
filter2D(src_gray, dest1, -1, kernel, Point(-1, -1), 0.0);
imshow("45度", dest1);
// Robert Y方向上的算子
Mat kernel_y = (Mat_(2, 2) << 0, -1, 1, 0);
filter2D(src_gray, dest2, -1, kernel_y, Point(-1, -1), 0.0);
imshow("135度", dest2);
// 图像融合
convertScaleAbs(dest2, dest2);
convertScaleAbs(dest1, dest1);
Mat RobertImage;
addWeighted(dest1, 0.5, dest2, 0.5, 0, RobertImage);
imshow("RobertImage", RobertImage);
下面是自定义并实现一个Roberts 算子:
从效果上看我拟合的没有opencv集成的好,但是原理是一样的。
代码:
Mat Robertsoperation(Mat &src,int type);
Mat Robertsoperation(Mat& src, int type)
{
//type =1,2,3 分别表示 135 35 和合并后的结果
Mat dstImage = src.clone();
int nrows = src.rows;
int ncols = src.cols;
for (int i = 0; i < nrows-1; i++)
{
for (int j = 0; j < ncols - 1; j++)
{
// 135度
int t1 = ((src.at(i, j) - (src.at(i + 1, j + 1)))* (src.at(i, j) - (src.at(i + 1, j + 1))));
// 45 度
int t2 = ((src.at(i+1, j) - (src.at(i , j + 1 ))) * (src.at(i + 1, j) - (src.at(i, j + 1))));
if ( type == 1 )
{
dstImage.at(i, j) = (uchar)t1;
}
else if (type == 2)
{
dstImage.at(i, j) = (uchar)t2;
}
else
{
dstImage.at(i, j) = (uchar)sqrt(t1+t2);
}
}
}
return dstImage;
} 3、 Sobel
具体步骤:
a:分解矩阵,将矩阵分解成一个二项式系数*差分算子的过程
b: 先求出二项式系数,然后再用这个系数计算差分算子
c:卷积运算 :
算子解释:
Sobel(inputArray,outputArray,int ddepth,int dx,int dy,int ksize=3,double scale=1,double delta=0,int borderType=BORDER_DEFAULT)
*第一个参数,输入图像。
*第二个参数,输出图像。
*第三个参数,输出图像深度。
*第四个参数,x方向上的差分阶数。
*第五个参数,y方向上的差分阶数。
*第六个参数,Sobel核的大小,必须是奇数。
*第七个参数,计算导数值时可选的缩放因子,默认值1,表示默认情况下没用应用缩放。
*第八个参数,表示在结果存入输出图像之前可选的delta值 (这个参数默认是0.0)
*第九个参数,扩充边界模式。效果如下:
代码显示:
int factorial(int n)
{
int fact = 1;
if (n==0)
{
return fact = 1;
}
for (int i = 1; i < n; i++)
{
fact *= i;
}
return fact;
}
Mat CreateDiff(int n);
void my_sobel(Mat& src, Mat dst, int x_flag, int y_flag, int winsize, int borderType);
// 得到一个平滑算子 n为 窗口的大小
Mat Getsmooth(int n)
{
Mat smooth = Mat::zeros(Size(n,1),CV_32FC1);
for (int i = 0; i < n; i++)
{
smooth.at(0, i) = factorial(n - 1) / (factorial(i) * (factorial(n - i - 1)));
}
//当窗口 3 二项式展开的系数是 1 2 1 差分算子是 1 0 -1
//当窗口 5 二项式展开的系数是 1 4 6 4 1 差分算子是 1 2 0 -2 -1
return smooth;
}
//从上面的的二项式系数中 得到 差分算子
Mat CreateDiff(int n)
{
Mat Diff = Mat::zeros(Size(n, 1), CV_32FC1);
Mat Diff_pres = Getsmooth(n-1);// n=5 是返回的是1 3 3 1
for (int i = 0; i < n; i++)
{
if (i == 0)
{
Diff.at (0, i) = 1;
}
else if (i == n - 1)
{
Diff.at (0, i) = -1;
}
else
{
Diff.at (0, i) = Diff_pres.at(0, i) - Diff_pres.at(0, i - 1);
}
}
//当n=3 时候,Diff_pres= 1, 1 Diff_pres.at(0, i)=1, Diff_pres.at(0, i - 1)=1
// Diff =1 0 -1
//当n=5 时候,Diff_pres= 1 3,3 1
// Diff =1 2 0 -2 -1
return Diff;
}
// 是用sobel 算子,对图像完成卷积 ,当 x-flag=0,-->x的
void my_sobel(Mat& src, Mat dst, int x_flag, int y_flag, int winsize, int borderType)
{
// winsize 应该是》=3的奇数
CV_Assert(winsize>=3&& winsize%2==1);
// 得到 二项式的系数
Mat smooth = Getsmooth(winsize);
// 得到差分系数
Mat smoothdiff = CreateDiff(winsize);
//当x_flag!=0 是, 返回图像与水平方向上的卷积
if (x_flag != 0)
{
// smooth.t() 表示矩阵的转置
sepFilter2D(src, dst, CV_32FC1, smooth.t(), smoothdiff, Point(-1,-1), borderType);
}
// 当x_flag==0 && y_flag!=0 的时候 垂直方向的
if (x_flag == 0 && y_flag != 0)
{
sepFilter2D(src, dst, CV_32FC1, smooth, smoothdiff.t(), Point(-1, -1), borderType);
}
}
int main(int args, char* arg)
{
Mat src, src_gray, dest1, dest2, dest3, dest4, dest5, dest6;
// point
src = imread("C:\\Users\\19473\\Desktop\\opencv_images\\305.jpg");
if (!src.data)
{
printf("could not load image....\n");
}
cvtColor(src, src_gray, COLOR_BGR2GRAY);
imshow("原图", src_gray);
// sobel X方向上的算子
Mat sobel_kernel_x = (Mat_(3, 3) << 1, 0, -1, 2, 0, -2, 1, 0, -1);
filter2D(src_gray, dest3, -1, sobel_kernel_x, Point(-1, -1), 0.0);
imshow("Opencv sobel_X", dest3);
// sobel Y 方向上的算子
Mat sobel_kernel_y = (Mat_(3, 3) << 1, 2, 1 , 0, 0, 0, -1, -2, -1);
filter2D(src_gray, dest4, -1, sobel_kernel_y, Point(-1, -1), 0.0);
imshow("Opencv sobel_Y", dest4);
//================================================================
// 自定义sobel算法
my_sobel(src_gray, dest3, 1, 0, 3, BORDER_DEFAULT);
imshow("自定义-水平方向", dest3);
my_sobel(src_gray, dest3, 0, 1, 3, BORDER_DEFAULT);
imshow("自定义-垂直方向", dest4);
waitKey(0);
return -1;
} 4、 Prewitt 边缘检测
代码如下:
// 分离卷积运算
void conv2d(InputArray src, InputArray kernel, OutputArray dst, int ddepth,
Point achor = Point(-1, -1),
int borderType = BORDER_DEFAULT)
{
// 卷积运算的第一步,将卷积核逆时针旋转180度 。。 主要是为了计算方便
Mat kernelFlip;
flip(kernel, kernelFlip,-1);
// 第二步才开始计算
filter2D(src,dst, ddepth, kernelFlip, achor,0.0, borderType);
//InputArray src, OutputArray dst, int ddepth,
// InputArray kernel, Point anchor = Point(-1, -1),
// double delta = 0, int borderType = BORDER_DEFAULT
}
// 卷积的顺序不一样
void Mysepfilter2D_YX_order( InputArray src, OutputArray src_xy, int ddepth, InputArray kernel_y,
InputArray kernel_x, Point achor = Point(-1, -1), int border_type = BORDER_DEFAULT)
{
Mat tempk;
conv2d(src, kernel_y, tempk, ddepth, achor, border_type);
conv2d(tempk, kernel_x, src_xy, ddepth, achor, border_type);
}
void Mysepfilter2D_XY_order(InputArray src, OutputArray src_xy, int ddepth, InputArray kernel_x,
InputArray kernel_y, Point achor = Point(-1, -1), int border_type = BORDER_DEFAULT)
{
Mat tempk;
conv2d(src, kernel_x, tempk, ddepth, achor, border_type); // 垂直
conv2d(tempk, kernel_y, src_xy, ddepth, achor, border_type);// 水平
}
void myPrewitt( InputArray src, OutputArray dst, int ddepth, int x, int y, Point achor = Point(-1, -1), int border_type = BORDER_DEFAULT)
{
Mat prewitt_xy = (Mat_(3, 1) << 1, 1, 1);
Mat prewitt_xx = (Mat_(1, 3) << 1, 1, 1);
Mat prewitt_yx = (Mat_(3, 1) << 1, 1, 1);
Mat prewitt_yy = (Mat_(1, 3) << 1, 1, 1);
if (x!=0&&y==0)
{
Mysepfilter2D_YX_order(src,dst, ddepth, prewitt_xy, prewitt_xx);
}
if (y != 0 && x == 0)
{
Mysepfilter2D_YX_order(src, dst, ddepth, prewitt_yx, prewitt_yy);
}
}
int main(int args, char* arg)
{
Mat src, src_gray, dest1, dest2, dest3, dest4, dest5, dest6;
// point
src = imread("C:\\Users\\19473\\Desktop\\opencv_images\\305.jpg");
if (!src.data)
{
printf("could not load image....\n");
}
cvtColor(src, src_gray, COLOR_BGR2GRAY);
imshow("原图", src_gray);
// prewitt 卷积
Mat p_x;
myPrewitt(src_gray, p_x,CV_32FC1,1,0);
Mat p_y;
myPrewitt(src_gray, p_y, CV_32FC1, 0, 1);
// 水平方向和垂直方向的 边缘强度
// 数据类型转换。边缘强度的灰度显示
Mat abs_image_prewitt_x, abs_image_prewitt_y;
convertScaleAbs(p_x, abs_image_prewitt_x,1,0);
convertScaleAbs(p_y, abs_image_prewitt_y,1,0);
imshow("垂直方向边缘",abs_image_prewitt_x);
imshow("水平方向边缘", abs_image_prewitt_y);
// 通过上面求得的两个方向上的边缘求得最终的边缘强度
//Mat abs_image_prewitt_x2, abs_image_prewitt_y2;
//pow(abs_image_prewitt_x, 2.0, abs_image_prewitt_x2);
//pow(abs_image_prewitt_y, 2.0, abs_image_prewitt_y2);
//Mat edge=Mat::zeros(src.size(),CV_32F);
//sqrt((abs_image_prewitt_x2 + abs_image_prewitt_y2), edge);
edge.convertTo(edge,CV_8UC1);
imshow("边缘强度", edge);
waitKey(0);
return -1;
} 5、 Canny(最常用的算子)
基于卷积运算的边缘检测算法,比如sobel prewitt算子有几个缺点:
a、没有充分的利用梯度的方向
b、最后输出的边缘二值图只是简单的利用了阈值进行处理,当阈值很大的时候就会损失很多的边缘,反之亦然
那么canny 是这这个基础上进行了一部分的优化:(1) 基于边缘梯度方向的非极大值抑制。
(2) 双阈值的滞后阈值处理。
Canny 边缘检测的近似算法的步骤如下
第一步:图像矩阵I 分别与水平方向上的卷积核和垂直方向上的卷积核卷积得到dx和dy ,然后利用平方和的开方magnitude=sqrt(dx^2+dy^2)得到边缘强度。举例如下:

sobel 在边缘检测的过程中将值大于255的截断为255然后得到一个二值图像。
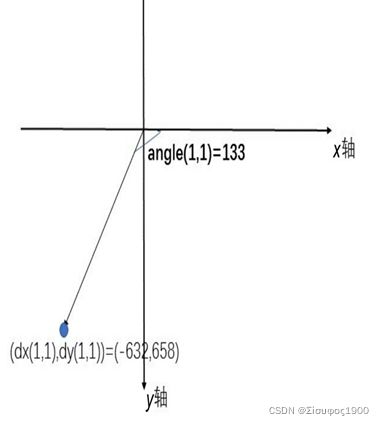
第二步:利用第一步计算出的dx和dy ,计算出梯度方向angle=arctan 2(dy ,dx), 即对每一个位置(r,c),angle(r,c)=arctan 2(dy (r,c),dx(r,c))代表该 位置的梯度方向,一般用角度表示,即angle(r,c)∈[0,180]∪[-180,0]。得到一个关于角度的矩阵angle:
以上图133中心点为例
水平方向:dx=(154-133)
垂直方向:dx=(175-133)
第三步:对每一个位置进行非极大值抑制的处理 ,magnitude是从第一步里面得到的及边缘矩阵,在这里要进行一个非极大值抑制的处理,所以在边缘扩充的时候用的是补零的方式。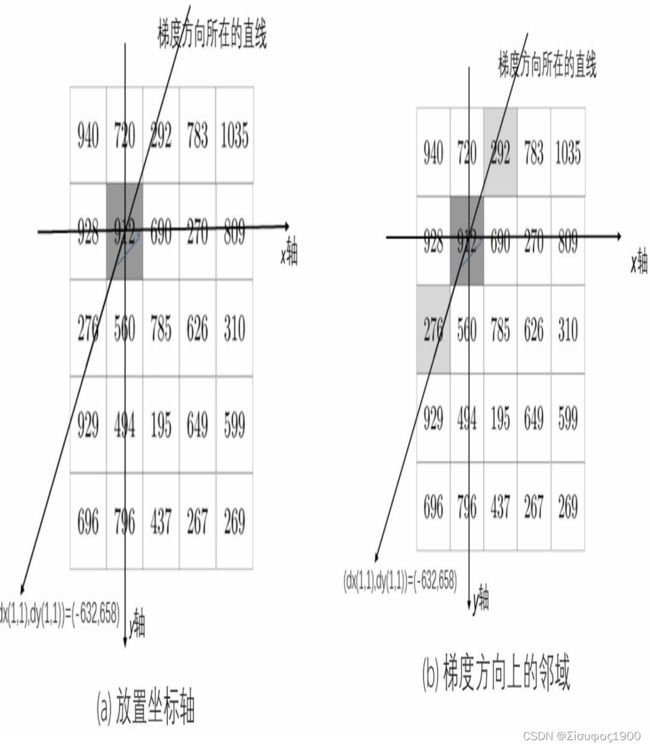

上图右边的图像中,左边为nonMaxSup(1,1)的值为912,那么现在需要做的是严重这条梯度方向的线走,经过邻域区域(我们目前默认是3x3的邻域)的值和(1,1)的值(912)做对比,若nonMaxSup(1,1)>是由于的这条线上邻域的值,那么(1,1)就是极大值,则nonMaxSup(1,1)=magnitude(1,1)=912,若nonMaxSup(1,1)不全大于是由于的这条线上邻域的值,则nonMaxSup(1,1)=0。用同样的方法计算nonMaxSup(1,2)的值得到nonMaxSup(1,2)=0。
总结上述非极大值抑制的过程:如果magnitude(r,c)在沿着梯度方向angle(r, c)上的邻域内是最大的则为极大值;否则,设置为0。
非极大值抑制的实现:
非极大值抑制的第二种方式:用插值法拟 合梯度方向上的边缘强度,这样会更加准确地衡量梯度方向上的边缘强度
插值方式:L1::L2=M:(1-M),那么可以近似的算出左上角的插值 P1= M*292+(1-M)*720,同理可以算出右下角:P1= M*276+(1-M)*560,然后比较P1 和P2再和920比较大小,若920>P1&&920>P2,则为极大值,否则不是极大值。一般将梯度方向离散化为以下四种情况:
· angle(r,c)∈(45,90]∪(-135,-90] · angle(r,c)∈(90,135]∪(-90,-45] · angle(r,c)∈[0,45]∪[-180,-135] · angle(r,c)∈(135,180]∪(-45,0)
第四步:双阈值的滞后阈值处理。经过上一步的极大值抑制处理之后,一般需要阈值化处理(threshold 和 adaptiveThreshold),常用阈值滞后方法:高阈值 低阈值,具体方法如下:(1) 边缘强度大于高阈值的那些点作为确定边缘点。
(2) 边缘强度比低阈值小的那些点立即被剔除。
(3) 边缘强度在低阈值和高阈值之间的那些点,可以理解为,首先选定边缘强度大于高阈 值的所有确定边缘点,然后在边缘强度大于低阈值的情况下尽可能延长边缘(该像素仅仅在连接到一个高于高阈值的像素时被保留)。
上述所说的高阈值一般是低阈值的2~3倍。
Canny算子边缘检测流程
算子解释:
void Canny(inputArray,outputArray,double threshold1,double threshold2,int apertureSize=3,bool L2gradient=false)
*第一个参数,输入图像,且需为单通道8位图像。
*第二个参数,输出的边缘图。
*第三个参数,第一个滞后性阈值。用于边缘连接。
*第四个参数,第二个滞后性阈值。用于控制强边缘的初始段,高低阈值比在2:1到3:1之间。
*第五个参数,表明应用sobel算子的孔径大小,默认值为3。
*第六个参数,bool类型L2gradient,一个计算图像梯度幅值的标识,默认值false。显示: