【数据分析师---数据分析基础】第一章:Numpy功能介绍及应用
Numpy使用梳理
- 1 Numpy介绍
-
- 1.1 科学计算
- 1.2 Numpy历史和发展
- 1.3 Numpy的安装
- 2 Numpy和Python List的对比
-
- 2.1 相同之处
- 2.2 不同之处
- 2.3 操作实践
- 3 array()数组
-
- 3.1 array()数组的生成及列表转换
- 3.2 多维数组的创建
- 4 arange()方法
- 5 zeros/ones/empty/eye方法
-
- 5.1 np.zeros()
- 5.2 np.ones()
- 5.3 np.empty()
- 5.4 np.eye()
- 6 linespace/random方法
-
- 6.1 np.linespace()
- 6.2 np.random()
-
- 6.2.1 random.randn()产生正态分布数值
- 6.2.2 random.normal() 标准正态分布
- 6.2.3 random.rand()均匀分布
- ★★★6.2.4 random.randint() 生成随机整数
- 7 shape/index方法
-
- 7.1 shape()
- 7.2 index()
- 8 Numpy数字运算与广播
-
- 8.1 Numpy数字运算
- 8.2 Numpy的广播功能
-
- 8.2.1 标量计算
- 8.2.2 广播功能解释
- 8.2.3 神奇的1
- 9 reshape/resize方法
-
- 9.1 reshape()改变数组尺寸
- 9.2 resize()改变数组大小
- 10 numpy的形状变化功能
-
- 10.1 flatten()/ravel()方法
- 10.2 transpose()/swapaxes()方法
- 11 numpy的数据合并与拆分
-
- 11.1 concat/stack/split方法
- 11.2 append/insert/delete方法
- 12 Numpy的matrix介绍
-
- 12.1 矩阵加法和乘法
- 12.2 逆矩阵和矩阵幂
- 12.3 矩阵方程和行列式求解
- 13 Numpy中条件逻辑表述为数组运算
手动反爬虫: 原博地址
知识梳理不易,请尊重劳动成果,文章仅发布在CSDN网站上,在其他网站看到该博文均属于未经作者授权的恶意爬取信息
如若转载,请标明出处,谢谢!
1 Numpy介绍
1.1 科学计算
科学计算主要是利用计算机的算力进行数据的计算和方程求解,具体包括如下内容:
- 一个强大的N维数组对象 ndarray
- 广播功能函数
- 整合 C/C++/Fortran 代码的工具
- 线性代数、傅里叶变换、随机数生成,微积分求解等功能
1.2 Numpy历史和发展
- Numpy(Numerical Python) 是 Python 语言的一个扩展程序库,支持大量的维度数组与矩阵运算。
- Numpy 的前身 Numeric 最早是由 Jim Hugunin 与其它协作者共同开发
- 2005 年,Travis Oliphant 在 Numeric 中结合了另一个同性质的程序库 Numarray 的特色,并加入了其它扩展而开发了 NumPy。
- NumPy 为开放源代码并且由许多协作者共同维护开发。
1.3 Numpy的安装
- NumPy 通常与 SciPy(Scientific Python)和 Matplotlib(绘图库)一起使用。
- 这种组合广泛用于替代 Matlab,是一个强大的科学计算环境,有助于我们通过 Python 学习数据科学或者机器学习。
- 利用Python的PIP包管理器可以方便的安装Numpy套件,当然也可以利用Anaconda的套件环境快速安装Numpy环境(默认Anaconda是自动包含的)。
2 Numpy和Python List的对比
2.1 相同之处
(1)作为容器都是可以存储数据 Storing Data
列表数据:ls = [1,2,3,4] numpy数组: ar = np.array([1,2,3,4])
(2)容器内数据可更新 Mutable
列表的添加功能:ls.append()/ls.extend() numpy数组添加: ar.append()
(3)可索引搜索 Can be indexed
列表的索引:ls[0] numpy数组的索引:ar[0]
(4)可分片 Slicing Operation
列表的切片:ls[0:2] numpy数组的索引:ar[1:3]
2.2 不同之处
(1)List 可以存储不同的数据类型对象
ls = [1,'1',2.34]
(2)Numpy Array存储的都是同类型数据对象
ar = np.array([1,2,3,4]) 都是数值类型对象
★★★(3)Operation 快速操作
np.array([1,2,3,4]) + np.array([2,3,4,5]) = np.array([3 5 7 9])
(4)List是内置结构,Numpy需要特别安装
list是python的关键字,对应列表数据类型,可以直接拿来用,但是numpy是科学计算的第三方包,需要单独下载安装(Anaconda中自带的有)
★★★(5)NumpyArray是C语言写的。可以比List操作快10-100倍。适合大数据分析
2.3 操作实践
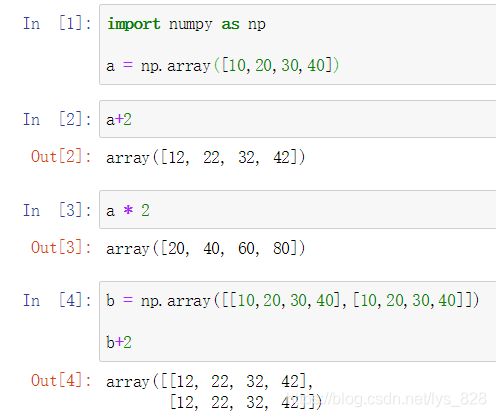
(1)创建数组并进行计算,代码如下,可以发现操作都是针对于整个数组

(2)创建列表进行计算,代码如下,可以发现无法直接进行全部数据的运算,需要借助for循环
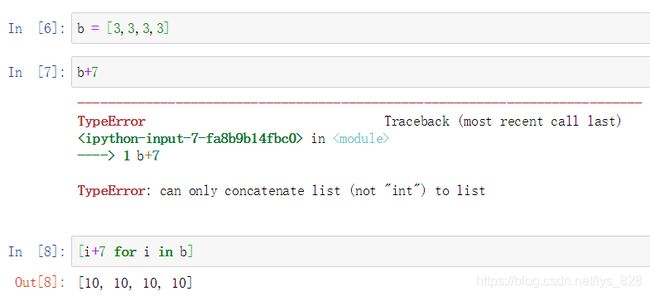
(3)numpy与list计算性能对比
为了比较两者计算的性能,引入time对两者的操作进行计时,首先是使用纯python的list数据进行计算数据量为10000000时候加法操作,代码如下
import numpy as np
import time
size_of_vec = 10000000
def pure_python():
start = time.time()
x = range(size_of_vec)
y = range(size_of_vec)
z = []
for i in range(len(x)):
z.append(x[i] + y[i])
return time.time() - start
print(pure_python())
输出结果为:4.622632265090942
然后使用numpy的来计算这10000000的数据量,封装函数和执行代码如下
def numpy_version():
start = time.time()
x = np.arange(size_of_vec)
y = np.arange(size_of_vec)
z = x + y
return time.time() - start
print(numpy_version())
输出结果为:0.058849334716796875
假使10000000的数据量继续往上调大5倍执行,最后看一下两种方式的计算性能的比值,结果如下

3 array()数组
使用np.array()方法可以从一个列表或者元祖创建一个Numpy数组,可以任意指定数据的维度,如下,由于人类可以理解的维度只有三维,只能列举三种,其实数据是可以有多维的

3.1 array()数组的生成及列表转换
通过array()方法生成的数组,最后查看数据类型是属于Ndarray,其中填入到array()括号中的数据可以是元组也可以是列表类型

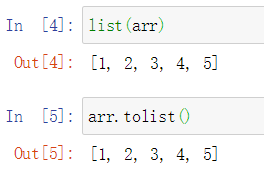
如果要将Ndarray数据转换成为list列表对象,可以直接加上list或者使用数组的tolist()方法,代码如下
3.2 多维数组的创建
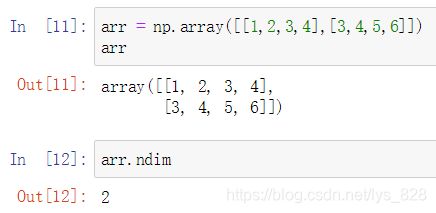
查看数据是几维的,可以数括号内第一个元素前面有几个左括号,或者直接使用ndim()方法查看
(1)0D scalars 标量

(2)1D array

(3)2D array
(4)3D array

其它高维数据的创建也是类似,就不再展示了,还有一种比较方便的操作,直接使用ndmin参数指定,比如

除了指定数据的维度,还可以通过dtype参数指定创建数组中数据的类型,比如都是浮点数

4 arange()方法
使用arange()方法可以基于数值范围的数组创建数组,它创建具有均匀间隔的值的ndarray实例,并返回对其的引用
语法结构:
numpy.arange([start, ]stop, [step, ], dtype=None) -> numpy.ndarray
操作演示:绿色为起始包含,红色为终止不包含
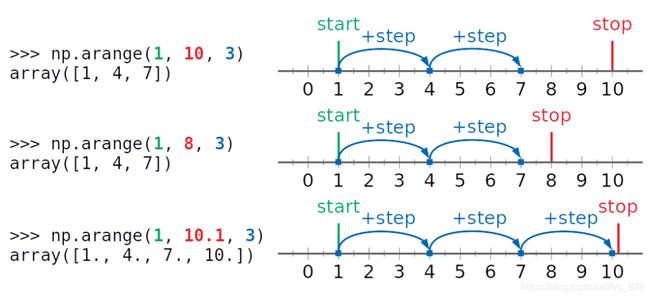
对于反方向的进行数据生成,可能会和numpy的版本不同而导致生成的数据顺序不同,比如目前使用的1.19.1版本,到底是正序还是逆序跟自己安装的numpy的版本实际输出为准,这一点不用太过纠结
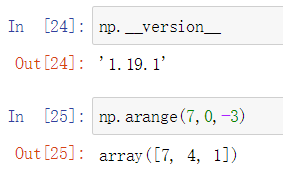
代码操作如下,根据前面的语法结构对应下面的输出,可以发现可以只填写起始和终止的位置,但是步长默认会是1,如果不指定起始位置,就默认是0,但是如果只给定了stop参数并对应了数值,运行结果就会报错,因为找不到起始量
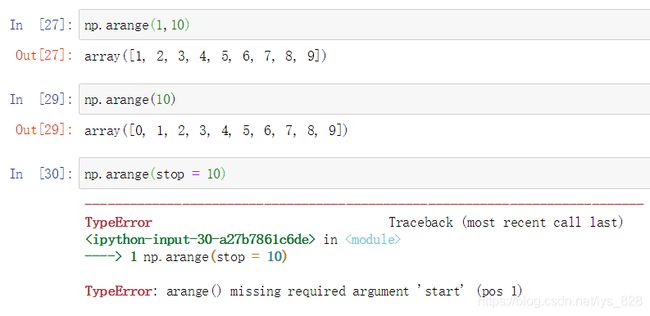
起始值也可以是负值,代码如下

在最开始介绍了数组和列表都是有索引和切片的功能,那么这里还可以根据步长取值进行索引及切片

计算操作,arange()方法生成的数组是可以直接进行计算

Numpy的arange()与Python自带的range性能对比,测试代码如下,发现两者相差了100倍,特别是等待了很久把第一行代码运算完毕,第二行瞬间就完成了

5 zeros/ones/empty/eye方法
5.1 np.zeros()
用于产生全0数组,语法结构:numpy.zeros(shape, dtype = None, order = ‘C’) ,Return a new array of given shape and type, with zeros.
使用一个方法的时候,如果需要知道设计文档说明,可以直接使用help(方法名)进行访问,比如这里就可以使用help(np.zeros),然后按照设计文档中的例子进行测试输出,代码如下,注意对应numpy数组来说,传递元祖和列表最后生成的结果是一样的

5.2 np.ones()
用于产生全1数组,语法结构:numpy.ones(shape, dtype = None, order = ‘C’) ,Return a new array of given shape and type, with ones.
该方法使用与上面的np.zeros()类似,itemsize代表着字节大小

5.3 np.empty()
用于产生空数组,语法结构:numpy.empty(shape, dtype = float, order = ‘C’), Return a new array of given shape and type, with random values. 这里的随机不是真正的随机,而是有电脑记忆的一些数值
比如将上面np.ones()的操作改成np.empty(),对应的输出如下,注意random values的含义

5.4 np.eye()
用于产生N*N对角线数组,语法结构:numpy.eye(R, C = None, k = 0, dtype = type <‘float’>) ,–The eye tool returns a 2-D array with 1’s as the diagonal and 0’s elsewhere. The diagonal can be main, upper, or lower depending on the optional parameter k.
其中参数k代表着对角线偏移的程度,大于0是上移,小于0时下移。一般为方阵,也可以指定非方阵

6 linespace/random方法
6.1 np.linespace()
用于产生x1,x2之间的N点行线性的矢量,其中x1、x2、N分别为起始值、终止值、元素个数。若默认N,默认点数为50,语法结构:numpy.linspace(start, stop, num = 50, endpoint = True, retstep = False, dtype = None) ,Returns number spaces evenly w.r.t interval. Similar to arange but instead of step it uses sample number.
★★★ 还可用于绘图时x,y轴刻度的设置,或者x,y值的指定
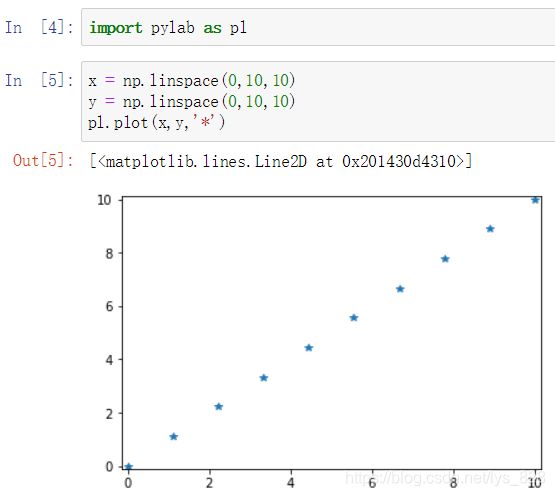
6.2 np.random()
用于产生随机数据数组。
6.2.1 random.randn()产生正态分布数值
语法结构:numpy.random.randn(d0, d1, …, dn) ,creates an array of specified shape and fills it with random values as per standard normal distribution.使用random.randn()方法可以随机生成正态分布的数值,能够自己指定数据的维度,也能进行同维度数据的计算

6.2.2 random.normal() 标准正态分布
语法结构:random.normal(loc=0.0, scale=1.0, size=None),Draw random samples from a normal (Gaussian) distribution 随机生成期望值为0,标准差为1的数据,所以只需要指定一个size参数即可,生成指定维度的数据,比如三行四列

6.2.3 random.rand()均匀分布
语法结构: random.rand(d0, d1, ..., dn), Random values in a given shape.随机生成一个[0,1)之间的浮点数或N维浮点数组,注意这里和生成正态分布的随机数一样,指定维度的时候,直接给数值就可以了,不需要加括号

★★★6.2.4 random.randint() 生成随机整数
语法结构:randint(low, high=None, size=None, dtype=int), Return random integers from low (inclusive) to high (exclusive).若high不为None时,取[low,high)之间随机整数,否则取值[0,low)之间随机整数,且high必须大于low,dtype参数:只能是int类型。该方法在日常处理数据中还是很常用的。

7 shape/index方法
7.1 shape()
用于查看矩阵的大小形状,数组的形状可以定义为每个维度中元素的数量。
如果按照之前array()指定ndmin参数,查看一下对应的维数和尺寸,如下

7.2 index()
NumPy是用于在均匀n维数组上进行计算的软件包。在numpy中,尺寸称为轴。和列表中的索引类似,矩阵中的索引一样从0开始计数,最大尺寸为总数-1,反向索引从-1开始,这一点和Python列表也很相似,Slicing切片功能也和列表相似,只是扩展到更高维度。
通过下面两个列表相乘的例子,可以发现对于列表直接相乘,系统无法找到对应的索引也就无法进行相乘,只能通过遍历循环,而numpy数组可以直接自动匹配索引进行相同位置元素的乘法,最后得到目标结果
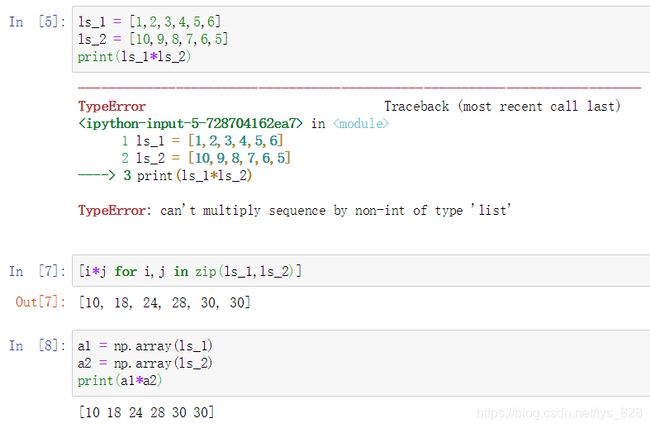
接下来进行直接索引取值,如果是取单个值,直接就在列表中填入相应的位置数值(注意索引是从0开始的),如果是多个索引,直接给出一个列表,最后的结果会按照列表的数值顺序输出(这里数值顺序就是对应索引位置)

★★★★★高维数据的索引
注意纵横轴都是从0开始的,如果是反向索引就是从-1开始,结合下面的图片进行理解

代码验证一下,使用了reshape()方法,后面就会介绍到,最最最核心的是要理解一个问题:多维索引中第一个参数对应行,第二个参数对应于列

可以进一步的参考这个图示
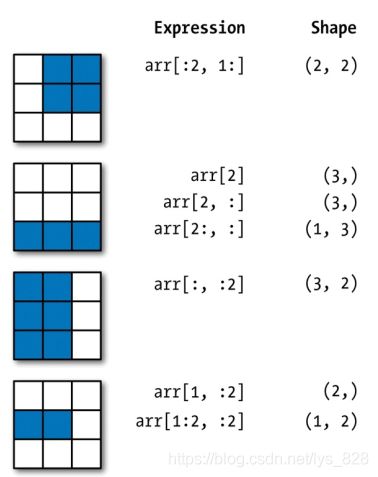
★★★★布尔索引,可以通过条件判断的方式对满足的数据进行提取,但是需要注意,这种操作会破坏原有的结构

8 Numpy数字运算与广播
8.1 Numpy数字运算
- Numpy包含大量的各种数学运算。其中提供了标准的三角函数,算数运算功能,和处理复数等
- 具备标量计算功能,常规的代数运算都可以实现
- 具有矩阵运算特性,支持同尺寸矩阵的各种数学运算
8.2 Numpy的广播功能
- 广播(Broadcast)是指Numpy在算数运算期间如何处理具有不同维数的数组,这会导致某些约束,较小的数组将在较大的数组上广播,以使它们具有兼容的形状
- 广播提供了一种对数组操作进行矢量化的方法,从而使循环在C中发生,而不是在python中发生,因为numpy是在c中实现的,所以这样做就不需复制不必要的数据,从而实现高效的算法实现
- 在某种情况下,广播并不是一个好方式,因为广播会导致内存使用效率低下,从而减慢计算速度
- 如果数组的尺寸不同,则将低尺寸数组的形状扩充,直到两个形状的长度相同
- 如果两个数组的尺寸相同,或者其中一个数组的尺寸为1,则两个数组在尺寸上兼容
- 如果阵列与所有尺寸兼容,则可以一起广播
- 广播之后,每个数组的行为就好像它们的形状等于两个输入数组的元素方向的最大值一样
- ★★★★★★在一个数组的大小为1,而另一个数组是大于1的任何维度中,第一个数组的行为就像是沿着该维度复制一样
8.2.1 标量计算
8.2.2 广播功能解释
从上面的输出结果分析,其中a的尺寸为(1,5),直接加上数值2,该数值的尺寸是(1,1),按照上面介绍numpy的广播功能的最后一个核心要点的时候,该数值就会自动进行广播,从而转化为同尺寸的数组,进而实现加法操作,过程就如下图
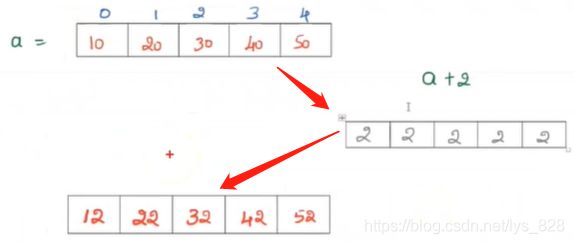
再进一步解释,如下的数组。其中a的尺寸为(3,2),b尺寸为(3,)也就是(1,3),c的尺寸为(2,)也就是(1,2)。

首先看一下a+c,其中列方向上都一致,然后在行方向上c是1,因此可以进行广播,转化为和a一样尺寸的大小,故a+c可以计算。
再看一下a+b,两者列方向上不一致,行方向上b是1,那么对b进行广播,也化成3行,可以发现最终c的尺寸是(3,3),但是a的尺寸只有(3,2),所以最后a+b运算报错
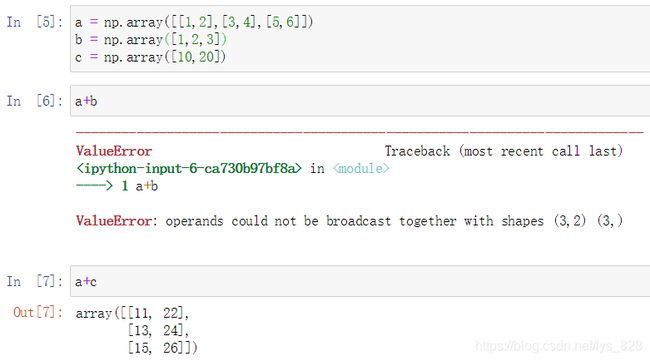
8.2.3 神奇的1
比如下图两个数组进行相加,结果如何呢?,其中a的尺寸为(3,1),b的尺寸为(1,3)

首先看一下列方向上,a是1,那么就进行扩展就可以化为3,这样列方向上就相同了
再看行方向上,b是1,那么就可以进行扩展为a对应的长度也为3,这样最终两个数组扩展为了(3,3),满足相加的条件
代码验证一下,最后的结果仍然是(3,3),然后就是对应位置的元素相加,结果与下图一致

9 reshape/resize方法
9.1 reshape()改变数组尺寸
之前介绍了shape()方法,可以直接返回数组的尺寸,即是数据有多少行和多少列,而reshape()方法就是在不改变数据内容的情况下,改变一个数组的格式,前面也用过一次。
- order参数:可选范围{‘C’,‘F’,‘A’}。使用索引顺序读取元素,并按照索引顺序将元素放在变换后的数组中。如果不进行order参数的设置,默认就是C
- “C”指的是用C类写的读索引顺序的元素,最后一个维度变化最快,第一个维度变化最慢。以二维数组为例,简单来讲就是横着读,横着写,优先读/写一行
- "F"指的是用FORTRAN类索引顺序读/写元素,最后一个维度变化最慢,第一个维度变化最快。竖着写,竖着读,优先读/写一列。
- 注意:"C"和"F"选项不考虑底层数组的内存布局,只引用索引的顺序
- “A”指的是所生成的数组的效果与原数组a的数据存储方式有关,如果数据是按照FORTRAN存储的话,它的生成效果与”F“相同,否则与“C”相同。这里可能听起来有点模糊,下面会给出示例。
代码操作,可以手动指定reshape的两个形状参数,也可以在指定行之后,使用-1让系统自动匹配对应的列数
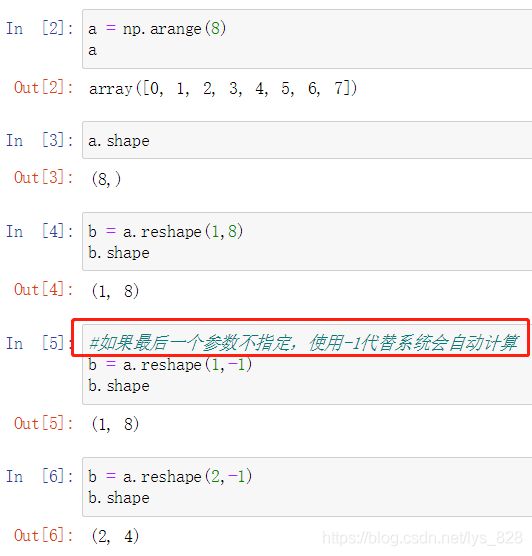
但是如果数组的尺寸乘积无法整除行数就会报错
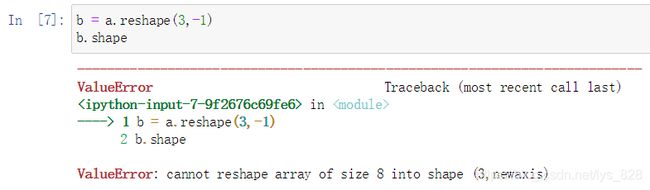
对于order参数的理解,如果不进行格式转化,最后使用A参数就会和C参数一致,为了显示出A的效果,首先要进行FORTRAN存储数组的转换,在进行不同参数下的reshape,如下,一般默认是参数C就可以了

9.2 resize()改变数组大小
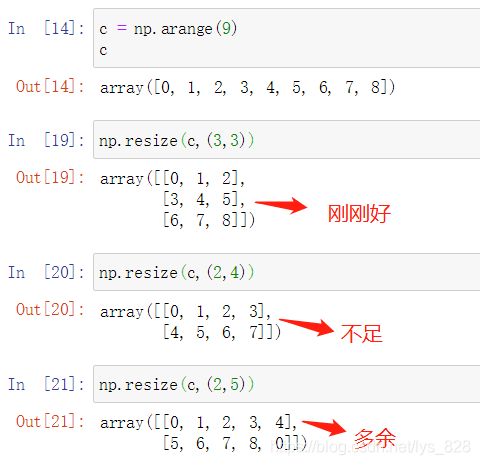
- 有返回值的resize,不会改变原来的array的shape
- 若resize后需要的数据量变少,会丢弃一些数据
- 若resize后需要的数据量变多,会补0
注意这里使用的是np.resize()方法进行变换的而不是变量.resize()方法,这两个是有区别的,为避免不报错的情况下尽量使用第一种方式
10 numpy的形状变化功能
10.1 flatten()/ravel()方法
- flatten() 返回的是一个折叠成一维的数组,该函数只适用于numpy对象,即array和matrix
- ravel()和 flatten() 一样,两者的功能是一致的,将多维数组降为一维
- 区别是:返回的是拷贝还是返回视图,flatten() 返回的是一份拷贝对象,对该对象所做的修改不会影响原始矩阵,而ravel()返回的是视图,修改时会影响原始矩阵
首先是直接进行数据的降维操作,两种方式处理后的结果是一致的

然后对比一下两者的变化,主要是对变量的修改是否改变原有的数组

10.2 transpose()/swapaxes()方法
- transpose()按照多维数组的轴的索引进行变换,简单而言就是行和列进行对换
- swapaxes()轴变换功能,是上述transpose()的另一种等价形式
- swapaxes()只接受两个参数,即表示需要转换的两个轴的索引,所以在三维以上的情况下,transpose()会好一些
其中.transpose()方法就等同于.T的操作,还有swapaxes()方法对于对于pandas的多层次索引会有这很棒的应用,直接转换一级索引和二级索引,之后的pandas中介绍

11 numpy的数据合并与拆分
11.1 concat/stack/split方法
- concat在已有的维度上进行拼接,能够一次完成多个数组的拼接,默认axis=0
- stack在新的维度上进行拼接
- split是把一个数组从左到右按照顺序切分
对于concat连接数据,可以根据指定的axis进行不同方向的拼接,concat是concatente的简称,pandas里面直接使用的concat,也是有相同的操作,之后会讲

如果axis=None,就相当是将数组给拍扁了,输出如下

对于stack()方法的使用,可以分为垂直拼接和水平拼接,注意行列数的限制,尽量保持一致

对于split()方法的使用,也是分水平和垂直的两种,代码操作如下

11.2 append/insert/delete方法
- append(arr,values,axis=None)中,axis是可选参数。如果不设置axis,则apeend()返回的结果是将arr和values展平后进行拼接
- insert(arr,obj,values,axis)和append()类似,但是这个方法更灵活,append()的新增数据只能在每行每列的最后,其位置是固定的,insert()是可以按照obj进行指定的,insert()中的axis的作用与append()中的作用相同,但其在进行插入的时候,对arr和values的维度不再有限制,默认axis = None
- delete(arr,obj,asix)函数实现按照axis和obj,对arr进行元素删除的功能,如果没有设置axis,则对arr进行flatten之后再删除
首先看一下insert()方法的使用,注意默认axis = None,使用时应该留心这里

指定axis参数后,就是如下输出了,对于每行或者每列都会添加相同的值
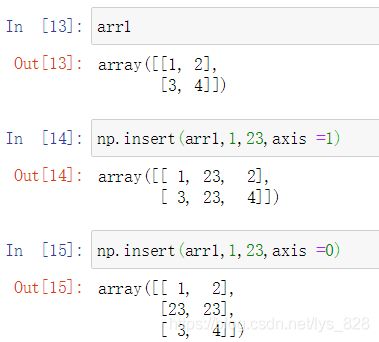
对于append()方法的使用,一个是默认还末尾结束的时候插入,还有一个就是插入的数据的维数还要和原数据维数一致(数据的格式要严格)

delete()方法较为简单,操作如下,还是和之前的规则一样

12 Numpy的matrix介绍
- Numpy中存在两种不同的数据类型(矩阵matrix和数组array),都可以用于处理行列表示的数字元素。虽然它们看起来很相似,但是在这两个数据类型上执行相同的数学运算可能得到不同的结果,其中Numpy函数库中的matrix与Matlab中的matrices等价
- Numpy模块中的矩阵对象np.matrix,包含了矩阵数据的处理,矩阵计算,以及基本的统计功能,转置,可逆性等等,包括对复数的处理,均在matrix对象中
- matrix是array的分支,两者在很多时候是通用,但官方建议如果两个可以通用就选择array,因为array更灵活,速度也更快,很多人也把二维的array翻译成为矩阵
12.1 矩阵加法和乘法
对比矩阵的加法是没有问题的,但是如果进行矩阵的运算,显然第一种方式出现了错误,并不是真正的运算结果,而第二种方式才是真实的

由于说了array的功能比较强大,当然有算矩阵乘法的方法dot(),代码如下

12.2 逆矩阵和矩阵幂
之前复习的线性代数就派上用场了,关于逆矩阵和矩阵幂的概念。
如果求解逆矩阵,直接使用np.linalg.inv(a)方法,最后验证a*b就是单位阵,由于python精度的问题,会出现数值浮动,但不是影响结果

对于矩阵幂的求解使用np.linalg.matrix_power(a,5)即可

有特殊的情况,比如0次幂和-1次幂,看看结果如何?输出发现,矩阵的0次幂就是单位阵,-1次幂就是对应的逆矩阵

12.3 矩阵方程和行列式求解
- solve功能对应于求解矩阵对应的解
- Det行列式代表一个数值
- Det数学含义,对于二阶矩阵,它就是一个面积,对于三阶矩阵,它就是一个体积,对于n维矩阵,就是n维立体的体积
关于矩阵方程及行列式的基本概念也可以查看之前关于线性代数的博客梳理,求解矩阵方程,比如方程的样式如下
{ 3 x 1 + x 2 = 9 x 1 + 2 x 2 = 8 ⇒ ( 3 1 1 2 ) ⇒ ( 9 8 ) \begin{cases} 3x_{1} +x_{2}=9 \\ x_{1} + 2x_{2}=8\\ \end{cases} \Rightarrow \left(\begin{matrix} 3&1\\1&2\end{matrix}\right) \Rightarrow\left(\begin{matrix} 9\\8\end{matrix}\right) { 3x1+x2=9x1+2x2=8⇒(3112)⇒(98)

那随便再进行一个验证,代码如下,复杂点的,随便找的数值

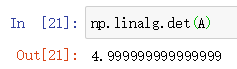
最后进行行列式的计算,这个就是线性代数里面的考试必考题了,直接通过np.linalg.det(A)进行计算,之前在梳理线性代数的知识点的时候为了确保手算的准确性已经有用过python辅助代码验证
13 Numpy中条件逻辑表述为数组运算
np.where()函数是三元表达式x if condition else y的⽮量化版本。假设我们有⼀个布尔数组和两个值数组,如下。我们想要根据cond中的值选取xarr和yarr的值:当cond中的值为True时,选取xarr的值,否则从yarr中选取。列表推导式的写法应该如下所示:

这有⼏个问题。第⼀,它对⼤数组的处理速度不是很快(因为所有⼯作都是由纯Python完成的)。第⼆,⽆法⽤于多维数组。若使⽤np.where,则可以将该功能写得⾮常简洁:直接一步到位

np.where的第⼆个和第三个参数不必是数组,它们都可以是标量值。在数据分析⼯作中,where通常⽤于根据另⼀个数组⽽产⽣⼀个新的数组。假设有⼀个由随机数据组成的矩阵,你希望将所有正值替换为2,将所有负值替换为-2。若利⽤np.where,则会⾮常简单

np.where方法在今后的数据分析中结合pands进行数据处理还是很使用的,功能比较强大,比replace要厉害的多,至此整个numpy的常用知识点就梳理完毕了,还有一些统计函数以及数据读取的内容就没有必要梳理了,这部分会在pands中有更好的处理方式。