人工智能-机器学习：模型调优【交叉验证、网格搜索(可并行计算)、启发式搜索(随机搜索,遗传算法,贝叶斯优化)】、模型评估【准确率、精确率、召回率、F1-Measure、ROC/AUC】、AIC、BIC

一、模型调优

1、交叉验证

交叉验证是一种通过估计模型的泛化误差，从而进行模型选择的方法。没有任何假定前提，具有应用的普遍性，操作简便， 是一种行之有效的模型选择方法。

1.1 交叉验证的产生

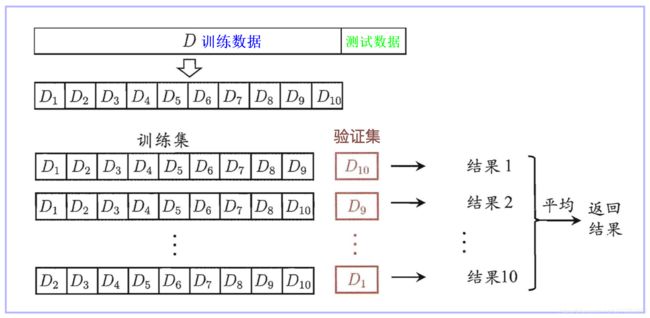
人们发现用同一数据集，既进行训练，又进行模型误差估计，对误差估计的很不准确，这就是所说的模型误差估计的乐观性。为了克服这个问题，提出了交叉验证。基本思想是将数据分为两部分，一部分数据用来模型的训练，称为训练集；另外一部分用于测试模型的误差，称为验证集。由于两部分数据不同，估计得到的泛化误差更接近真实的模型表现。数据量足够的情况下，可以很好的估计真实的泛化误差。但是实际中，往往只有有限的数据可用，需要对数据进行重用，从而对数据进行多次切分，得到好的估计。

1.2 交叉验证方法

1. 留一交叉验证（leave-one-out）：每次从个数为N的样本集中，取出一个样本作为验证集，剩下的N-1个作为训练集，重复进行N次。最后平均N个结果作为泛化误差估计。
2. 留P交叉验证（leave-P-out）：与留一类似，但是每次留P个样本。每次从个数为N的样本集中，取出P个样本作为验证集，剩下的N-P个作为训练集，重复进行CPNCNP次。最后平均N个结果作为泛化误差估计。
   以上两种方法基于数据完全切分，重复次数多，计算量大。因此提出几种基于数据部分切分的方法减轻计算负担。
3. K-折交叉验证：把数据分成K份，每次拿出一份作为验证集，剩下k-1份作为训练集，重复K次。最后平均K次的结果，作为误差评估的结果。与前两种方法对比，只需要计算k次，大大减小算法复杂度，被广泛应用。
   • 将原始数据分为训练数据与测试数据，训练数据是交给工程师用于生成模型用的。
   • 测试数据一般是客户用来检查模型质量的数据，一般不会给工程师。
   • 工程师手里的训练数据，分为训练集和验证集。以下图为例：将数据分成10份(一般分为10份)，其中一份作为验证集。然后经过10次(组)的测试，每次都更换不同的验证集。即得到10组模型的结果，取平均值作为最终结果。又称 十折交叉验证。
     
     交叉验证目的：为了让被评估的模型更加准确可信。
     

1.3 模型选择方法的评价

衡量一个模型评估方法的好坏，往往从偏差和方差两方面进行。

1.3.1 偏差

交叉验证只用了一部分数据用于模型训练，相对于足够多的数据进行训练的方法来说，模型训练的不充分，导致误差估计产生偏差。

• 相对来说，留一交叉验证，每次只留下一个作为验证集，其余数据进行训练，产生泛化误差估计结果相对真值偏差较小。很多文献表明留一交叉验证在回归下的泛化误差估计是渐进无偏的。
• 留P交叉验证，取决于P的大小，P较小时，等同于留一交叉验证的情况。P较大，会产生较大的偏差，不可忽略。
• K折交叉验证，同样取决于K的大小。K较大时，类似留一交叉验证；K较小时，会产生不可忽略的偏差。

训练数据越小，偏差越大。当偏差无法忽略时，需要对偏差进行纠正。

1.3.2 方差

• 对于一个模型，训练数据固定后，不同的验证集得到的泛化误差评估结果的波动，称之为误差评估的方差。
• 影响方差变化的因素，主要有数据的切分方法，模型的稳定性等。
• 训练数据固定的情况下，验证集中样本数量越多，方差越小。
• 模型的稳定性是指模型对于数据微小变化的敏感程度。

1.4 针对K-折交叉验证的 $k$ 的选择，及偏差和方差分析

• 对于 $k$ 的选择，实践中一般取 $k=10$。
• 当 $k=N$时，(N为训练样本数量)，$k$ 折交叉验证退化为留一交叉验证（leave-one-out cross validation）。由于在留一交叉验证中，每一次训练模型的样本几乎是一样的，这样就会造成估计的偏差很小但方差很大的情况出现，另外，需要调用 $N$ 次学习算法，这在 $N$ 很大的时候，对于计算量也是不小的开销。
• 如果取 $k=10$，那么交叉验证的方差会降低，但是偏差又相对于 $k=N$ 时增大，这取决于训练样本的数量。当训练样本较小时，交叉验证很容易有较高的偏差，但是随着训练样本的增加，这种情况会得到改善。

问题：这个只是让被评估的模型更加准确可信，那么怎么选择或者调优参数呢？使用网格搜索。

1.5 单一“超参数”调优：cross_val_score

import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score

# model_selection:模型选择
# cross_val_score  cross：交叉，validation：验证（测试）
# 交叉验证
if __name__ == "__main__":
    # 一、数据加载
    X, y = datasets.load_iris(True)
    print('X.shape = ', X.shape)
    # cross_val_score交叉验证删选最合适参数
    # 二、交叉验证
    # 2.1 实例化k-近邻估计器
    knn = KNeighborsClassifier()
    # 2.1 实例化k-近邻估计器
    # 2.2 应用cross_val_score筛选最合适的邻居数量
    erros = []
    for k in range(1, 14):
        knn = KNeighborsClassifier(n_neighbors=k)
        score = cross_val_score(knn, X, y, scoring='accuracy', cv=6).mean()
        #   误差越小，说明k选择越合适，越好
        erros.append(1 - score)
    # 2.3 画图
    plt.plot(np.arange(1, 14), erros)   # 从图中可看出：k = 11时，误差最小，说明k = 11对鸢尾花来说，最合适的k值

    # 2.4 参数调节：多参数组合使用cross_val_score筛选最合适的参数组合
    result = {
     }
    weights = ['uniform', 'distance']
    for k in range(1, 14):
        for w in weights:
            knn = KNeighborsClassifier(n_neighbors=k, weights=w)
            sm = cross_val_score(knn, X, y, scoring='accuracy', cv=6).mean()
            result[w + str(k)] = sm
    print('result = ', result)
    max_value_index = np.array(list(result.values())).argmax()
    print('max_value_index = ', max_value_index)
    result_list = list(result)
    print('result_list = ', result_list)
    print('result_list[max_value_index] = ', result_list[max_value_index])

打印结果：

X.shape =  (150, 4)
result =  {
     
'uniform1': 0.9591049382716049,
'distance1': 0.9591049382716049,
'uniform2': 0.9390432098765431,
'distance2': 0.9591049382716049,
'uniform3': 0.9660493827160493,
'distance3': 0.9660493827160493,
'uniform4': 0.9660493827160493,
'distance4': 0.9660493827160493,
'uniform5': 0.9660493827160493,
'distance5': 0.9660493827160493,
'uniform6': 0.9729938271604938,
'distance6': 0.9729938271604938,
'uniform7': 0.9729938271604938,
'distance7': 0.9729938271604938,
'uniform8': 0.9591049382716049,
'distance8': 0.9729938271604938,
'uniform9': 0.9660493827160493,
'distance9': 0.9729938271604938,
'uniform10': 0.9729938271604938,
'distance10': 0.9729938271604938,
'uniform11': 0.98070987654321,
'distance11': 0.9799382716049383,
'uniform12': 0.9737654320987654,
'distance12': 0.9799382716049383,
'uniform13': 0.9737654320987654,
'distance13': 0.9729938271604938
}
max_value_index =  20
result_list =  [
'uniform1',
'distance1',
'uniform2',
'distance2',
'uniform3',
'distance3',
'uniform4',
'distance4',
'uniform5',
'distance5',
'uniform6',
'distance6',
'uniform7',
'distance7',
'uniform8',
'distance8',
'uniform9',
'distance9',
'uniform10',
'distance10',
'uniform11',
'distance11',
'uniform12',
'distance12',
'uniform13',
'distance13'

]
result_list[max_value_index] =  uniform11

2、多“超参数”组合调优：网格搜索

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
对估计器的指定参数值进行详尽搜索(排列组合，然后找出使得模型效果最好的最优参数组合)

比如，模型需要超参数(a,b)。给这参数a指定2个待评估参数3,7，给参数b指定3个待评估参数20,36,72，那么模型会对(3,20)、(3,36)、(3,72)、(7,20)、(7,36)、(7,72)这几组参数分别评估，然后通过准确率选出一个最优的参数组合来建立模型。

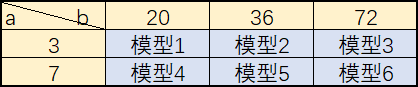
超参数调优-网格搜索Api：sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

• estimator：估计器对象
• param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
• cv：指定几折交叉验证
• fit：输入训练数据
• score：准确率

结果分析：

• best_score_:在交叉验证中测试的最好结果
• best_estimator_：最好的参数模型
• cv_results_:每次交叉验证后的验证集准确率结果和训练集准确率结果

import pandas as pd
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier


def knncls():
    """K-近邻预测用户签到位置"""
    # 1、读取数据(pandas)
    myDataFrame = pd.read_csv("I:/AI_Data/facebook-v-predicting-check-ins/train.csv")
    print('\nmyDataFrame.head(5) = \n', myDataFrame.head(5))

    # 2、处理数据(pandas)
    # 2.1 缩小数据,查询数据晒讯
    myDataFrame = myDataFrame.sort_values(by='row_id').query("x > 1.0 &  x < 1.25 & y > 2.5 & y < 2.75")
    print('\nmyDataFrame.count() = \n', myDataFrame.count())
    # 处理时间的数据：将时间戳转换为Series类型(格式为：index=时间戳, value=yyyy-mm-dd hh:mm:ss)
    dateTimeSeries = pd.to_datetime(myDataFrame['time'], unit='s')
    print('\ntype(dateTimeSeries) = ', type(dateTimeSeries))
    print('\ndateTimeSeries.head(5) = \n', dateTimeSeries.head(5))
    # 2.2 把dateTimeSeries转换成DatetimeIndex索引(字典类型)
    dateTimeIndexMap = pd.DatetimeIndex(dateTimeSeries)
    print('\ntype(dateTimeIndexMap) = ', type(dateTimeIndexMap))
    print('\ndateTimeIndexMap = \n', dateTimeIndexMap)
    # 2.3 构造一些特征(添加某些特征有可能会使预测准确度增加或减小)
    # myDataFrame['year'] = dateTimeIndexMap.year   # 年份没有意义，因为以后的预测不可能重复此年份
    myDataFrame['month'] = dateTimeIndexMap.month
    myDataFrame['day'] = dateTimeIndexMap.day
    myDataFrame['hour'] = dateTimeIndexMap.hour
    # myDataFrame['minute'] = dateTimeIndexMap.minute
    # myDataFrame['weekday'] = dateTimeIndexMap.weekday
    # 2.4 把时间戳特征删除
    myDataFrame = myDataFrame.drop(['time'], axis=1)
    print('\nmyDataFrame.head(5) = \n', myDataFrame.head(5))
    # 2.5 把签到数量少于n个目标位置删除
    # 分组然后统计每组数量，分组后place_id变为索引，其余特征的特征值变为当前分组下的成员数量
    placeCountDataFrame = myDataFrame.groupby('place_id').count()
    print('\ntype(placeCountDataFrame) = \n', type(placeCountDataFrame))
    print('\nplaceCountDataFrame = \n', placeCountDataFrame.head(5))
    # 选取组成员数量大于3的分组，然后通过reset_index将原来的索引place_id变为一列可以被引用的特征place_id，新索引变为0,1,2,3...
    placeCountDataFrame = placeCountDataFrame[placeCountDataFrame.row_id > 3].reset_index()  # 选择每组数量大于3的样本
    print('\nplaceCountDataFrame = \n', placeCountDataFrame.head(5))
    # 根据placeCountDataFrame里的place_id筛选myDataFrame中符合条件的样本
    myDataFrame = myDataFrame[myDataFrame['place_id'].isin(placeCountDataFrame.place_id)]
    print('\nmyDataFrame.head(5) = \n', myDataFrame.head(5))
    # 2.6 将数据当中的特征值和目标值分开
    y_Series = myDataFrame['place_id']  # 目标值
    x_DataFrame = myDataFrame.drop(['place_id'], axis=1)  # 特征值
    # 2.7 删除特征值里没有用的特征，来提高准确率
    x_DataFrame = x_DataFrame.drop(['row_id'], axis=1)
    print('\ny_Series = \n', type(y_Series), '\n', y_Series.head(5))
    print('\nx_DataFrame = \n', type(x_DataFrame), '\n', x_DataFrame.head(5))

    # 3、特征工程(scikit-learn)
    # 3.1 特征预处理(特征数据值的标准化，目标值不需要标准化)，避免某一特征对最终结果造成比其他特征更大的影响，从而提高准确率。
    std = StandardScaler()
    x_DataFrame = std.fit_transform(x_DataFrame)
    print('\n标准化后的x_DataFrame：\n', x_DataFrame)
    # 3.2 进行数据的分割：训练集、测试集
    x_train_DataFrame, x_test_DataFrame, y_train_Series, y_test_Series = train_test_split(x_DataFrame, y_Series, test_size=0.25)
    print('\n特征数据值of训练集 x_train_DataFrame：\n', x_train_DataFrame)
    print('\n特征数据值of测试集 x_test_DataFrame：\n', x_test_DataFrame)
    print('\n目标值of训练集 y_train_Series：\n', y_train_Series.head(5))
    print('\n目标值of测试集 y_test_Series：\n', y_test_Series.head(5))

    # 4 算法工程
    # 4.1 实例化一个k-紧邻估计器对象
    knn_estimator = KNeighborsClassifier()  # 默认参数：n_neighbors=5
    # # 4.2 调用fit方法,进行训练
    # knn_estimator.fit(x_train_DataFrame, y_train_Series)
    # # 5 模型评估
    # # 5.1 数据预测，得出预测结果
    # predictTestSeries = knn_estimator.predict(x_test_DataFrame)
    # # 5.2 计算准确率
    # predictScore = knn_estimator.score(x_test_DataFrame, y_test_Series)  # 输入”测试集“的特征数据值、目标值

    # 网格搜索进行超参数调优(代替上述步骤4.2 & 5.1 & 5.2)
    # 构造一些参数的值进行搜索
    param = {
     "n_neighbors": [3, 5, 10]}
    gc = GridSearchCV(knn_estimator, param_grid=param, cv=2)    # 一般设置cv=10
    gc.fit(x_train_DataFrame, y_train_Series)  # 输入”训练集“的特征数据值、目标值
    # 模型评估
    print("设定的超参数n_neighbors: [3, 5, 10]分别交叉验证(cv=2,共2次交叉验证)的结果，cv_results_：\n", gc.cv_results_)
    print("在交叉验证当中准确率最好的结果best_score_：", gc.best_score_)
    print("选择最好的模型best_estimator_ = ", gc.best_estimator_)
    print("在测试集上准确率score() =", gc.score(x_test_DataFrame, y_test_Series))


if __name__ == "__main__":
    knncls()

打印结果：

myDataFrame.head(5) = 
    row_id       x       y  accuracy    time    place_id
0       0  0.7941  9.0809        54  470702  8523065625
1       1  5.9567  4.7968        13  186555  1757726713
2       2  8.3078  7.0407        74  322648  1137537235
3       3  7.3665  2.5165        65  704587  6567393236
4       4  4.0961  1.1307        31  472130  7440663949
myDataFrame.count() = 
 row_id      17710
x           17710
y           17710
accuracy    17710
time        17710
place_id    17710
dtype: int64
type(dateTimeSeries) =  <class 'pandas.core.series.Series'>
dateTimeSeries.head(5) = 
 600    1970-01-01 18:09:40
957    1970-01-10 02:11:10
4345   1970-01-05 15:08:02
4735   1970-01-06 23:03:03
5580   1970-01-09 11:26:50
Name: time, dtype: datetime64[ns]
type(dateTimeIndexMap) =  <class 'pandas.core.indexes.datetimes.DatetimeIndex'>
dateTimeIndexMap = 
 DatetimeIndex(['1970-01-01 18:09:40', '1970-01-10 02:11:10',
               '1970-01-05 15:08:02', '1970-01-06 23:03:03',
               '1970-01-09 11:26:50', '1970-01-02 16:25:07',
               '1970-01-04 15:52:57', '1970-01-01 10:13:36',
               '1970-01-09 15:26:06', '1970-01-08 23:52:02',
               ...
               '1970-01-07 10:03:36', '1970-01-09 11:44:34',
               '1970-01-04 08:07:44', '1970-01-04 15:47:47',
               '1970-01-08 01:24:11', '1970-01-01 10:33:56',
               '1970-01-07 23:22:04', '1970-01-08 15:03:14',
               '1970-01-04 00:53:41', '1970-01-08 23:01:07'],
              dtype='datetime64[ns]', name='time', length=17710, freq=None)
myDataFrame.head(5) = 
       row_id       x       y  accuracy    place_id  month  day  hour
600      600  1.2214  2.7023        17  6683426742      1    1    18
957      957  1.1832  2.6891        58  6683426742      1   10     2
4345    4345  1.1935  2.6550        11  6889790653      1    5    15
4735    4735  1.1452  2.6074        49  6822359752      1    6    23
5580    5580  1.0089  2.7287        19  1527921905      1    9    11
type(placeCountDataFrame) = 
 <class 'pandas.core.frame.DataFrame'>
placeCountDataFrame = 
             row_id     x     y  accuracy  month   day  hour
place_id                                                   
1012023972       1     1     1         1      1     1     1
1057182134       1     1     1         1      1     1     1
1059958036       3     3     3         3      3     3     3
1085266789       1     1     1         1      1     1     1
1097200869    1044  1044  1044      1044   1044  1044  1044
placeCountDataFrame = 
      place_id  row_id     x     y  accuracy  month   day  hour
0  1097200869    1044  1044  1044      1044   1044  1044  1044
1  1228935308     120   120   120       120    120   120   120
2  1267801529      58    58    58        58     58    58    58
3  1278040507      15    15    15        15     15    15    15
4  1285051622      21    21    21        21     21    21    21
myDataFrame.head(5) = 
       row_id       x       y  accuracy    place_id  month  day  hour
600      600  1.2214  2.7023        17  6683426742      1    1    18
957      957  1.1832  2.6891        58  6683426742      1   10     2
4345    4345  1.1935  2.6550        11  6889790653      1    5    15
4735    4735  1.1452  2.6074        49  6822359752      1    6    23
5580    5580  1.0089  2.7287        19  1527921905      1    9    11
y_Series = 
 <class 'pandas.core.series.Series'> 
 600     6683426742
957     6683426742
4345    6889790653
4735    6822359752
5580    1527921905
Name: place_id, dtype: int64
x_DataFrame = 
 <class 'pandas.core.frame.DataFrame'> 
            x       y  accuracy  month  day  hour
600   1.2214  2.7023        17      1    1    18
957   1.1832  2.6891        58      1   10     2
4345  1.1935  2.6550        11      1    5    15
4735  1.1452  2.6074        49      1    6    23
5580  1.0089  2.7287        19      1    9    11
标准化后的x_DataFrame：
 [[ 1.27892477  0.9941573  -0.58835492  0.         -1.50340614  0.94055369]
 [ 0.78467442  0.80524744 -0.21403874  0.          1.80968818 -1.36413448]
 [ 0.91794088  0.31723029 -0.6431329   0.         -0.03091978  0.50842466]
 ...
 [-1.27513331  1.3018514  -0.17752009  0.          1.07344499  0.50842466]
 [ 1.04344424  0.66928958  0.05072149  0.         -0.39904137 -1.65222051]
 [-0.20123858 -1.30138377  0.88152082  0.          1.07344499  1.66076875]]
特征数据值of训练集 x_train_DataFrame：
 [[ 1.15600911 -1.65630533 -0.69791088  0.         -0.76716296  0.22033864]
 [ 0.94381786  0.80667857 -0.23229806  0.          0.33720181  0.94055369]
 [-0.00845506 -0.034829    1.24670734  0.         -1.13528455  0.36438165]
 ...
 [-0.36814511 -0.24091249 -0.14100143  0.         -1.50340614 -0.35583341]
 [ 1.46653289  1.51079716 -0.25055739  0.          0.7053234   0.22033864]
 [ 0.39263815  0.43887679 -0.08622346  0.         -0.76716296 -1.5081775 ]]
特征数据值of测试集 x_test_DataFrame：
 [[ 1.41477892  0.62778666 -0.16839042  0.          0.33720181  0.07629563]
 [-1.24666863  0.61633757 -0.56096593  0.         -1.13528455 -1.5081775 ]
 [-0.42119292 -1.54753905 -0.7161702   0.         -1.50340614  0.79651068]
 ...
 [-1.52355234  1.49791694 -0.70704054  0.          1.44156658 -1.36413448]
 [ 0.14292528 -0.73751645 -0.1501311   0.          0.7053234   0.79651068]
 [-1.13539761 -0.73608531 -0.06796413  0.          1.44156658  1.66076875]]
目标值of训练集 y_train_Series：
 2157968     8695574026
11153682    8258328058
8086959     5606572086
304429      2355236719
14884334    6502303487
Name: place_id, dtype: int64
目标值of测试集 y_test_Series：
 29084739    2327054745
12213699    3312463746
15897007    6399991653
15606379    3533177779
997179      1228935308
Name: place_id, dtype: int64

设定的超参数n_neighbors: [3, 5, 10]分别交叉验证(cv=2,共2次交叉验证)的结果，cv_results_：
 {
     
 'mean_fit_time': array([0.00499177, 0.00400281, 0.00498641]), 
 'std_fit_time': array([1.19209290e-06, 1.35898590e-05, 3.57627869e-07]), 
 'mean_score_time': array([0.17004263, 0.19496608, 0.19624221]), 
 'std_score_time': array([0.00249135, 0.01743865, 0.00222671]), 
 'param_n_neighbors': masked_array(data=[3, 5, 10],mask=[False, False, False],fill_value='?', dtype=object), 
 'params': [{
     'n_neighbors': 3}, {
     'n_neighbors': 5}, {
     'n_neighbors': 10}], 
 'split0_test_score': array([0.43350524, 0.45913424, 0.46726051]), 
 'split1_test_score': array([0.4326602 , 0.46668787, 0.47877246]), 
 'mean_test_score': array([0.43308638, 0.46287831, 0.47296658]), 
 'std_test_score': array([0.0004225 , 0.00377667, 0.00575576]), 
 'rank_test_score': array([3, 2, 1]), 
 'split0_train_score': array([0.65034187, 0.60740976, 0.55271108]), 
 'split1_train_score': array([0.65353962, 0.60571964, 0.54852321]), 
 'mean_train_score': array([0.65194074, 0.6065647 , 0.55061714]), 
 'std_train_score': array([0.00159887, 0.00084506, 0.00209394])
 }
在交叉验证当中准确率最好的结果best_score_： 0.4729665825977301
选择最好的模型best_estimator_ = KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski', metric_params=None, n_jobs=1, n_neighbors=10, p=2, weights='uniform')
在测试集上准确率score() = 0.502127659574468

3、网格搜索 V.S. 启发式搜索

• 网格搜索虽然简单，但是可并行计算，
• 启发式搜索不容易并行，并且寻找最优路径也很花时间

二、模型评估

机器学习(ML)，自然语言处理(NLP)，信息检索(IR)等领域，评估(Evaluation)是一个必要的工作。

1、混淆矩阵

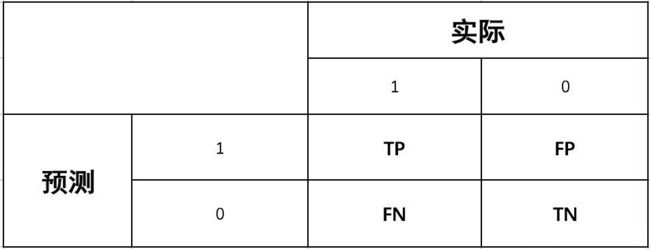
对于二分类的模型，预测结果与实际结果分别可以取0和1。我们用N和P代替0和1，T和F表示预测正确和错误。将他们两两组合，就形成了下图所示的混淆矩阵（注意：组合结果都是针对预测结果而言的）。

由于1和0是数字，阅读性不好，所以我们分别用P和N表示1和0两种结果。变换之后为PP，PN，NP，NN，阅读性也很差，我并不能轻易地看出来预测的正确性与否。因此，为了能够更清楚地分辨各种预测情况是否正确，我们将其中一个符号修改为T和F，以便于分辨出结果。

• P（Positive）：代表 1
• N（Negative）：代表 0
• T（True）：代表预测正确
• F（False）：代表预测错误

分类算法模型评价指标往往有如下几个：

• 准确率(Accuracy)
• 精确率(Precision)
• 召回率(Recall)
• F1-Measure

评估工作中具体要用哪个指标进行评估得根据实际情景来定。比如文章分类就没必要用召回率。

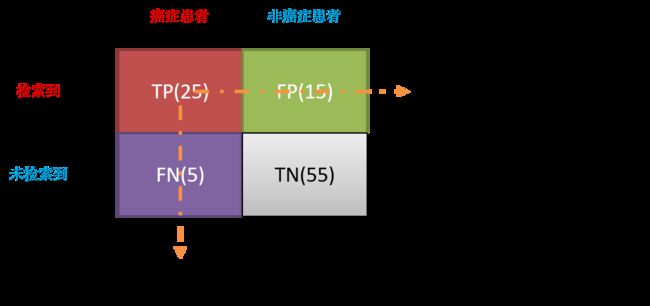
假定一个具体场景作为例子：医生A要检测一款新的癌症检测仪器的性能

$\boxed{实验组：一共100个病人样本。真实情况是：癌症患者30人，非癌症患者70人}$
$\boxed{目标：找出所有癌症患者。}$
$\boxed{实验结果：仪器总共检测出40人患有癌症，医生A发现这40人中25人是癌症患者，15人是非癌症患者。}$

• 准确率(Accuracy)：对于给定的测试数据集，分类器正确分类的样本数与总样本数之比。
  $$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
• 精确率(Precision)**：计算的是所有"正确被检索的item(TP)"占所有"实际被检索到的(TP+FP)"的比例。
  $$Precision=\frac{TP}{TP+FP}$$
• 召回率(Recall)：计算的是所有"正确被检索的item(TP)"占所有"应该检索到的item(TP+FN)"的比例。
  $$Recall=\frac{TP}{TP+FN}$$
• F1-Measure值：就是精确率和召回率的调和平均值。
  $$\begin{array}{r}F1-Measure=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}}\end{array}$$

仪器性能测试结果：

• 仪器诊断错误的数量为15人，总人数为100人。所以准确率(Accuracy) $=\frac{100-15}{100}=85\%$；
• 仪器共诊断(或检索)出40人，其中25人是被正确的诊断，精确率(Precision) $=\frac{25}{40}=62.5\%$；
• 仪器共正确地诊断(或检索)出25人是癌症患者，而癌症患者一共有30人，所以，召回率(Recall) $=\frac{25}{30}=83.3\%$；
• $\begin{array}{r}F1-Measure=\frac{2}{\frac{TP+FP}{TP}+\frac{TP+FN}{TP}}=\frac{2\cdot TP}{2\cdot TP+FP+FN}=\frac{2\times 25}{2\times 25+15+5}=71.4\%\end{array}$

2、ROC/AUC

• 灵敏度（Sensitivity）：实际为正样本预测成正样本的概率
  $$Sensitivity=\frac{TP}{TP+FN}$$
• 特异度（Specificity）：即实际为负样本预测成负样本的概率
  $$Recall=\frac{TN}{FP+TN}$$
• 真正例率（TPR） = 灵敏度 ：实际为正样本预测成正样本的概率
  $$TPR=\frac{TP}{TP+FN}$$
• 假正例率（FPR） = 1- 特异度：实际为负样本预测成正样本的概率
  $$FPR=\frac{FP}{FP+TN}$$
• 召回率 = 灵敏度 = 查全率 = 真正率 = $TPR=\frac{TP}{TP+FN}$，都是指：实际正样本中预测为正样本的概率
• 我们可以看出：
  • 真正率和假正率这两个指标跟正负样本的比例是无关的
  • 所以当样本比例失衡的情况下，准确率不如真正率、假正率这两个指标好用

2.1 ROC（Receiver Operating Characteristic）曲线

ROC（Receiver Operating Characteristic）曲线，又称接受者操作特征曲线。

• 真正例率（Ture Positive Rare），$TPR=\frac{TP}{TP+FN}$ 是ROC曲线的纵轴
• 假正例率（False Positive Rare），$FPR=\frac{FP}{FP+TN}$ 是ROC曲线的横轴

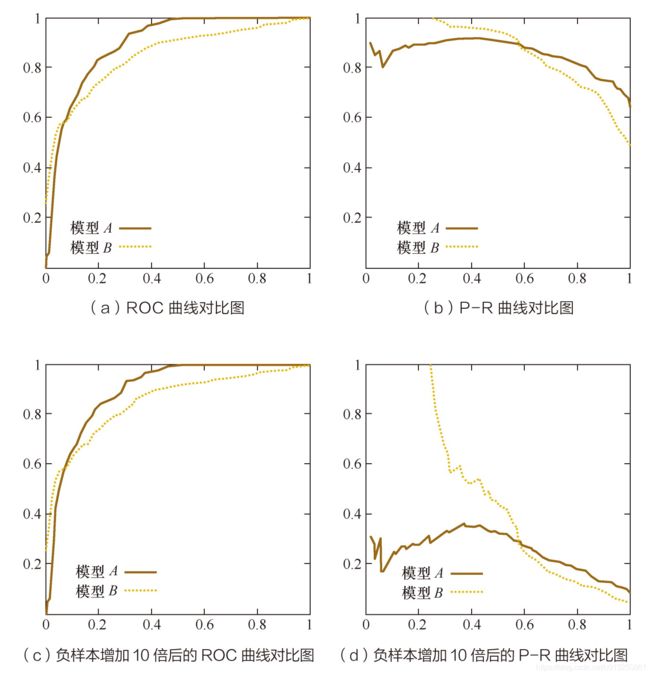
既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比：

在上图中，(a)和©为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，©和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。

2.2 AUC值

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。

又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。

使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

2.3 代码实现ROC/AUC

from sklearn import metrics
from sklearn.metrics import auc 
import numpy as np
y = np.array([1, 1, 2, 2])  
scores = np.array([0.1, 0.4, 0.35, 0.8])  
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
metrics.auc(fpr, tpr) 

0.75

3、AIC/BIC准则

经常地，对一堆数据进行建模的时候，特别是分类和回归模型，我们有很多的变量可供使用，选择不同的变量组合可以得到不同的模型，例如我们有5个变量，2的5次方，我们将有32个变量组合，可以训练出32个模型。但是哪个模型更加的好呢？目前常用有如下方法：

赤池信息量 akaike information criterion：$AIC=-2ln(L)+2k$

贝叶斯信息量 bayesian information criterion：$BIC=-2ln(L)+ln(n)\times k$

L是在该模型下的最大似然，n是数据数量，k是模型的变量个数

三个模型A, B, C，在通过这些规则计算后，我们知道B模型是三个模型中最好的，但是不能保证B这个模型就能够很好地刻画数据，因为很有可能这三个模型都是非常糟糕的，B只是烂苹果中的相对好的苹果而已。

这些规则理论上是比较漂亮的，但是实际在模型选择中应用起来还是有些困难的，我们不可能对所有这些模型进行一一验证AIC, BIC，HQ规则来选择模型，工作量太大。

3.1 AIC准则

赤池信息量准则，即Akaike information criterion、简称AIC，是衡量统计模型拟合优良性的一种标准，是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在熵的概念基础上。

AIC越小，模型越好，通常选择AIC最小的模型

3.2 BIC准则

---

---

---

参考资料：
【机器学习笔记】：一文让你彻底记住什么是ROC/AUC（看不懂你来找我）
精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？
ROC、AUC、经验误差和估计方法
详解ROC/AUC计算过程
机器学习：图文详解模型评估指标ROC/AUC
模型选择方法：AIC和BIC