数据结构与算法学习②(栈,队列,面试题)
栈,队列,面试题
- 栈
-
- 存储结构及特点
- 栈的实现
-
- 基于数组来实现栈
- 基于链表实现栈
- 总结
- 栈的面试题
-
- 哔哩哔哩,小米最近面试题,20. 有效的括号
- 亚马逊,字节跳动,腾讯最近面试题,155. 最小栈
- 队列
-
- 存储结构及特点
- 队列的实现
-
- java API
- 基于链表实现队列
- 基于数组实现队列
- 小结
- 实战
-
- 622. 设计循环队列
- 641. 设计循环双端队列
- 703. 数据流中的第K大元素
- 栈和队列面试题
-
- 腾讯,字节跳动最近面试题,232. 用栈实现队列
- 字节跳动,facebook最近面试题,225. 用队列实现栈
- 华为,网易,腾讯最近面试题,84. 柱状图中最大的矩形(重点)
- 字节跳动,华为,腾讯最近面试题,42. 接雨水
- 字节跳动,谷歌,亚马逊最近面试题,239. 滑动窗口最大值
栈
存储结构及特点
“栈(Stack)”并非指某种特定的数据结构,它是有着相同典型特征的一类数据结构的统称,因为栈可以用数组实现,也可以用链表实现。该典型特征是:后进先出;英文表示为:Last In First Out即LIFO,只要满足这种特点的数据结构我们就可以说这是栈,为了更好的理解栈这种数据结构,我们以一幅图的形式来表示,如下:

我们从栈的操作特点上来看,栈就是一种操作受限的线性表,只允许在栈的一端进行数据的插入和删除,这两种操作分别叫做入栈(push)和出栈(pop),时间复杂度均为O(1)
知识小贴士:
1:此处讲的栈和java语言中讲到的栈空间不是一回事,此处的栈指的是一种数据,而java语言中的栈空间指的是java内存结构的一种表示,不能等同
2:相比于数组和链表来说,栈的数据操作受到了限制,那我们直接用数组或链表不就可以了么,为什么还要使用栈呢?
当某个数据集合如果只涉及到在其一端进行数据的插入和删除操作,并且满足先进后出,后进先出的特性时,我们应该首选栈这种数据结构来进行数据的存储。
栈的实现
栈既可以用数组来实现,也可以用链表来实现。用数组实现的栈叫顺序栈,用链表实现的叫链式栈。对于栈的操作行为我们可以定义如下
/** * 返回栈中元素个数 * @return */
public int size() {
return 0;
}
/** * 判断栈是否为空 * @return */
public boolean empty() {
return false;
}
/** * 将元素压入栈 * @param item 被存入栈的元素 * @return */
public E push(E item) {
return item;
}
/** * 获取栈顶元素,但并不移除,如果栈空则返回null * @return */
public E peek() {
return null;
}
/** * 移除栈顶元素并返回,如果栈为空则返回null * @return */
public E pop() {
return null;
}
基于数组来实现栈
public class Stack<E> {
//维护一个数组存储数据
Object[] elementData;
//定义栈中元素的个数
int elementCount;
public Stack(int capacity) {
if (capacity < 0) {
throw new IllegalArgumentException("argument error,capacity="+capacity);
}
elementData = new Object[capacity];
}
public Stack() {
this(10);
}
/**
* 返回栈中元素个数
* @return
*/
public int size() {
return elementCount;
}
/**
* 判断栈是否为空
* @return
*/
public boolean isEmpty() {
return elementCount ==0;
}
/**
* 将元素压入栈
* @param item 被存入栈的元素
* @return
*/
public E push(E item) {
//检查容量,容量不够我们要先扩容
ensureCapactiy(elementCount+1);
this.elementData[elementCount] = item;
elementCount++;
return item;
}
private void ensureCapactiy(int minCapacity) {
if (minCapacity - this.elementData.length > 0) {
//扩容
grow(minCapacity);
}
}
private void grow(int minCapacity) {
int oldCapacity = this.elementData.length;
int newCapactiy = oldCapacity + (oldCapacity >>1);
if (newCapactiy < minCapacity) {
newCapactiy = minCapacity;
}
//实现扩容;按照新的容量创建一个新数组,将老数组中的数据拷贝过来
this.elementData = Arrays.copyOf(this.elementData,newCapactiy);
}
/**
* 获取栈顶元素,但并不移除,如果栈空则返回null
* @return
*/
public E peek() {
int len = size();
if (len ==0) {
return null;
}
return elementAt(len-1);
}
private E elementAt(int index) {
//检查索引范围
if (index < 0 || index>=elementCount) {
throw new IndexOutOfBoundsException("index out of bound,index="+index);
}
return (E) this.elementData[index];
}
/**
* 移除栈顶元素并返回,如果栈为空则返回null
* @return
*/
public E pop() {
//先得到栈顶元素
E peek = peek();
//删除栈顶元素即可
int len = size(); // len-1
removeElementAt(len-1);
return peek;
}
private void removeElementAt(int index) {
//检查索引范围
//检查索引范围
if (index < 0 || index>=elementCount) {
throw new IndexOutOfBoundsException("index out of bound,index="+index);
}
if (index < this.elementCount -1) {
//挪动元素,将index索引后面的元素依次向前挪动,这是个通用方法,只是说调用的时候传了固定值
System.arraycopy(this.elementData,index+1,this.elementData,index,this.elementCount-index-1);
}
/*this.elementData[this.elementCount-1] = null;
this.elementCount--;*/
this.elementCount--;
this.elementData[this.elementCount] = null;
}
@Override
public String toString() {
//将栈中元素按照[1,2,3,4]形式打印
StringBuilder stringBuilder = new StringBuilder("[");
for (int i=0;i<this.elementCount;i++){
stringBuilder.append(this.elementData[i]).append(",");
}
return stringBuilder.append("]").toString();
}
}
测试代码
public static void main(String[] args) {
//创建栈
Stack stack = new Stack();
//元素入栈
stack.push(1);
stack.push(3);
stack.push(5);
stack.push(7);
System.out.println("栈中元素个数:"+stack.size()+",栈是否为空:"+stack.isEmpty());
System.out.println("打印输出栈:"+stack);
System.out.println("栈顶元素为:"+stack.peek());
System.out.println("元素出栈"+stack.pop());
System.out.println("打印输出栈"+stack);
}
基于链表实现栈
这里有个思想链表实现的时候head,添加的时候往后存即可,要栈顶的因为是先进后出,返回头完事,删除的时候头向后移动,断开指针,size–就可以
public class LinkedListStack<E> {
//栈中元素的个数
int size;
//维护链表的头节点
Node<E> head;
/**
* 返回栈中元素个数
* @return
*/
public int size() {
return size;
}
/**
* 判断栈是否为空
* @return
*/
public boolean isEmpty() {
return size ==0;
}
/**
* 将元素压入栈
* @param item 被存入栈的元素
* @return
*/
public E push(E item) {
Node<E> newNode = new Node<>(item,head);
head = newNode;
size++;
return item;
}
/**
* 获取栈顶元素,但并不移除,如果栈空则返回null
* @return
*/
public E peek() {
if (head == null) {
return null;
}
return head.val;
}
/**
* 移除栈顶元素并返回,如果栈为空则返回null
* @return
*/
public E pop() {
if (head == null) {
return null;
}
Node<E> h = head;
head = head.next;
h.next = null;
size--;
return h.val;
}
@Override
public String toString() {
//打印1->2->3->null格式的数据
StringBuilder sb = new StringBuilder();
Node curr = head;
while (curr!=null){
sb.append(curr.val).append("->");
curr = curr.next;
}
return sb.append("null").toString();
}
private static class Node<E> {
E val;
Node<E> next;
public Node(E val,Node<E> next) {
this.val = val;
this.next = next;
}
}
测试类
public static void main(String[] args) {
LinkedListStack stack = new LinkedListStack();
//元素入栈
stack.push(1);
stack.push(3);
stack.push(5);
stack.push(7);
System.out.println("栈中元素个数:"+stack.size()+",栈是否为空:"+stack.isEmpty());
System.out.println("打印输出栈:"+stack);
System.out.println("栈顶元素为:"+stack.peek());
System.out.println("元素出栈"+stack.pop());
System.out.println("打印输出栈"+stack);
}
总结
在java中对于栈这种数据结构已经有对应的实现了,List接口下不仅有我们之前讲到过的ArrayList和LinkedList集合类,还有一个Stack类,下面的图可以帮我们很清晰的看到List接口下的实现情况

Vector,Stack,ArrayList,LinkedList的比较
首先都实现List接口,而List接口一共有三个实现类,分别是ArrayList、Vector和LinkedList。List用于存放多个元素,能够维护元素的次序,并且允许元素的重复。3个具体实现类的相关区别如下:
1:ArrayList是最常用的List实现类,内部是通过数组实现的,它允许对元素进行快速随机访问。数组的缺点是每个元素之间不能有间隔,当数组大小不满足时需要增加存储能力,就要将已有数组的数据复制到新的存储空间中。当从ArrayList的中间位置插入或者删除元素时,需要对数组进行复制、移动、代价比较高。因此,它适合随机查找和遍历,不适合插入和删除。
2:Vector与ArrayList一样,也是通过数组实现的,不同的是它支持线程的同步,即某一时刻只有一个线程能够写Vector,避免多线程同时写而引起的不一致性,但实现同步需要很高的花费,因此,访问它比访问ArrayList慢。
3: LinkedList是用链表结构(双向链表)存储数据的,很适合数据的动态插入和删除,随机访问和遍历速度比较慢。
4:Vector和Stack是线程(Thread)同步(Synchronized)的,所以它也是线程安全的,而Arraylist是线程异步(ASynchronized)的,是不安全的。如果不考虑到线程的安全因素,一般用Arraylist效率比较高。
5:如果集合中的元素的数目大于目前集合数组的长度时,vector增长是按照 2*原数组大小,,而arraylist增长率为1.5 *原数组大小。如果在集合中使用数据量比较大的数据,用vector有一定的优势。
6:如果查找一个指定位置的数据,vector和arraylist使用的时间是相同的,都是0(1),这个时候使用vector和arraylist都可以。而如果移动一个指定位置的数据花费的时间为0(n),这个时候就应该考虑到使用Linkedlist,因为它移动一个指定位置的数据所花费的时间为0(1),而查询一个指定位置的数据时花费的时间为0(n)。ArrayList 和Vector是采用数组方式存储数据,此数组元素数大于实际存储的数据以便增加和插入元素,都允许直接序号索引元素,但是插入数据要设计到数组元素移动等内存操作,所以索引数据快插入数据慢,Vector由于使用了synchronized方法(线程安全)所以性能上比ArrayList要差,LinkedList使用双向链表实现存储,按序号索引数据需要进行向前或向后遍历,但是插入数据时只需要记录本项的前后项即可,所以插入数度较快.。
7:Stack是继承自Vector,底层也是基于数组实现的,只不过Stack插入和获取元素有一定的特点,满足后进先出的特点即LIFO,因此Stack也是我们所讲的典型的“栈”这种数据结构,且底层也支持动态扩容,其扩容方式和Vector,ArrayList底层扩容原理一样。Stack元素入栈和出栈的时间复杂度都是O(1)。
栈的面试题
哔哩哔哩,小米最近面试题,20. 有效的括号
https://leetcode-cn.com/problems/valid-parentheses/

用队列实现,因为队列是先进后出的,而括号要形成对子的话,比如{[]}这样的,1,4是对称,而2,3对称,满足先进后出的情况,先进去一个{再进去一个[,那出来下比较的时候需要先]再这个}这样才能对称.
把字符串转成数组,然后排出奇数的情况.遍历比较,如果出现左括号,就推入右括号进栈.当左括号进完了,只有右括号时,栈中先出来的括号和最近的括号是否一致,如果一致就说明一队.

public boolean isValid(String s) {
if(s.isEmpty()){
return true;
}
Stack<Character> stack=new Stack();
char[]t =s.toCharArray();
if(t.length%2!=0){
return false;
}
for(char c:t){
if(c=='('){
stack.push(')');
}else if(c=='['){
stack.push(']');
}else if(c=='{'){
stack.push('}');
}else if(stack.isEmpty()|| c !=stack.pop()){
return false;
}
}
return stack.isEmpty();
}
第二种解法
有点类似不过放入缓存中,去缓存中取
public boolean isValid(String s) {
if(s.isEmpty()){
return false;
}
char[]c=s.toCharArray();
if(c.length%2!=0){
return false;
}
Map<Character,Character>cache=new HashMap();
cache.put('}','{');
cache.put(')','(');
cache.put(']','[');
Stack<Character>stack=new Stack();
for(char cr:c){
if(cr=='('||cr=='['||cr=='{'){
//如果是左括号压入栈中
stack.push(cr);
}else if(stack.isEmpty()||cache.get(cr)!=stack.pop()){
return false;
}
}
return stack.isEmpty();
}
亚马逊,字节跳动,腾讯最近面试题,155. 最小栈
https://leetcode-cn.com/problems/min-stack/

使用辅助栈的方式,持有两个栈,一个是正常的一个是持有最小的栈,就是要排出一个问题,当正常栈中最小的弹出时,最小栈中也需要弹出,如果值一样的话也需要塞进去,这样就避免弹出后值不一样的情况.
private Stack<Integer>mStack;
private Stack<Integer>usuallyStack;
/** initialize your data structure here. */
public MinStack() {
mStack=new Stack();
usuallyStack=new Stack();
}
public void push(int x) {
if(mStack.isEmpty() || mStack.peek()>=x){
mStack.push(x);
}
usuallyStack.push(x);
}
public void pop() {
int top= usuallyStack.pop();
if(mStack.peek()==top){
mStack.pop();
}
}
public int top() {
return usuallyStack.peek();
}
public int getMin() {
return mStack.peek();
}
还有一种方式,我觉得更好的,少用一个辅助栈,但多占用栈的位置
min先取最大值,这样第一次放值的时候肯定能放进去了,如果放入的值更小于等于min,那需要先放原来数字,再赋值给最小值,然后再把最小值压入.
出栈的时候把栈顶元素送出即可,如果是最小值,需要把栈顶后面一个元素也出去,并赋值给min.

private int min=Integer.MAX_VALUE;
private Stack<Integer>stack;
/** initialize your data structure here. */
public MinStack() {
stack=new Stack();
}
public void push(int x) {
if(x<=min){
stack.push(min);
min=x;
}
stack.push(x);
}
public void pop() {
int top=stack.pop();
if(top==min){
min=stack.pop();
}
}
public int top() {
return stack.peek();
}
public int getMin() {
return min;
}
队列
存储结构及特点
队列(Queue)和栈一样,代表具有某一类操作特征的数据结构,我们拿日常生活中的一个场景来举例说明,我们去车站的窗口买票,那就要排队,那先来的人就先买,后到的人就后买,先来的人排到队头,后来的人排在队尾,不允许插队,先进先出,这就是典型的队列。
队列先进先出的特点英文表示为:First In First Out即FIFO,
为了更好的理解队列这种数据结构,我们以一幅图的形式来表示,并且我们将队列的特点和栈进行比较,如下:
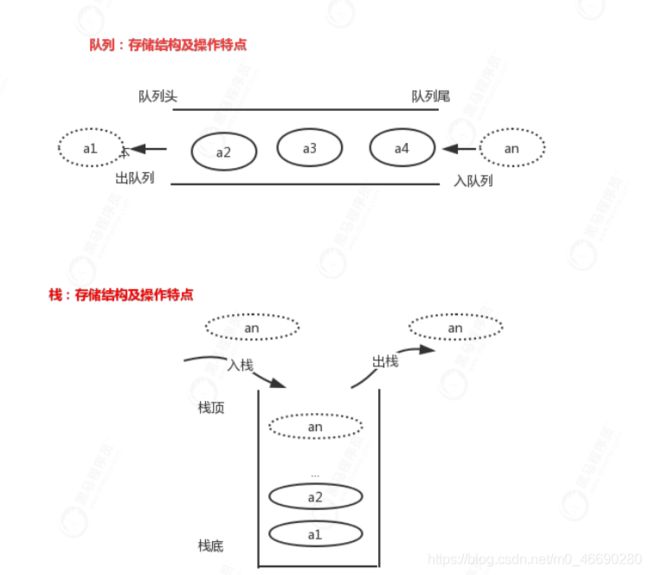
队列和栈一样都属于一种操作受限的线性表,栈只允许在一端进行操作,分别是入栈和出栈,而队列跟栈很相似,支持的操作也有限,最基本的两个操作一个叫入队列,将数据插入到队列尾部,另一个叫出队,从队列头部取出一个数据。
注意:入队列和出队列操作的时间复杂度均为O(1)
队列的实现
java API
像队列和栈这种数据结构在高级语言中的实现特别的丰富,也特别的成熟
Interface Queue:
Interface Deque:https://docs.oracle.com/javase/8/docs/api/java/util/Deque.html
在两端支持元素插入和移除的一种线性集合,这个接口定义了访问deque两端元素的方法

Class PriorityQueue:https://docs.oracle.com/javase/8/docs/api/java/util/PriorityQueue.html
元素不再遵循先进先出的特性了,出队列的顺序跟入队列的顺序无关,只跟元素的优先级有关系。队列中的每个元素都会指定一个优先级,根据优先级的大小关系出队列。插入操作是O(1)的复杂度,而取出操作是O(log n)的复杂度。
PriorityQueue底层具体实现的数据结构较为多样和复杂度:heap,BST等
基于链表实现队列
跟栈一样,队列可以用数组来实现,也可以用链表来实现。用数组实现的栈叫作顺序栈,用链表实现的栈叫作链式栈。同样,用数组实现的队列叫作顺序队列,用链表实现的队列叫作链式队列。
这一节我们来看基于单链表实现的队列,我们同样需要两个指针:head 指针和 tail 指针。它们分别指向链表的第一个结点和最后一个结点。如图所示,入队时,tail->next= new_node, tail = tail->next;出队时,head=head->next,如下图所示:
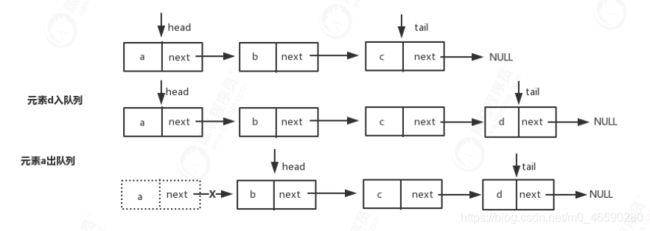
(1)创建队列接口Queue
public interface Queue<E> {
/**
* 返回队列中元素个数
* @return
*/
int size();
/**
* 判断队列是否为空
* @return
*/
boolean isEmpty();
/**
* 在不违反容量限制的情况下立即将指定的元素插入此队列,成功时返回true,
* 如果当前没有可用空间,则抛出IllegalStateException异常
* @param e
* @return
*/
boolean add(E e);
/**
* 在不违反容量限制的情况下立即将指定的元素插入到此队列中。成功时返回true,
* @param e
* @return
*/
boolean offer(E e);
/**
* 检索并删除此队列的头。如果队列为空抛出NoSuchElementException
* @return
*/
E remove();
/**
* 检索并删除此队列的头,如果此队列为空,则返回null。
* @return
*/
E poll();
/**
* 检索但不删除此队列的头。如果队列为空抛出NoSuchElementException
* 此方法与peek的不同之处在于,如果该队列为空,则会抛出异常。
* @return
*/
E element();
/**
* 检索但不删除此队列的头,或如果此队列为空,则返回null。
* @return
*/
E peek();
}
实现类
private static class Node<E>{
E val;
Node<E>next;
public Node(E val,Node<E>next){
this.val=val;
this.next=next;
}
}
//基于链表实现的
int size;
Node<E>head;
Node<E>tail;
@Override
public boolean add(Object e) {
linkLast(e);
return true;
}
private void linkLast(Object e){
Node<E>temp=tail;
Node<E> newNode = new Node<E>((E) e, null);
tail=newNode;
if (temp==null){
head=newNode;
}else {
temp.next=newNode;
}
}
@Override
public boolean offer(Object o) {
linkLast(o);
return true;
}
@Override
public Object remove() {
if (size==0){
}
Node<E> unlink = unlink();
return unlink.val;
}
private Node<E> unlink(){
Node<E>temp=head;
head=temp.next;
temp.next=null;
size--;
return temp;
}
@Override
public Object poll() {
if (size==0){
}
Node<E> unlink = unlink();
return unlink.val;
}
@Override
public Object element() {
return head.val;
}
@Override
public Object peek() {
return head.val;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size==0;
}
public String toString() {
StringBuilder sb = new StringBuilder();
Node<E> h = head;
while (h!=null){
sb.append(h.val).append("->");
h = h.next;
}
return sb.append("null").toString();
}
测试代码
public static void main(String[] args) {
Queue queue = new LinkedListQueue();
queue.add("1");
queue.offer("2");
queue.offer("3");
queue.offer("4");
System.out.println("队列是否为空:"+queue.isEmpty()+",队列元素个数为:"+queue.size());
System.out.println(queue);
System.out.println("队列头元素:"+queue.remove());
System.out.println(queue);
System.out.println("队列头元素:"+queue.poll());
System.out.println(queue);
System.out.println("队列头元素:"+queue.element());
System.out.println(queue);
System.out.println("队列头元素:"+queue.peek());
System.out.println(queue);
}
基于数组实现队列
public class ArrayQueue {
// 存储数据的数组
private Object[] elements;
//队列大小
private int size;
// 默认队列容量
private int DEFAULT_CAPACITY = 10;
// 队列头指针
private int head;
// 队列尾指针
private int tail;
private int MAX_ARRAY_SIZE = Integer.MAX_VALUE-8;
/**
* 默认构造函数 初始化大小为10的队列
*/
public ArrayQueue(){
elements = new Object[DEFAULT_CAPACITY];
initPointer(0,0);
}
/**
* 通过传入的容量大小创建队列
* @param capacity
*/
public ArrayQueue(int capacity){
elements = new Object[capacity];
initPointer(0,0);
}
/**
* 初始化队列头尾指针
* @param head
* @param tail
*/
private void initPointer(int head,int tail){
this.head = head;
this.tail = tail;
}
/**
* 元素入队列
* @param element
* @return
*/
public boolean offer(Object element){
ensureCapacityHelper();
elements[tail++] = element;//在尾指针处存入元素且尾指针后移
size++;//队列元素个数加1
return true;
}
private void ensureCapacityHelper() {
if(tail==elements.length){
//尾指针已越过数组尾端
//判断队列是否已满 即判断数组中是否还有可用存储空间
//if(size
if(head==0){
//扩容
grow(elements.length);
}else{
//进行数据搬移操作 将数组中的数据依次向前挪动直至顶部
for(int i= head;i<tail;i++){
elements[i-head]=elements[i];
}
//数据搬移完后重新初始化头尾指针
initPointer(0,tail-head);
}
}
}
/**
* 扩容
* @param oldCapacity 原始容量
*/
private void grow(int oldCapacity) {
int newCapacity = oldCapacity+(oldCapacity>>1);
if(newCapacity-oldCapacity<0){
newCapacity = DEFAULT_CAPACITY;
}
if(newCapacity-MAX_ARRAY_SIZE>0){
newCapacity = hugeCapacity(newCapacity);
}
elements = Arrays.copyOf(elements,newCapacity);
}
private int hugeCapacity(int newCapacity) {
return (newCapacity>MAX_ARRAY_SIZE)? Integer.MAX_VALUE:newCapacity;
}
/**
* 出队列
* @return
*/
public Object poll(){
if(head==tail){
return null;//队列中没有数据
}
Object obj=elements[head++];//取出队列头的元素且头指针后移
size--;//队列中元素个数减1
return obj;
}
/**
* 获取队列元素个数
* @return
*/
public int size() {
return size;
}
/**
* 判断队列是否为空
* @return
*/
public boolean isEmpty() {
return size==0;
}
}
测试类
public static void main(String[] args) {
ArrayQueue queue = new ArrayQueue(4);
//入队列
queue.offer("itcast1");
queue.offer("itcast2");
queue.offer("itcast3");
queue.offer("itcast4");
//此时入队列应该走扩容的逻辑
queue.offer("itcast5");
queue.offer("itcast6");
//出队列
System.out.println(queue.poll());
System.out.println(queue.poll());
//此时入队列应该走数据搬移逻辑
queue.offer("itcast7");
//出队列
System.out.println(queue.poll());
//入队列
queue.offer("itcast8");
//出队列
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
System.out.println(queue.poll());
//入队列
queue.offer("itcat9");
queue.offer("itcat10");
queue.offer("itcat11");
queue.offer("itcat12");
//出队列
System.out.println(queue.poll());
System.out.println(queue.poll());
}
小结
- 队列的实现如果基于数组,其实就是操作下标,我们维护两个下标,head,tail分别代表队列的头,尾指针,如图:
删除的时候头向后移动,所以判断满不满还需要看头是不是0的位置,不是的话数据依次向前移动

- 当然,在java中有一个比较常用的实现:java.util.LinkedList,我们先来看它的定义
public class LinkedList<E>
extends AbstractSequentialList<E>
implements List<E>, Deque<E>, Cloneable, java.io.Serializable
LinkedList实现了List,Deque接口,而Deque又继承自Queue接口
public interface Deque<E> extends Queue<E>
https://docs.oracle.com/javase/8/docs/api/java/util/Deque.html
从Deque接口的定义可以看出,它里面不仅包含队列操作的相关api,比如add,offer,peek,poll等,还有双端队列操作的api,如addFirst,offerFirst,peekFirst等等。除此之外它还包含栈相关的操作api,如push,pop。
也就是说LinkedList功能是多样性的,能当作List集合用,能当作Queue队列用,能当作Deque双端队列用,也能当作Stack栈来使用。
实战
622. 设计循环队列
https://leetcode-cn.com/problems/design-circular-queue/

循环队列很重要的一个作用是复用之前使用过的内存空间,适合用数组实现,使用链表的实现,创建结点和删除结点都是动态的,也就不存在需要循环利用的问题了。而且用数组实现循环队列也不要求我们对数组进行动态扩容与缩容。
思路分析:
循环队列,顾名思义,它长得像一个环。原本数组是有头有尾的,是一条直线。现在我们把首尾相连,形成了一个环,如下图所示:

从图中可知队列的大小为11,当前 head=1,tail=10。队列中9个元素,当有一个新的元素 a(10) 入队时,我们放入下标为10的位置。但这个时候,我们并不把 tail 更新为11,而是将其在环中后移一位,到下标为 0 的位置。所以,在 a(10)入队之后,循环队列中的元素就变成了下面的样子:

通过这样的方法,我们成功避免了数据搬移操作,也能重复利用已有的内存空间,看起来不难理解,但是循环队列的代码最关键的是如何确定好队空和队满的判定条件。
那如何来判定循环队列为空或者已满呢?
看到上面的图很多人立马想到说如果再向循环队列中存一个元素a(11),将a(11)存入下标为0的位置,然后尾指针加1变成1,此时head=1,tail=1,所以立马决断出当满足head=tail时循环队列已满,这个结果真的对吗?
那我们在转换分析一下什么情况下队列为空?
注意我们现在说的都是基于数组的循环队列,对比我们之前非循环的顺序队列判断为空的条件来看,如果是循环队列为空的条件仍然是head=tail,那此时就有冲突了,当head=tail时到底是队列为空还是队列已满?因此我们关于队列已满的判断条件并不正确,我们也不认为当把元素a(11)存入之后队列就满了,反而我们认为上面图中所画情况就是队列已满的情况,如果你还是不甚明白,我们再接着画几个队列已满的情况

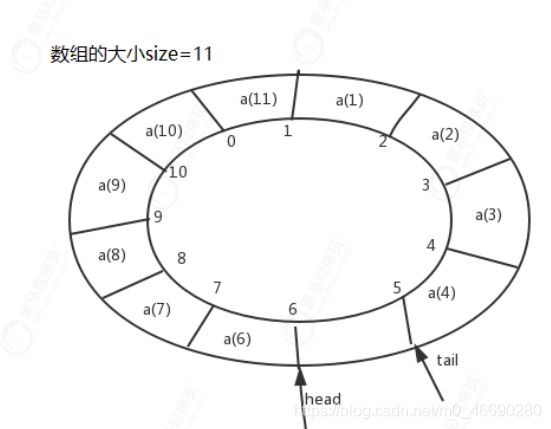
我们把这种情况下的循环队列称之为队列已满,我们发现当队列满时,图中的 tail 指向的位置实际上是没有存储数据的,所以:
为了避免“队列为空”和“队列为满”的判别条件冲突,我们有意浪费了一个位置。
判别队列为空的条件是:head== tail;;
判别队列为满的条件是:(tail+ 1) % capacity == head;。可以这样理解,当 tail 循环到数组的前面,要从后面追上 front,还差一格的时候,判定队列为满,其中capacity 为数组的大小
int size;
int[]elementData;
int front;
int rear;
/** Initialize your data structure here. Set the size of the queue to be k. */
public MyCircularQueue(int k) {
this.size=k+1;
elementData=new int[k+1];
front=rear=0;
}
/** Insert an element into the circular queue. Return true if the operation is successful. */
public boolean enQueue(int value) {
if(isFull()){
return false;
}
elementData[rear]=value;
rear=(rear+1)%size;
return true;
}
/** Delete an element from the circular queue. Return true if the operation is successful. */
public boolean deQueue() {
if(isEmpty()){
return false;
}
front=(front+1)%size;
return true;
}
/** Get the front item from the queue. */
public int Front() {
if(isEmpty()){
return -1;
}
return elementData[front];
}
/** Get the last item from the queue. */
public int Rear() {
if(isEmpty()){
return -1;
}
int index=(rear-1+size)%size;
return elementData[index];
}
/** Checks whether the circular queue is empty or not. */
public boolean isEmpty() {
return front==rear;
}
/** Checks whether the circular queue is full or not. */
public boolean isFull() {
return front==(rear+1)%size;
}
641. 设计循环双端队列
https://leetcode-cn.com/problems/design-circular-deque/

和上面一样的,就几个细节讲一下,多放一个值来判断是否已满,所以存入的时候size+1,因为是循环的关系,所以加移动的时候需要+1并且除以size来确定位置,
int size;
int front;
int rear;
int[] elementData;
/** Initialize your data structure here. Set the size of the queue to be k. */
public MyCircularQueue(int k) {
this.size=k+1;
elementData=new int[k+1];
rear=front=0;
}
/** Insert an element into the circular queue. Return true if the operation is successful. */
public boolean enQueue(int value) {
if(isFull()){
return false;
}
elementData[rear]=value;
rear=(rear+1)%size;
return true;
}
/** Delete an element from the circular queue. Return true if the operation is successful. */
public boolean deQueue() {
if(isEmpty()){
return false;
}
front=(front+1)%size;
return true;
}
/** Get the front item from the queue. */
public int Front() {
if(isEmpty()){
return -1;
}
return elementData[front];
}
/** Get the last item from the queue. */
public int Rear() {
if(isEmpty()){
return -1;
}
int index=(rear-1+size)%size;
return elementData[index];
}
/** Checks whether the circular queue is empty or not. */
public boolean isEmpty() {
return rear==front;
}
/** Checks whether the circular queue is full or not. */
public boolean isFull() {
return front==(rear+1)%size;
}
703. 数据流中的第K大元素
https://leetcode-cn.com/problems/kth-largest-element-in-a-stream/

这里采用优先级队列,按自然数大小排序,出栈的是最小的值.
设置k为栈中允许存放的最大数量,入栈的时候判断一下size满了吗,没有就塞,有了的话,判断一下栈中存放的最小值和要存入的值大小,如果入队列的值比栈中存放的最小值要小,那就不入队列,如果大那就把最小值弹出,把这个值入队列.
比如3,5,6,2,8,7 k=3
3.5.6入栈,2的时候不入,8,7入,3,5出,这样就变成了6,7,8这样6就是第三大的数了.
int k;
PriorityQueue<Integer> queue;
public KthLargest(int k, int[] nums) {
this.k=k;
queue=new PriorityQueue(k);
for(int num:nums){
add(num);
}
}
public int add(int val) {
if(queue.size()<k){
queue.offer(val);
}else if(val>queue.peek()){
queue.poll();
queue.offer(val);
}
return queue.peek();
}
栈和队列面试题
腾讯,字节跳动最近面试题,232. 用栈实现队列
https://leetcode-cn.com/problems/implement-queue-using-stacks/

这里的实现方式是基于栈先进后出,队列先进先出的特点实现的.使用辅助栈,
创建两个栈,一个用来放数据,一个用来把前一个栈的数据放进去,这样就形成了两次的压栈,翻转,也就变成了先进先出的数据结构
class MyQueue {
Deque<Integer>left;
Deque<Integer>right;
/** Initialize your data structure here. */
public MyQueue() {
left=new ArrayDeque();
right=new ArrayDeque();
}
/** Push element x to the back of queue. */
public void push(int x) {
left.push(x);
}
private void reverse(){
if(right.isEmpty()){
while(!left.isEmpty()){
right.push(left.pop());
}
}
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
reverse();
return right.pop();
}
/** Get the front element. */
public int peek() {
reverse();
return right.peek();
}
/** Returns whether the queue is empty. */
public boolean empty() {
return left.isEmpty()&&right.isEmpty();
}
}
字节跳动,facebook最近面试题,225. 用队列实现栈
https://leetcode-cn.com/problems/implement-stack-using-queues/

队列:先进先出,栈:先进后出
队列先进一个元素,比如说1,当4进队列的时候,把1取出来,再进一次队列,这样就变成4,1的顺序,也就变成了栈先进后出…内部操作一下.

class MyStack {
Queue<Integer>queue;
/** Initialize your data structure here. */
public MyStack() {
queue=new LinkedList();
}
/** Push element x onto stack. */
public void push(int x) {
queue.add(x);
for(int i=1;i<queue.size();i++){
queue.add(queue.poll());
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.poll();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
华为,网易,腾讯最近面试题,84. 柱状图中最大的矩形(重点)
https://leetcode-cn.com/problems/largest-rectangle-in-histogram/

1.暴力解法

高度是当前索引的值大小,但宽这个需要往两边扩散,找到第一个小于当前索引值的就停下来,然后回退一格,比如说右3,左2,也就是两个数字了,3-2需要加1来得到宽.
public int largestRectangleArea(int[] heights) {
int max=0;
for( int i=0;i<heights.length;i++){
//用左右两个指针分别扩散,寻找为heights[i]为高度的最大矩形的左右两个下标
int left=i;
int right=i;
while(left>0){
left--; //向左移动
if(heights[left]<heights[i]){
left++;//先向前移动一格了,如果找到了回退一格;
break;
}
}
while(right<heights.length-1){
right++;
if(heights[right]<heights[i]){
right--;
break;
}
}
int tempArea=(right-left+1)*heights[i];
max=max>tempArea?max:tempArea;
}
return max;
}
2.单调栈+哨兵解决
单调栈,分为单调递增栈和单调递减栈,这里拿单调递减栈为例,刚开始栈为空,6压入,下一个元素10,大于6,压入,下一个3,发现10,6都比3小,都弹出,压入3,也就是栈底元素永远是最小的,栈顶到栈顶元素大小依次递减.
那这个单调栈有什么作用呢?以3压入栈的时候为例,需要把10,6弹栈,压入3.这个时候10是知道自己的左边是6的,也知道自己的右边是3了
再以4入栈为例,7知道自己的左边元素是3,当自己需要弹栈的那一刻,它知道自己的右边是4了,这样其实左右指针的位置就明确了.

实现一个单调递减栈
private int[]getLeftMinNum(int[]src){
int[]result=new int[src.length];
Deque<Integer> monotoneStack=new ArrayDeque<>();
for (int i=0;i<src.length;i++){
while (!monotoneStack.isEmpty()&&src[i]<=monotoneStack.peek()){
monotoneStack.pop();
}
if (!monotoneStack.isEmpty()){
result[i]=monotoneStack.peek();
}else {
result[i]=-1;
}
monotoneStack.push(src[i]);
}
return result;
}
public static void main(String[] args) {
int []param=new int[]{
6,10,3,7,4,4,12,5};
System.out.println(Arrays.toString(new getLeftMin().getLeftMinNum(param)));
}
时间复杂度:O(N)
空间复杂度:O(N)
哨兵
单调栈的优化,以上代码在编写的时候需要考虑如下情况
1、遇到入栈元素比栈顶元素小,则先需要栈顶元素出栈,一直到 入栈元素大于栈顶元素,弹出栈顶元素的时候要考虑栈为空的情况,因此while循环的条件中有一个 !monotoneStack.isEmpty()
2、以及最后当入栈元素大于了栈顶元素之后还需要判断栈不为空,则获取栈顶元素作为入栈元素左边第一个小于它的元素,否则取-1;我们需要判断栈是否为空!
解决方案:哨兵,事先在栈中存一个 -1 ,这样在循环入栈的整个过程中就不需要做栈空的判断了,改进后的代码其实在提前加入哨兵
monotoneStack.push(-1)
哨兵的作用就是:遇到哨兵就相当于栈空了!代表了一种边界情况,所以一般可以用哨兵来减少一些边界判断
public int largestRectangleArea(int[] heights) {
//特殊判断
if(heights==null){
return 0;
}
//构造一个新数组,安排哨兵
int[]h=new int[heights.length+2];
h[0]=-1;
h[h.length-1]=-1;
System.arraycopy(heights,0,h,1,heights.length);
Deque<Integer>stack=new ArrayDeque();
//遍历前将左侧哨兵入栈
stack.push(0);
//定义最大面积
int max=0;
for(int i=1;i<h.length;i++){
//比自己值小和等于的值都可以计算
while(h[i]<h[stack.peek()]){
//栈顶元素对应的高度
int height=h[stack.pop()];
max=Math.max(max,(i-1-stack.peek())*height);
}
stack.push(i);
}
return max;
}
字节跳动,华为,腾讯最近面试题,42. 接雨水
https://leetcode-cn.com/problems/trapping-rain-water/

这里采用单调递增栈来实现,
public int trap(int[] height) {
if(height==null){
return 0;
}
//构造单调栈,此处两边需要哨兵,原因是因为两侧肯定是装不了水的,如果加入了哨兵要么就让两侧能装 水了,要么就是导致中间的计算结果不正确
Deque<Integer>stack=new ArrayDeque();
int max=0;
for(int i=0;i<height.length;i++){
while(!stack.isEmpty()&&height[i]>=height[stack.peek()]){
int p=stack.pop();
if(!stack.isEmpty()){
max += (Math.min(height[stack.peek()], height[i]) - height[p]) * (i- stack.peek()-1);
}
}
stack.push(i);
}
return max;
}
字节跳动,谷歌,亚马逊最近面试题,239. 滑动窗口最大值
https://leetcode-cn.com/problems/sliding-window-maximum/

1.暴力解法,但官方不认可AC(通过)
思路:拿到k的最后一个值,定一个临时变量,然后往前遍历比较每个值,把组最大放进去,最后把最大值拿到返回
k-1是取第一个框的最后一个索引值,然后j是从后往前遍历,取最大值.
public int[] maxSlidingWindow(int[] nums, int k) {
//特殊判断
if(nums==null){
return new int[]{
};
}
//定义结果数组
List<Integer>list=new ArrayList();
for(int i=k-1;i<nums.length;i++){
int max=nums[i];
//窗口内比较值,往前遍历
for(int j=i;j>i-k;j--){
max=Math.max(max,nums[j]);
}
list.add(max);
}
int[] result = list.stream().mapToInt(Integer::valueOf).toArray();
return result;
}
2、单调队列
同单调栈,单调队列也分单调递增队列(队头到队尾递增,队列头是最小元素),单调递减队列(队头到队尾
递减,队列头是最大元素),一般用来解决滑动窗口内的最值问题
创建一个单调递减队列,也就是头元素是最大的,尾最小.
比如1,3,4,5,6,3,2 入队列,1进,3的时候1先出3再进,4的时候3先出4再进,这样的顺序,到下一个3的时候,入队列,也就是存6,3,2最后,每一次i拿的时候是当前队列下标的元素,
public int[] maxSlidingWindow(int[] nums, int k) {
//特殊判断
if(nums==null||nums.length<k){
return new int[]{
};
}
//存储结果集
int[]result=new int[nums.length-k+1];
int r=0;
//利用单调递减队列,队列中存储元素下标
Deque<Integer>queue=new LinkedList();
for(int i=0;i<nums.length;i++){
//如果入队列的值要
while(!queue.isEmpty()&&nums[i]>nums[queue.peekLast()]){
queue.pollLast();
}
queue.offerLast(i);
if(i>=k-1){
//保证后面获取的最大值是在滑动窗口内,只需要用当前下标-队列头(最大值)如果超过窗口大小则将队列头出队列
if(i-queue.peekFirst()>=k){
queue.pollFirst();
}
result[r++]=nums[queue.peekFirst()];
}
}
return result;
}


