【建议收藏】数据结构和算法面试题
数据结构
数据结构分为两大类,线性结构和非线性结构。
- 线性结构:数组、队列、链表、栈
- 非线性结构:多维数组、树结构、图结构
1.数组
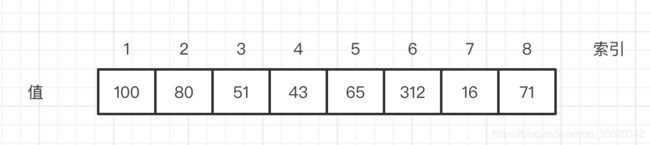
数组是最常用的数据结构,用于存储相同类型的数据,数组的长度也是固定的。
数组是有序的,存储是按照先后顺序进行的,数组中的元素存储在一个连续性的内存块中,我们可以通过value和索引进行数据的访问和更新。如图所示:
优点:
①通过下标方式访问元素,速度快,时间复杂度o(1)。
②对于有序数组,还可以使用二分查找提高检索速度
缺点:
①插入、删除操作效率较低
②如果要检索具体某一个值,需要遍历所有效率较低。
时间复杂度:
查询:o(1)
插入:o(n)
删除:o(n)
2.链表
链表是以节点的方式来存储,每个节点包含数据和next指针。
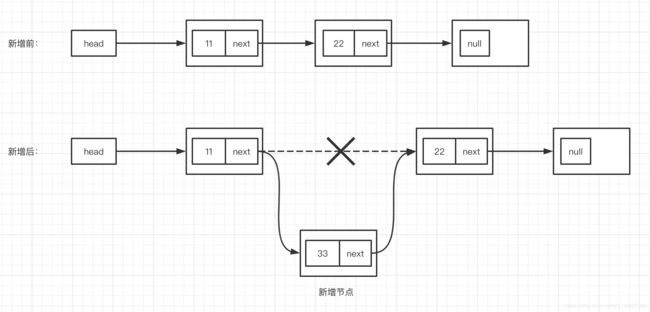
单向链表
插入:找到要插入的位置,把前面一个元素next指向新节点,新节点把next指向后面一个元素
删除:把前面一个元素的next指向后面一个元素
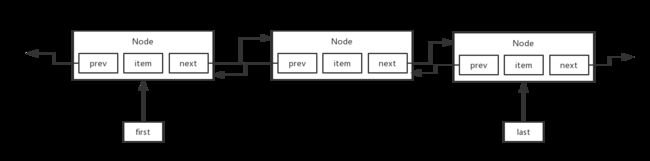
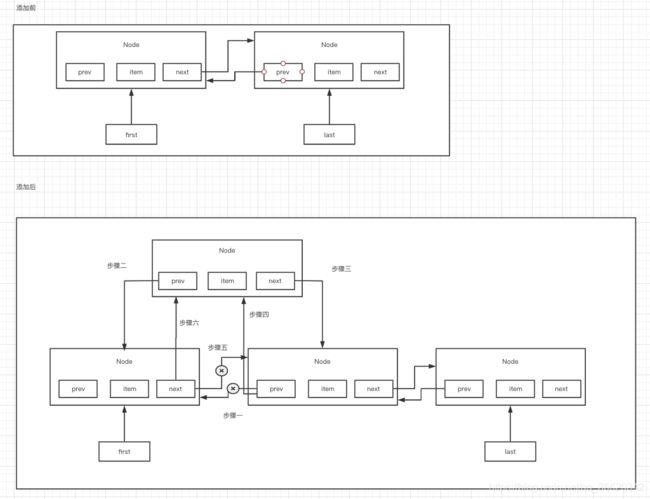
双向链表
item是元素,prev、next是指针
插入元素的原理
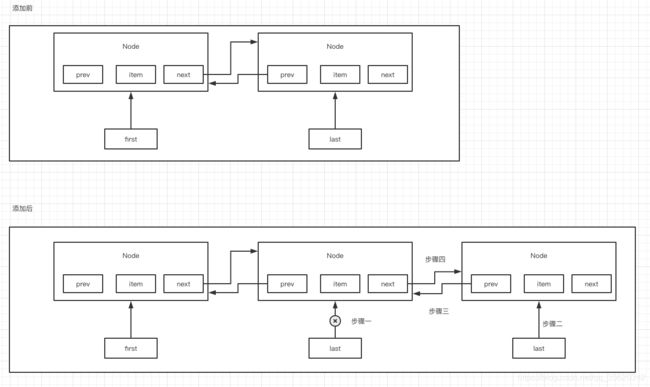
(1)尾部插入
add(),默认就是在队列的尾部插入一个元素,在那个双向链表的尾部插入一个元素
addLast(),跟add()方法是一样的,也是在尾部插入一个元素
public boolean add(E e) {
linkLast(e);
return true;
}
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
(2)队列中间插入
add(index, element),是在队列的中间插入一个元素
public void add(int index, E element) {
checkPositionIndex(index);
if (index == size)
linkLast(element);
else
linkBefore(element, node(index));
}
void linkBefore(E e, Node<E> succ) {
// assert succ != null;
final Node<E> pred = succ.prev;
final Node<E> newNode = new Node<>(pred, e, succ);
succ.prev = newNode;
if (pred == null)
first = newNode;
else
pred.next = newNode;
size++;
modCount++;
}
Node<E> node(int index) {
// assert isElementIndex(index);
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
(3)头部插入
addFirst(),在队列的头部插入一个元素
public void addFirst(E e) {
linkFirst(e);
}
private void linkFirst(E e) {
final Node<E> f = first;
final Node<E> newNode = new Node<>(null, e, f);
first = newNode;
if (f == null)
last = newNode;
else
f.prev = newNode;
size++;
modCount++;
}
获取元素的原理
(1)获取头部元素
getFirst() 获取头部的元素,他其实就是直接返回first指针指向的那个Node他里面的数据,他们都是返回头部的元素。getFirst()如果是对空list调用,会抛异常;peek()对空list调用,会返回null
(2)获取尾部元素
getLast():获取尾部的元素,他其实就是直接返回last指针指向的那个Node他里面的数据
public E getLast() {
final Node<E> l = last;
if (l == null)
throw new NoSuchElementException();
return l.item;
}
(3)获取中间的元素
public E get(int index) {
checkElementIndex(index);
return node(index).item;
}
Node<E> node(int index) {
// assert isElementIndex(index);
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
对于双向链表而言,get(int index)这个方法,是他的弱项,也是他的缺点,如果他要获取某个随机位置的元素,需要使用node(index)这个方法,是要进行链表的遍历,会判断一下index和size >> 1进行比较,如果在前半部分,就会从头部开始遍历;如果在后半部分,就会从尾部开始遍历
删除元素的原理
(1)删除尾部
(2)删除头部
(3)删除中间的元素
新增和删除差不多,理解了新增,删除就so easy了,在这里我就不详细说明了。
链表的优缺点:
优点:插入、删除效率较高,时间复杂度o(1)
缺点:查询较慢,时间复杂度为o(n)
3.栈
栈stack:先入后出FILO(first in last out)
Push 推送:在堆栈顶部插入一个元素。
Pop 弹出:删除最上面的元素并返回。
用队列实现栈,LeetCode链接:https://leetcode-cn.com/problems/implement-stack-using-queues/solution/yong-dui-lie-shi-xian-zhan-by-leetcode-solution/
LeetCode里有动态过程图,在这里我就不画了,大家可以点开链接查看。
数组实现栈
public class ArrayStack {
private int maxSize;// 最大的尺寸
private int[] stack;// 使用数组模拟
private int top = -1;// 栈指针 , 初始为-1
public ArrayStack(int maxSize) {
// 初始化
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 判断是否为空
public boolean isEmpty(){
return top == -1;
}
// 判断是否为满
public boolean isFull(){
return top == maxSize - 1;
}
// 进栈
public void push(int value){
// 判断满栈
if(isFull()){
System.out.println("栈满~~");
return;
}
top++;
stack[top] = value;
}
// 出栈 -- 从栈顶出栈
public int pop(){
if(top == -1){
throw new RuntimeException("栈空~~");
}
int value = stack[top];
top--;
return value;
}
// 遍历栈 == 从栈顶开始遍历
public void stackList(){
if(isEmpty()){
throw new RuntimeException("栈空~~");
}
for (int i = 0; i < maxSize ; i++) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
}
public static void main(String[] args) {
// 初始化栈
ArrayStack arrayStack = new ArrayStack(5);
// 入栈
arrayStack.push(1);
arrayStack.push(2);
arrayStack.push(5);
arrayStack.push(8);
arrayStack.push(6);
// 遍历
arrayStack.stackList();
// 出栈
int value1 = arrayStack.pop();
System.out.println(value1);
}
链表实现栈
/**
* 用单链表实现栈
* 表示链表的一个节点
*/
public class Node {
Object element;
Node next;
public Node(Object element){
this(element,null);
}
/**
* 创建一个新的节点
* 让他的next指向,参数中的节点
* @param element
* @param n
*/
public Node(Object element,Node n){
this.element=element;
next=n;
}
public Object getElement() {
return element;
}
}
public class ListStack {
Node header;//栈顶元素
int elementCount;//栈内元素个数
int size;//栈的大小
/**
* 构造函数,构造一个空的栈
*/
public ListStack(){
header=null;
elementCount=0;
size=0;
}
/**
* 通过构造器自定义栈的大小
* @param size
*/
public ListStack(int size) {
header=null;
elementCount=0;
this.size=size;
}
public void setHeader(Node header) {
this.header=header;
}
public boolean isFull() {
if (elementCount==size) {
return true;
}
return false;
}
public boolean isEmpty() {
if (elementCount==0) {
return true;
}
return false;
}
/**
* 入栈
* @param value
*/
public void push(Object value) {
if (this.isFull()) {
throw new RuntimeException("Stack is Full");
}
//注意这里面试将原来的header作为参数传入,然后以新new出来的Node作为header
header=new Node(value, header);
elementCount++;
}
/**
* 出栈
* @return
*/
public Object pop() {
if (this.isEmpty()) {
throw new RuntimeException("Stack is empty");
}
Object object=header.getElement();
header=header.next;
elementCount--;
return object;
}
/**
* 返回栈顶元素
*/
public Object peak(){
if (this.isEmpty()) {
throw new RuntimeException("Stack is empty");
}
return header.getElement();
}
}
时间复杂度:
查找:o(n)
插入:o(1)
删除:o(1)
栈的应用场景:
- 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。(学过JVM的同学是不是很熟悉)
- 处理递归调用:和子程序的调用类似,只是除了存储下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
4.队列
队列queue:先入先出FIFO(first in first out)
用栈实现队列,LeetCode链接:https://leetcode-cn.com/problems/implement-queue-using-stacks/solution/yong-zhan-shi-xian-dui-lie-by-leetcode/
用数组和链表实现队列,LeetCode链接:https://leetcode-cn.com/problems/design-circular-queue/solution/she-ji-xun-huan-dui-lie-by-leetcode/
具体思路和代码可以在LeetCode上查看,写的挺好的,而且有动态的过程图,我这里就不重复阐述了。
时间复杂度:
查找:o(n)
插入:o(1)
删除:o(1)
5.二叉树
这里我给大家推荐一个非常棒的网站https://www.cs.usfca.edu/~galles/visualization/Algorithms.html,他可以看所有数据结构的演变过程,对于数据结构学习来说,非常重要。
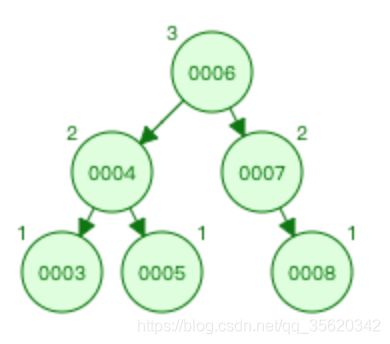
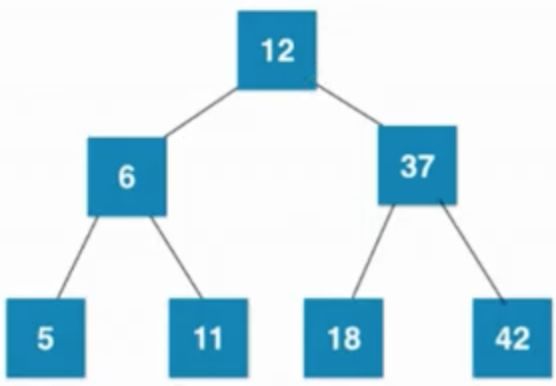
二叉树:二叉树是每个节点最多有两个子树的树结构。
根节点:一棵树最上面的节点称为根节点。
父节点、子节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子节点,例如23是13的父节点,13是10的父节点,13和54都是23的子节点。
叶子节点:没有任何子节点的节点称为叶子节点。例如10、30、28、77都是叶子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点。 例如13和54都是23的子节点,那么13和54就是兄弟节点。
节点度:就是节点下子树个树。上图中,13的度为2,46的度为1,28的度为0。
节点的权:节点的值
树的深度:从根节点开始(其深度为0)自顶向下逐层累加的。上图中,13的深度是1,30的深度是2,28的深度是3。
树的高度:从叶子节点开始(其高度为0)自底向上逐层累加的。54的高度是2,根节点23的高度是3。
对于树中相同深度的每个节点来说,它们的高度不一定相同,这取决于每个节点下面的叶子节点的深度。上图中,13和54的深度都是1,但是13的高度是1,54的高度是2。
6.二叉搜索树
左子树上所有节点的值均小于它的根节点的值
右子树上所有节点的值均大于它的根节点的值
二叉搜索树:判断二叉树是否是搜索树,满足左子树上所有节点的值均小于它的根节点的值且右子树上所有节点的值均大于它的根节点的值,满足这两个条件的二叉树就是二叉搜索树。
时间复杂度o(log(n))
遍历:
前序:23、13、10、30、54、46、28、77,(根、左、右),先输出父节点,再遍历左子树,再遍历右子树
中序:10、13、30、23、28、46、54、77,(左、根、右),先遍历左子树,再输出父节点,再遍历右子树
后序:10、30、13、28、46、77、54、23,(左、右、根),先遍历左子树,再遍历右子树,最后输出父节点
总结:看输出父亲节点的顺序,就可以确定是前序、中序、后序
优点:
①它的检索效率较高,类似于二分查找。
②它的增删改效率较高,因为它使用的是指针的方式,不会导致整个结构的移动。
缺点:
假如说没有左子树只有右子树,每次都只有右子树,之后就会变成一个链表,之后时间复杂度会退化成o(n)
7.二叉平衡树
假如说没有左子树只有右子树,每次都只有右子树,之后就会变成一个链表,之后时间复杂度会退化成o(n),此时平衡二叉树应运而生。
平衡二叉树也叫平衡二叉搜索树,又被称为AVL树。
补充:AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis
特点:
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,平衡二叉树的常用实现方法有红黑树、AVL(算法)、替罪羊树、Treap、伸展树。
当左子树高度-右子树高度>1,向右旋转,目的是降低左子树高度。
当右子树高度-左子树高度>1,向左旋转,目的是降低右子树高度。
8.平衡二叉树之2-3树
2-3树是最简单的B树结构,其特点如下:
①所有的叶子节点都在同一层(只要是B树都满足这一条件)
补充:添加节点永远不会添加到一个为空的位置,插入一个新节点,小于根节点插入到根节点左子树,若左子树为空,则新节点融合到根节点左边
②有两个子节点的节点叫做二节点,二节点要么没有子节点,要么有两个子节点
③有三个子节点的节点叫做三节点,三节点要么没有子节点,要么有三个子节点
④2-3树由二节点和三节点构成的树,2就代表二节点,3就代表三节点
补充:2-3树满足二分搜索树的基本性质
2-3名字由来:每个节点有2个或者3个孩子,所以叫2-3树
27就是二节点,8、12是三节点
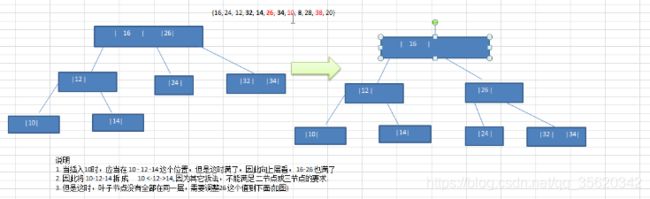
2-3树是一棵绝对平衡的树,从根节点到任意一个叶子节点,经过的节点数量是相同的
2-3树是如何维持绝对的平衡?
1)加入节点:
1.1)二叉搜索树:
插入一个新节点,小于根节点插入到根节点左子树,若左子树为空,则直接成为根节点的左孩子节点
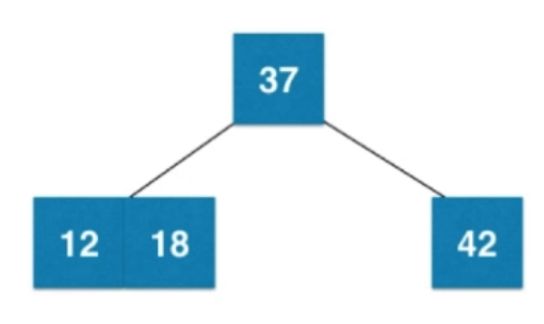
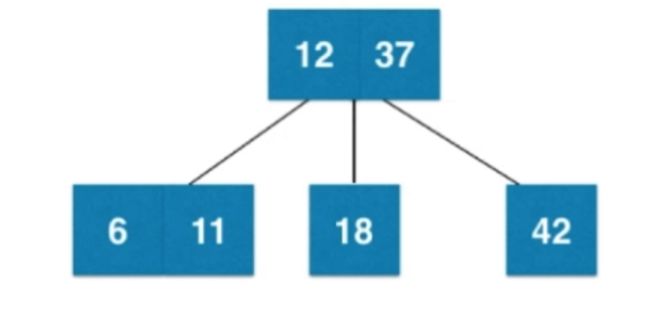
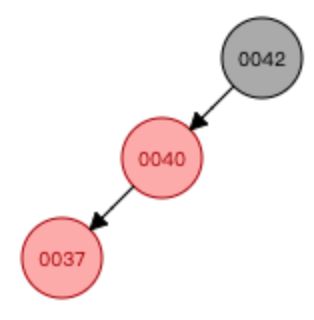
插入数字:42、37、12
解释:添加节点永远不会添加到一个为空的位置,插入一个新节点,小于根节点插入到根节点左子树,若左子树为空,则新节点融合到根节点左边
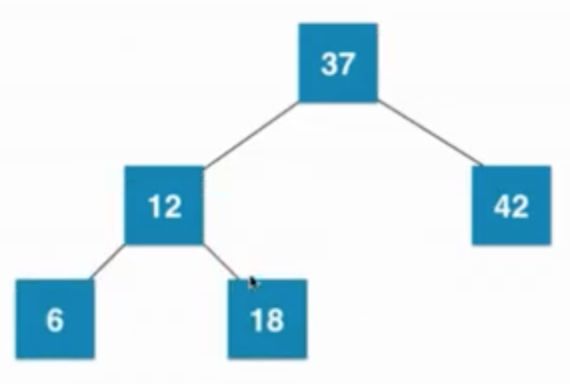
②插入数字12
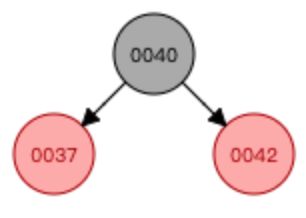
同上,37的左子树为空,则新节点融合到根节点左边,然后形成临时的4节点,(当节点有三个元素,就可以有4个孩子,但是2-3树,最多只能有3个孩子,因此需要分裂),之后会进行分裂,如下图所示:
由 分裂成
分裂成
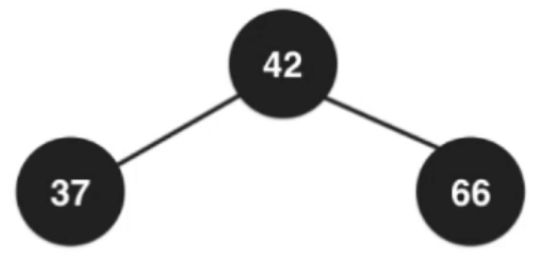
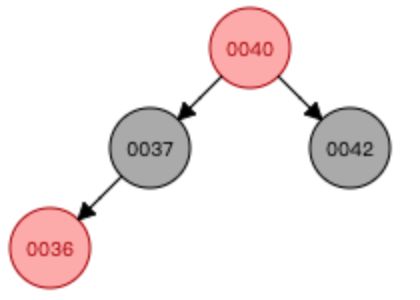
④插入数字6
当叶子节点已经是3节点(12、18),父亲节点是2节点(37),之后暂时融合成一个临时4节点,然后再拆分,然后子树新的根节点是12,12需要向上和父亲节点融合
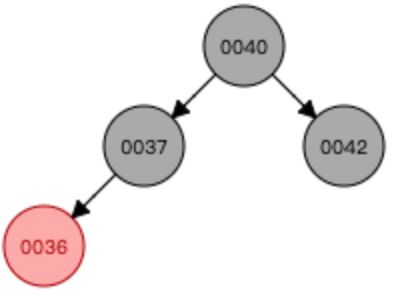
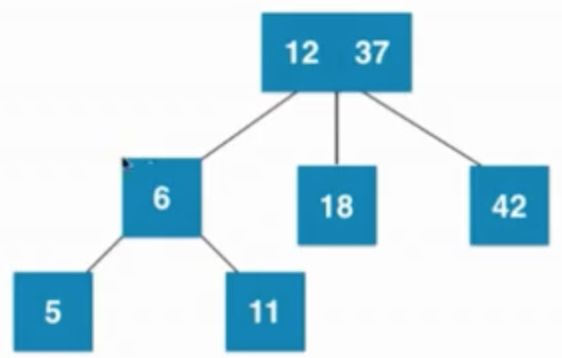
⑥插入数字5
当叶子节点已经是3节点(6、11),父亲节点是3节点(12、37),之后暂时融合成4节点,然后再拆分,然后子树新的根节点是6,6需要向上和父亲节点融合,然后暂时融合成一个临时4节点,之后在拆分成3个2节点组成的子树
由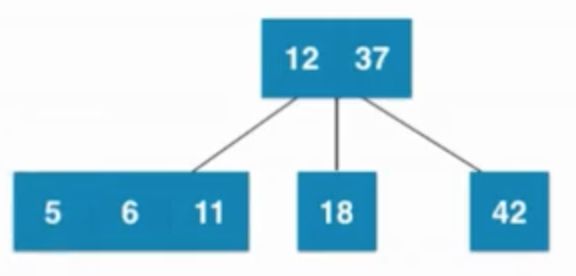 —>
—> —>
—>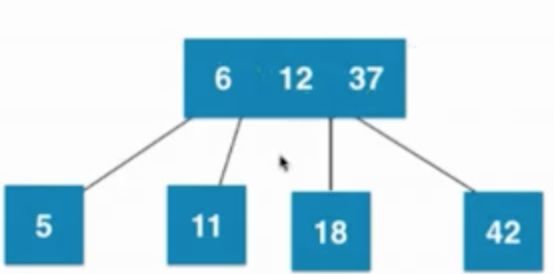 —>
—>
9.红黑树
红黑树特性:
①每个节点或者是红色的,或者是黑色的
②根节点是黑色的
③每一个叶子节点(最后的空节点)是黑色的
④如果一个节点是红色的,那么他的孩子节点都是黑色的
⑤从任意一个节点到叶子节点,经过的黑色节点是一样的
补充:所有的红色节点是左倾斜的
案例1:颜色翻转
②添加数字37
黑色节点左右子树为空,直接把37添加进行就行

补充:黑色节点左右子树为空,如果是添加到右子树,需要进行左旋转
补充:对应2-3树的三节点
补充:对应2-3树的四节点
补充:红色节点指的是,它和它的父亲节点是融合在一起的

注意:这里不准确,仅仅是便于理解颜色翻转,在添加数字66时,不会做翻转,然后在添加数字77时,才会进行颜色翻转,翻转完成后,根节点42是红色的,需要变成黑色的。
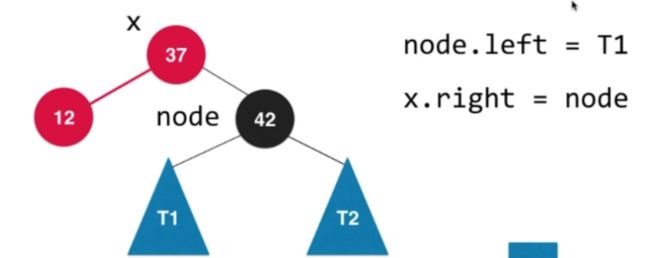
案例2:右旋转
场景:当左子树发生倾斜,进行右旋转
②添加数字37
黑色节点左右子树为空,直接把37添加进行就行

补充:对应2-3树的三节点
补充:对应2-3树的四节点
补充:红色节点指的是,它和它的父亲节点是融合在一起的

案例3:复合型
①基于37这个节点进行左旋转
②基于40这个节点进行右旋转
③右旋转结束后,交换颜色
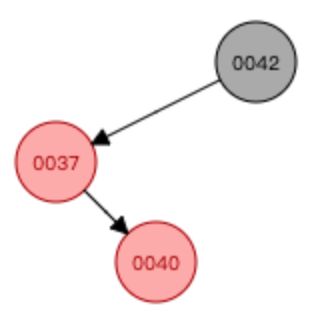
①先进行颜色翻转(当节点(0036)和父节点(0037)都是红色,节点叔叔也是红色时(0042),从祖父母(0040)那里压低黑度)
②然后根节点是黑色的
10.BTree
2-3树和2-3-4树就是B树
B树的阶:节点的最多子节点个树,比如2-3树的阶是3,2-3-4树的阶是4。
B-树的搜索:从根节点开始,对节点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子节点;重复,直到所对应的儿子指针为空,或已经是叶子节点。
关键字集合分布在整颗树中,即叶子节点和非叶子节点都存放数据,搜索可能在非叶子节点结束
其搜索性能等价于在关键字全集内做一次二分查找。

补充:假设检索15,先把磁盘块1加载到内存中,然后15与17和35比较,15比17小,然后基于P1子节点引用,P1是指向磁盘块2的一个指针地址,基于P1引用可以通过顺序IO快速加载磁盘块2.然后15与8和12比,15大于12,通过P3子节点引用,加载磁盘块7。然后命中,基于节点数据区加载数据。
补充:B-Tree首先是一个平衡树,平衡树的前提它是一颗搜索树或排序树
11.B+树
B+Tree树它是B-Tree数的变体,也是一种多路搜索树
B+Tree和B-Tree基本相同,区别在于B-Tree树非叶子节点和叶子节点都可以存放数据,而B+Tree树关键字存储在叶子节点上,非叶子节点不存真正的数据。
补充:
B+Tree非叶子节点只保存关键字和子节点引用(指向下一个叶子节点的指针)
叶子之间,增加了链表,获取所有节点,不再需要中序遍历;
所有的关键字都出现在叶子节点的链表中,且链表中的关键字(数据)恰好是有序的(即数据只能在叶子节点(稠密索引),因此不可能在非叶子节点命中)
非叶子节点相当于是叶子节点的索引(稀疏索引),叶子节点相当于是存储(关键字)数据的数据层
更适合文件索引系统
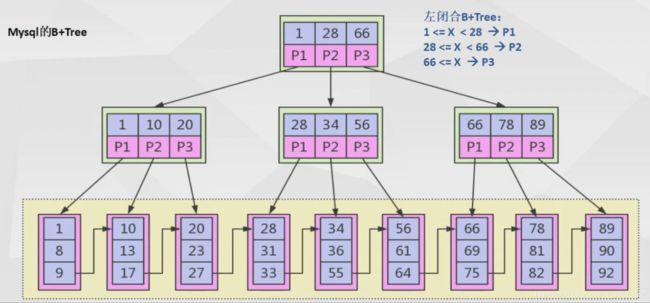
比如查找5,其实图顶端的5是索引,并不是真实数据,他会继续往下找。
这里把数据分成段,假如我们要找的数据是35,我们只需要找28指针下的所有子节点,这样5和65两块砍掉,这样砍掉的是2/3,而二分砍掉的是1/2。
补充:
B+Tree与B-Tree比较
B+Tree扫表和扫库能力更强(B-Tree树需要扫描整颗树,B+Tree树只需要扫描叶子节点)
B+Tree磁盘读写能力更强(叶子节点不保存真实数据,因此一个磁盘块能保存的关键字更多,因此每次加载的关键字越多)
B+Tree的排序能力更强
B+Tree的查询效率更加稳定(B-Tree树检索时间与关键字所在的树的高度有必然的关系,可能在第1层很快,可能在第3层或者更高层所耗时间会增加,检索效率不稳定,而B+Tree树每次都需要寻址到最后一层)