直观理解图像的傅里叶变换

由于不是专门的信号专业，当我我问很多身边的人怎么解释傅里叶变换时，很少有人能够理解，知道傅里叶变换是用来区分信号频率的这一层面已经算是比较难得了。在做数字图像处理时，图像的空间域和频率域相信也劝退了很多初学者，因此本文就从傅里叶变换的本质开始，逐步地对图像的傅里叶变换进行解释。

一、一维傅里叶变换

1.1 傅里叶变换的公式

傅里叶变换可以通过如下公式把信号 \(x(t)\) 从时域变换到频域：

\[X(w)=\int_{-\infty}^{+\infty}x(t)e^{-jwt}dt \]

看到这里估计很多人都会好奇，\(w\) 是哪来的？为什么要做在 \([-\infty, +\infty]\) 区间上对时间做积分？最后得到的信号 \(X(w)\) 表示什么东西？

1.2 傅里叶变换的本质

为了解决这个问题，我们首先了解一下欧拉公式：

\[e^{ix} = cos(x)+isin(x) \]

虚数 \(i\), 自然底数 \(e\) 在欧拉公式中通过一种完美的方式结合了起来。我们都知道，在复数空间中，\(m = a+bi\) 可以表示一个复平面的向量，它的大小为 \(|m|=\sqrt{a^{2}+b^{2}}\)，方向为 \(\theta = arctan(\dfrac{b}{a})\)。其实跟直角坐标系钟的表示差不多，只不过把 \(y\) 坐标系换成了虚数而已。那么进一步地，为什么会出现虚数呢？

我们都知道，虚数 \(i^{2}=-1\)，那么考虑在复平面内的一个向量 \(1+0i\)，如果将它乘上 \(i\)，那么原始向量 \(1+0i\) 就变成了 \(i+0\)，从复平面的角度来看，类似于逆时针旋转了 90°。所以，实际上虚数的出现是为了解决向量的旋转问题。

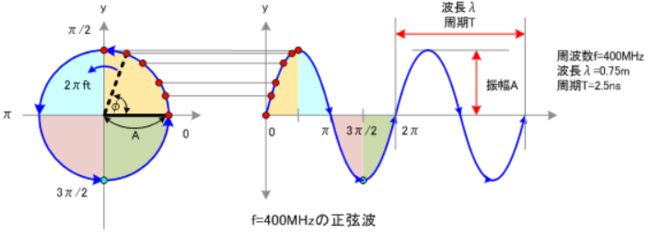
现在回过头来看一下欧拉公式，在任意位置 \(x = k\) 处，\(e^{ik}=cos(k)+jsin(k)\)，所以 \(|e^{ik}| = \sqrt{cos^{2}(k)+sin^{2}(k)}=1，\theta = arctan(\dfrac{sin(k)}{con(k)})\)，因此 \(e^{ix}\) 表示的就是一个复平面上的单位圆。假如 \(x\) 是时间 \(t\) 的函数 \(x=wt\)，那么欧拉公式可以写成：

\[e^{iwt} = cos(wt)+isin(wt) \]

此时动态地来看就相当于一个小球在复平面上绕着单位圆在做圆周运动，静态地来看就相当于将小球的位置在坐标系上进行了分解。

所以，傅里叶变换可以写成： $$ X(w)=\int_{-\infty}^{+\infty}x(t)cos(wt)-jx(t)sin(wt)dt $$ **傅里叶变换的本质就可以表示为，将原始信号乘上一组三角函数，之后在整个时间域上进行积分。**

1.3 傅里叶变换的频率选择

众所周知，傅里叶变换可以将时域信号的频率选择出来，选择的主要方式就是通过积分。比如：

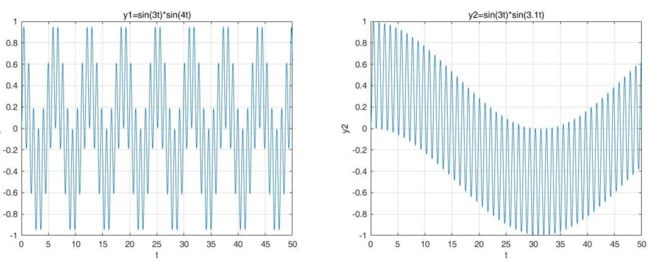
\(\int_{-\infty}^{+\infty}sin(3t)*sin(3t)dt\) 的结果的模接近于正无穷，而 \(\int_{-\infty}^{+\infty}sin(3t)*sin(4t)dt\) 的结果的模明显为0，因此我们将所乘上的正交函数的频率设置为变量 \(w\), 通过计算 \(w\) 所对应的模值大小便可以知道原始信号 \(x(t)\) 中存在哪些频率的信号。然而，现实中的信号都是有限的，因此不存在完全理想的状态，多少会有些出入，但是规律是一致的。

\(\int_{0}^{50}sin(3t)*sin(3.1t)dt=-4.7731，\int_{0}^{50}sin(3t)*sin(4t)dt=-0.0627\)

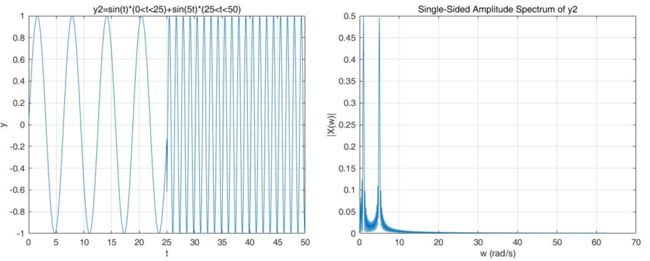
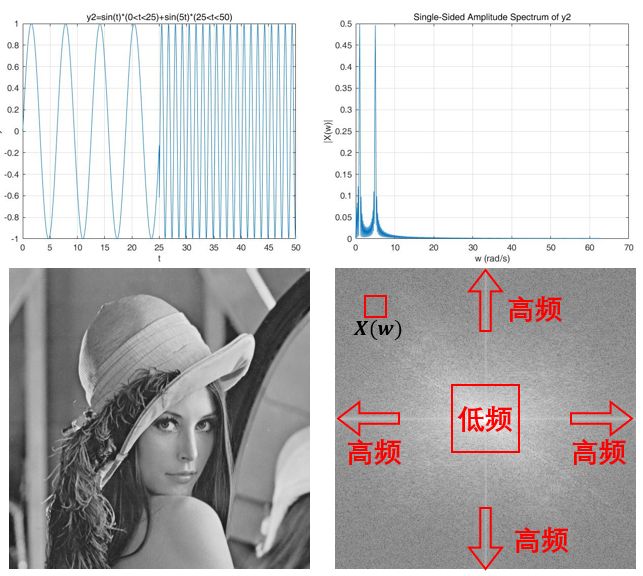
因此，相对于时域信号 \(x(t)=sin(t)(t\in[0,25])+sin(5t)(t\in[25,50])\)，其傅里叶变换的结果为（这里并没有体现出相位的关系）：

#### 1. 4傅里叶变换的直观理解

其实无论是时域信号还是频域信号，都是用来理解世界的一种方式，比如：在人的眼中可能事物是五颜六色的，这样能够很好地帮助我们理解这个世界。但是在蛇等动物的严重，可能事物只有红外这些，虽然都是同一个东西，但是理解的方式不一样，所感受到的东西也不一样。

再比如一段音乐，随着时间的播放会形成一段旋律，然而对于音乐家来说能够听出这段旋律中的音调，那么无论旋律在时域中多么优美，其实都是由一个又一个固定频率的音符组成。

因此，我们没必要将时域信号和频域信号进行一对一的等效，只需要理解这是不同看待信号的角度即可。

1.5 离散傅里叶变换（DFT）

刚刚提到过，由于实际的信号通常是离散且有限的，假设采集了 \(N\) 个信号点，其时刻为 \(\{t_{0},t_{1},...t_{N-1}\}\)，则对应时刻的信号为：\(\{x(t_{0}),x(t_{1}),...,x(t_{N-1})\}\)。首先我们将积分改成求和，得到：

\[X(w)=\sum_{i=0}^{N-1}x(t_{i})e^{-jwt_{i}} \]

然后我们采用相对采样时间间隔 \(n=\{0, 1, ..., N-1\}\) 代替真实采样时间 \(\{t_{0},t_{1},...t_{N-1}\}\)，得到：

\[X(w)=\sum_{n=0}^{N-1}x(n)e^{-jwn} \]

这样一来，\(X(w)\) 变成了以 \(2\pi\) 为周期的函数，因此积分区间可以从 \([-\infty, +\infty]\) 变成了 \([0, 2\pi]\)。进一步地，我们将积分区间离散化为 \(N\) 个采样点，则采样点之间的间隔可以表示为 \(\dfrac{2\pi}{N}\)。取 \(w = \dfrac{2\pi k}{N}, k=0,1,...,N-1\)，则有：

\[X(k)=\sum_{n=0}^{N-1}x(n)e^{-j\dfrac{2\pi k}{N}n}, k=0,1,...,N-1 \]

这便是离散傅里叶变换的公式了。

二、图像的傅里叶变换

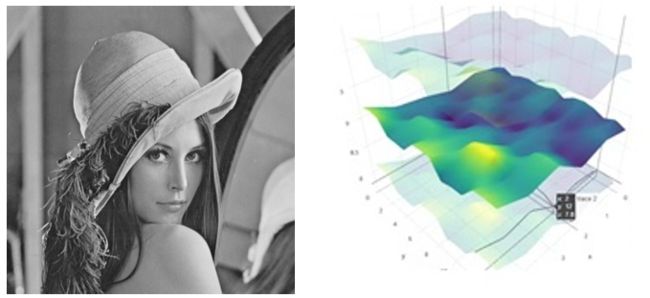
图像比如灰度图像其实也可以看成二维的离散信号，你可以想象一个三维坐标系，\(x,y\) 轴分别指示图像像素所在的位置，而 \(z\) 坐标系表示图像的像素值，于是，图像就可以表示如下：

于是，如果是图像中变化比较平坦的区域，那么在三维视角上该区域的频率就非常小，称为图像的低频信息（比如天空，大部分的地方的像素值都是相似的），而图像中变化比较剧烈的区域，则该区域的频率就比较大，称为图像的高频信息（比如上图中的头发部分，相邻近的地方像素值变化比较明显）。**因此，类似于一维信号的傅里叶变换，对图像进行傅里叶变换的目的就是把图像不同频率的信息进行分离。**如果说一维傅里叶变换的频谱图可以用一个二维空间表示，那么二维信号的傅里叶变换频谱就可以用一个三维空间表示，只不过这个三维空间的 $z$ 轴的坐标直接以灰度值的方式体现在了 $(x,y)$ 位置上：

因此，上图中的每个点到原点的距离描述的是频率，而不是图像的空间位置（像素位置），该点的灰度值 \(X(w)\) 描述的是频谱的幅度。

三、参考资料

https://zhuanlan.zhihu.com/p/66246381

https://zhuanlan.zhihu.com/p/99605178