PAT甲级题目翻译+答案 AcWing（树）

1020 Tree Traversals (25 分)

题意 ：

• binary tree二叉树；postorder and inorder traversal sequences后序遍历和中序遍历；level order traversal sequence层序遍历

思路 ：

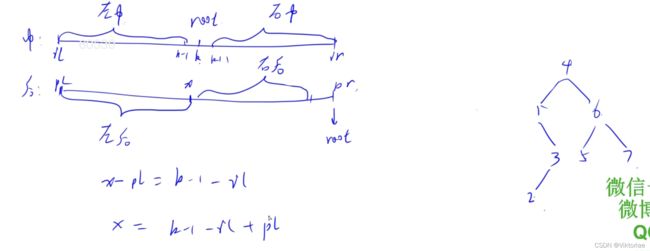
• 后序中找到根结点，中序中根结点左边是左子树，右边是右子树，知道了它们的长度就可以在后序中找到左右子树分别的根结点；这样就可以把整颗树重建；
• 用l和r两个哈希表记录每个根结点的两个儿子，也就是两个新的根结点
• 从根结点开始bfs，层序遍历
• $O(N)$，前提是所有权值不同；如果权值可能不同，对应的二叉树就不唯一了
• 有一个地方可以优化，如何找一个位置在中序遍历中出现的位置，先用哈希表存一下
• 三个哈希表建二叉树

语法 ：

• map中count是找左值是否存在

#include 
#include 
using namespace std;

const int N = 40;

int n;
int inorder[N], postorder[N];
int q[N];
unordered_map<int, int> l, r, pos;

int build(int il, int ir, int pl, int pr)
{
     
    int root = postorder[pr];
    int k = pos[root];
    if (k > il) l[root] = build(il, k - 1, pl, pl + (k - 1 - il));
    if (k < ir) r[root] = build(k + 1, ir, pl + (k - 1 - il) + 1, pr - 1);
    return root;
}

void bfs(int root)
{
     
    int hh = 0, tt = 0;
    q[0] = root;
    
    while(hh <= tt)
    {
     
        int t = q[hh ++ ];
        
        if (l.count(t)) q[ ++ tt] = l[t];
        if (r.count(t)) q[ ++ tt] = r[t];
    }
    
    cout << q[0];
    for (int i = 1; i < n; i ++ ) cout << ' ' << q[i];
    cout << endl;
}

int main()
{
     
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> postorder[i];
    for (int i = 0; i < n; i ++ )
    {
     
        cin >> inorder[i];
        pos[inorder[i]] = i;
    }
    
    int root = build(0, n - 1, 0, n - 1);
    bfs(root);
    
    return 0;
}

1021 Deepest Root (25 分)

题意 ：

• acyclic无环的
• 给一个无向图（n个点，n-1条边），如果不是树，输出图中连通块个数，否则，输出使树高度最高的所有根结点

思路 ：

• 如果只有一个连通块，那就是树
• 求连通块的数量，最好写的算法是 并查集
• $1s=10^8$，这道题是2s，可以算$2\ast 10^8$，且数据范围是$10^4$，所以可以暴力枚举，把每个点当作根，然后求最大深度$O(n)$
• 如果用bfs来求最大深度，就是求其他所有点到这个点的最短距离，如果用dfs就是求u到叶子结点的最大高度，递归求u的所有子结点到叶子结点中的max+1
• dfs的话，由于我们存的是无向边，所以我们从某个边往下搜的时候，从下面也会往上搜回来，所以我们要记一下当前这个点是从哪个点搜过来的，不要走回头路

#include 
#include 
using namespace std;

const int N = 1e4 + 10, M = 2 * N;

int n;
int h[N], e[M], ne[M], idx;
int fa[N];

int find(int x)
{
     
    if (fa[x] != x) fa[x] = find(fa[x]);
    return fa[x];
}

void add(int a, int b)
{
     
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int dfs(int u, int father)
{
     
    int depth = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
     
        int j = e[i];
        if (j == father) continue;
        
        depth = max(depth, dfs(j, u) + 1);
    }
    return depth;
}

int main()
{
     
    cin >> n;
    
    for (int i = 1; i <= n; i ++ ) h[i] = -1, fa[i] = i;
    
    int k = n;
    for (int i = 1, u, v; i <= n - 1 && cin >> u >> v; i ++ )
    {
     
        if (find(u) != find(v))
        {
     
            k -- ;
            fa[find(u)] = find(v);
        }
        add(u, v), add(v, u);
    }
    
    if (k > 1) printf("Error: %d components\n", k);
    else
    {
     
        vector<int> nodes;
        
        int max_depth = -1, depth;
        for (int i = 1; i <= n; i ++ )
        {
     
            depth = dfs(i, -1);
            if (depth > max_depth)
            {
     
                max_depth = depth;
                nodes.clear();
                nodes.push_back(i);
            }
            else if (depth == max_depth)
                nodes.push_back(i);
        }
        
        for (auto v : nodes) cout << v << endl;
    }
}

1043 Is It a Binary Search Tree (25 分)

题意 ：

• 给一棵树的先序遍历，判断它是否是二叉搜索树或者镜像二叉搜索树，如果是就yes，且输出这棵树的后序遍历，否则就输出no
• BST：左子树严格小于，右子树大于等于

思路 ：

• 我们发现BST的中序遍历（左子树，根，右子树）一定是有序的
• 因此，我们可以根据所给的前序遍历得到中序遍历，所以，问题转换成了给我们中序遍历和前序遍历，问是否是二叉搜索树
• 但是还是与前面的题有区别，前面的题保证了树上每个结点的权值 distinct，但这里不保证。看下列例子，8出现了2个，但在中序遍历中我们取的是左边那个8，因为BST定义左子树是严格小于当前根结点。因此，如果有多个相同值，一定要取第一个
• 那么什么时候无解呢，进行不下去，构造不成二叉树，就无解了；那么什么时候会构造不下去呢？在中序序列中找不到这个点就构造不下去了，直接return不合法即可
• 以上是判断在BST中是否合法，还要判断BST的镜像，镜像前中序遍历是从小到大，镜像后就是从大到小，相当于把整个树反转一遍，且注意在中序序列中找个根结点时，如果有多个相同的值，要找最后一个，因为要保证右子树中都比根结点小，也就是说从后往前找
• 建树过程中，如果中序遍历序列中已经没有数了，说明建树完成，成功；根据镜像与否，找到中序序列中当前根结点的位置，如果找不到，return false；如果能找到，接下来，递归建立左子树和右子树，如果都返回true，才是建树成功了；关键，在建树过程中完成了后序遍历（左子树，右子树，根）因此，是在最后将根放入postorder数组中

语法 ：

• 注意这个找k的方式，就可以在循环外继续使用这个找到的k了

#include 
#include 
using namespace std;

const int N = 1e3 + 10;

int n;
int preorder[N], inorder[N];
int postorder[N], cnt;

bool build(int il, int ir, int pl, int pr, int type)
{
     
    if (il > ir) return true;
    
    int root = preorder[pl];
    
    int k;
    if (!type)    // BST
    {
     
        for (k = il; k <= ir; k ++ )
            if (inorder[k] == root)
                break;
        if (k > ir) return false;
    }
    else        // mirror
    {
     
        for (k = ir; k >= il; k -- )
            if (inorder[k] == root)
                break;
        if (k < il) return false;
    }
    
    bool ok = true;
    if (!build(il, k - 1, pl + 1, k - 1 - il + pl + 1, type)) ok = false;
    if (!build(k + 1, ir, k - 1 - il + pl + 1 + 1, pr, type)) ok = false;
    
    postorder[cnt ++ ] = root;
    
    return ok;
}

int main()
{
     
    cin >> n;
    for (int i = 0; i < n; i ++ )
    {
     
        cin >> preorder[i];
        inorder[i] = preorder[i];
    }
    
    sort(inorder, inorder + n);     // 得到中序遍历序列
    
    if (build(0, n - 1, 0, n - 1, 0))
    {
     
        puts("YES");
        cout << postorder[0];
        for (int i = 1; i < n; i ++ ) cout << ' ' << postorder[i];
        cout << endl;
    }
    else
    {
     
        reverse(inorder, inorder + n);      // 翻转中序遍历序列
        
        cnt = 0;        // 重新建立后序遍历
        
        if (build(0, n - 1, 0, n - 1, 1))
        {
     
            puts("YES");
            cout << postorder[0];
            for (int i = 1; i < n; i ++ ) cout << ' ' << postorder[i];
            cout << endl;
        }
        else
        {
     
            puts("NO");
        }
    }
}