二叉树
二叉树的定义
二叉树是n(n>=0)个结点的有限集,它或为空树(n=0),或由一个根结点和两棵分别称为左子树和右子树的互不相交的二叉树构成。
二叉树是每个结点最多有两个子树的有序树,二叉树的子树通常被称为“左子树”(left subtree) 和 “右子树”(right subtree)。左、右子树的顺序不能互换。
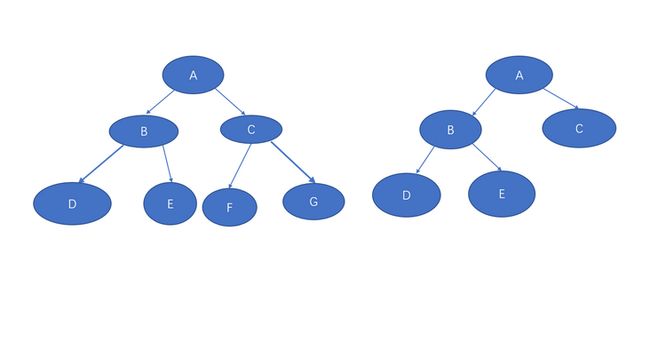
二叉树的各种形态
二叉树有不同的形态,按照对问题处理的一般情形和特例情形的分类处理原则,我们可以归纳分类出二叉树的五种基本形态和两种特殊形态,这样方便对二叉树进行讨论。
(1) 二叉树的基本形态,二叉树可以是空集: 根可以有空的左子树或右子树;或者左右子树皆为空。
(2) 二叉树的特殊形态:
① 满二叉树(Full Binary Tree)
满二叉树是除了叶结点外每一个结点都有左右子树且叶子结点都处在最底层的二叉树。或者, 如果深度为k的二叉树,有2的k次方-1个结点称为满二叉树。
②完全二叉树(Complete Binary Tree)
如果一棵树除最下层外,每一层的结点数均达到最大值,在最下一层要么是满的,要么在右边缺少连续若干结点(要求从最右边开始),则此二叉树为完全二叉树。如下图所示:
可以说满二叉树是完全二叉树的特殊情形。
基本操作
根据二叉树的逻辑结构定义,二叉树具有如下基本操作:
- 构造:建立一颗二叉树
- 查找:查找根结点、双亲结点、孩子结点、叶子结点等。
- 插入: 在指定位置插入结点
- 删除: 在指定位置删除结点
- 遍历: 沿着某条搜索路线,依次对二叉树中每个结点均做依次且仅做一次访问。
- 求深度: 计算二叉树的深度
链式结构及其基本实现
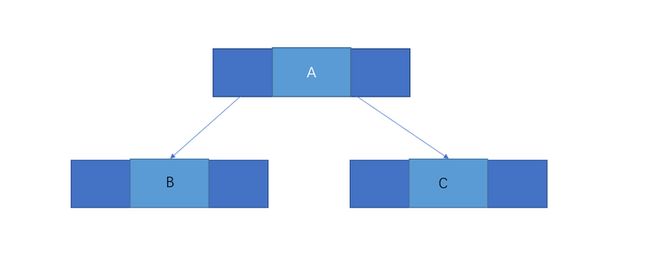
二叉链表
二叉树的每个结点含有两个指针域来分别指向相应的分支, 我们一般称之为二叉链表。
对应的数据结构描述:
public class BinaryTreeNode {
private int data;
private BinaryTreeNode leftTreeNode;
private BinaryTreeNode rightTreeNode;
}这种形式的二叉树,我们在拿到一个结点之后,便于获取它的孩子结点,获取它的父亲结点就颇为不易了,如果我们希望在获取到结点的时候,既能方便获取它的父亲结点,也能获取它的孩子结点呢?
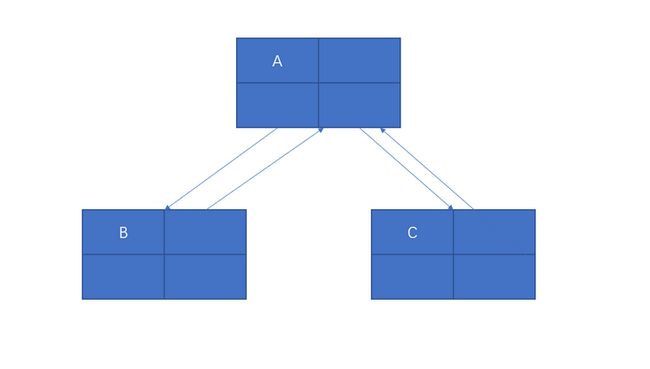
三叉链表
这也就是三叉链表,结点在存储孩子结点的时候,存储父亲结点的位置,如下图所示:
基本性质
二叉树的第i层至多有2i-1个结点(i >=1)
用归纳法证明: i = 1层,只有一个根结点,21-1= 2 0 = 1。
归纳假设对于所有的n,n >= 1, 命题成立。
归纳证明: 二叉树中每个结点至多有两个子树,则第n+1层的结点数2n-1 *2 = 2n。命题成立
深度为h的二叉树至多有2h-1个结点(h >= 1)
证明: 基于上一条性质,深度k的二叉树上的结点数至多为:
20+ 21+.....+2k-1=2k - 1.
对任何一颗二叉树,若它含有n0个叶子结点、n2个度为2的结点,则必存在关系式:n0 = n2 + 1 。
设n1为度为1的结点数。叶子结点的度为0,一颗二叉树度的取值只能为0,1,2
设二叉树上结点总数: n = n0 + n1 + n2。
二叉树的分支总数为: b = n1 + 2n2。
树中每个结点上都会有一个支路,但唯独有一个结点是例外--根结点。所以有b = n - 1 = n0 + n1 + n2 - 1。由此,n0 = n2 + 1。
- 具有n个结点的完全二叉树的深度为[log2n] + 1(方括号表示取整)
设完全二叉树的深度为k,则依据第二条性质得2k-1 <= n < 2k 即 k - 1 <= log2n < k. k只能是整数, 因此 [log2n ] + 1.
若对含n个结点的完全二叉树从上到下且从左至右进行1至n的编号,则对完全二叉树中任意一个编号为i的结点:
若i = 1, 则该结点是二叉树的根,无双。
若2i > n ,则该结点无左结点,否则编号为2i的结点为其左孩子结点。
若2i + 1 > n , 则该结点无右孩子结点,否则编号为2i+1的结点为其右孩子结点。
可用归纳法证明,编号为i的结点,如果有左结点,那么左结点的编号为2i, 如果有右结点为2i+1。
当i=1时,成立。
假设当i = n时成立,假设有左子结点, 编号为2n,假设有右子结点,编号为2n+1.
如果有左子结点,说明就有右子结点,因为是完全二叉树,这两颗结点相邻,所以编号为n+1的结点的左子树为2i+2,2i+3.
结论成立。
树的遍历
遍历(Traversal)--树的遍历(也称树的搜索)是图遍历(Graph Traversal)的一种, 指的是按照某种规则,不重复的访问某种树结构的所有结点的过程。具体的访问操作可能是检查结点的值、更新结点的值等。不同的遍历方式,其访问结点的顺序是不一样的。
在日常生活中树的遍历也是比较常见的:
例子1: 机电设备通电自检的简单模型
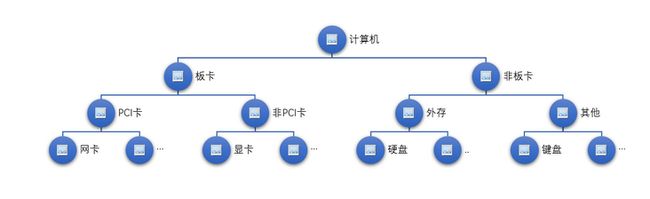
任何机电设备都是由若干零部件组成的。例如,计算机硬件由板卡、非板卡等一系列器件组成。可以按照计算机这样的组成分类建立起一个计算机硬件组成的二叉树(事实上是多叉树),如下图所示:
设备正常工作的前提是每个器件都正常工作,对于各个器件及其组成构件乃至整个设备的状态是否正常,显然从底层开始检测才是对的。
设备通电自检模型检测步骤:
- 步骤1:各器件(叶子结点)自检正常
- 步骤2: 对二叉树进行“后序遍历”直到根结点逐步检测。
- 步骤3: 如有错误信息则报错,否则显示设备正常。
- 步骤4: 结束。
具体的检测步骤如下:
- 左子树:网卡等正常 -> PCI正常 -> 显卡等正常 -> 非PCI正常 -> 板卡正常。
- 右子树: 硬盘等正常 -> 外存正常 -> 键盘等正常 -> 其他正常 -> 非板卡正常。
整棵树: 板卡正常 -> 非板卡正常 -> 计算机正常。
在上述的检测过程中,“后序遍历”的意思是指树的根结点是最后被访问到的,无论是整棵树还是左右子树。
例子2: 网购商品的管理
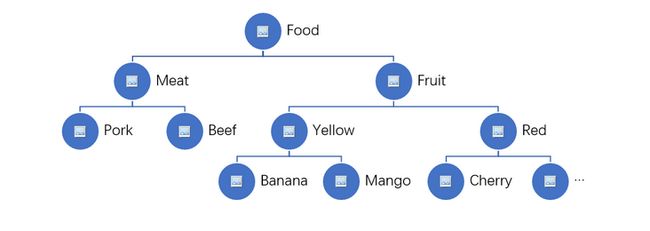
某在线食品店通过类别、颜色和品种来分类组织商品,分类图如下:
要通过程序自动的读出树形架构中的信息并把所有商品名称打印出来,应该怎么做才能做到清晰又没有遗漏呢?我们可以先列表来分析一下数据的规律, 如下图所示: 
由树到表格中每个结点的打印顺序规律是什么呢?
根结点: Food
左子树: Meat -> Pork/Beef
右子树: Fruit -> (左子树) Yellow -> Banana
Fruit -> (左子树) Red -> Cherry
打印的顺序是树的根结点最先被访问到,无论是整棵树还是左右子树。以这样的规律来访问树的结点,我们可以用一个词来称呼它--先序遍历。
按照搜索策略不同,二叉树的遍历可分为按广度优先遍历(Breadth-First Search) 和深度优先遍历(Depth-First Search)两种方式。
树的广度优先遍历
广度优先遍历是连通图的一种遍历策略,因为它的思想是从一个顶点开始,辐射状地优先遍历其周围直接相邻的广泛结点区域故得名。
二叉树的广度优先遍历又称为按层次遍历,从二叉树的第一层(根节点)开始,自上至下逐层遍历,在同一层中,按照从左到右的顺序对结点逐一访问。
树的广度优先遍历操作,是从根结点开始访问,然后以这个结点为线索,顺序访问与之直接相邻的结点(孩子)序列,然后下一步的广度遍历该以什么样的结点做开始的线索呢。
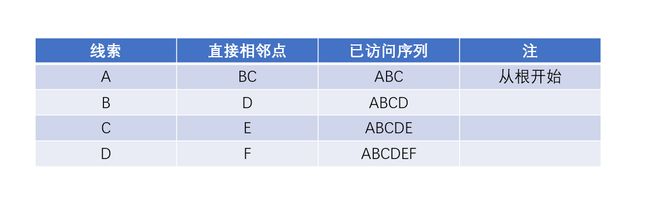
如下图所示, 首次被访问到的结点是A, 在链式存储结构上搜索A的直接相邻点,有B、C两个结点,则可以访问到的结点序列为ABC,下一次新的搜索结点从B开始,即以访问结点序列中第一个未做过线索的结点为线索,重复操作,直到所有的结点访问完毕。
上述的操作过程是一个线索结点不断在“已经访问序列”中被后移,新访问结点不断在“已访问序列”被添加的过程,因此,对“已访问序列”的操作过程就是一个队列的处理方法.先进先出。二叉树的数据结构如下图所示:
public class BinaryTreeNode {
private int data;
private BinaryTreeNode leftTreeNode;
private BinaryTreeNode rightTreeNode;
}队列add和offer的区别: add是抛出异常让你处理, offer是返回false
树的广度优先遍历:
/**
* 广度优先遍历
* @param root 根结点
*/
public static void levelOrder(BinaryTreeNode root) {
// LinkedList 实现了 Queue 我们用LinkedList来实现队列
LinkedList nodeQueue = new LinkedList<>();
// 根结点首先入队
nodeQueue.offer(root);
while (nodeQueue.size() > 0){
BinaryTreeNode node = nodeQueue.poll();
System.out.println(node.getData());
BinaryTreeNode leftNode = node.getLeftTreeNode();
if (leftNode != null){
nodeQueue.offer(leftNode);
}
BinaryTreeNode rightNode = node.getRightTreeNode();
if (rightNode != null){
nodeQueue.offer(rightNode);
}
}
} 二叉树的深度优先遍历
由二叉树定义可知,一颗二叉树由根结点、根结点的左子树和根结点的右子树三部分组成。因此对二叉树的遍历也可以相应的分解成三项“子任务”。
①: 访问根结点
②: 遍历左子树(即依次访问左子树上的全部结点)
③: 遍历右子树(即依次访问右子树上的全部结点)
因为左、右子树又都是二叉树(可以是一颗空的二叉树)。对它们的遍历可以按上述防范继续分解,直到每颗子树均为空二叉树为止。由此可见,上述三项子任务之间的次序。若以D、L、R分别表示这三项子任务,则有6种可能的顺序:
①: DLR ②: LDR ③: LRD ④: DRL ⑤: RDL ⑥: RLD
通常我们附带的限制是“先左后右”, 即子任务二在子任务三前完成,这样就只剩下三种次序:
- DLR--先根遍历(前序遍历)
- LDR--中根遍历(中序遍历)
- LRD--后跟遍历(或后序遍历)
三种遍历方法定义如下:
先序遍历: 先访问根结点D,然后按照先序遍历的策略分别遍历D的左子树和右子树。根结点最先访问,即每次遇到要遍历的子树,都是先访问子树的根结点。
通俗一点的解释就是: 如果我到达一个结点, 先打印当前结点,再去访问其他结点。
中序遍历: 先按照中序遍历的策略先遍历根D的左子树,然后访问根结点D,最后按照中序遍历的策略遍历D的右子树。根在中间访问。
通俗一点的解释就是: 当我到达一个结点的时候, 先判断当前结点的左结点是否为空,如果有就接着向下访问,没有的话就打印当前结点。
后续遍历: 先后序遍历根的左、右子树,然后访问根结点D,根在最后访问。
通俗一点的解释就是: 当我到达一个结点的时候, 先判断当前结点的左结点是否为空,如果有就接着向下访问,如果左子树为空就访问有结点,没有的话就打印当前结点。
从定义上来看这就是递归, 我们可以根据递归写出代码:
// 前序遍历
public void frontShow(BinaryTreeNode root){
System.out.println(root.getData());
if (root.getLeftTreeNode() != null){
frontShow(root.leftTreeNode);
}
if (root.getRightTreeNode() != null){
frontShow(root.rightTreeNode);
}
}
public void middleShow(BinaryTreeNode root){
if (root.getLeftTreeNode() != null){
frontShow(root.leftTreeNode);
}
System.out.println(root.getData());
if (root.getRightTreeNode() != null){
frontShow(root.rightTreeNode);
}
}
public void rightShow(BinaryTreeNode root){
if (root.getLeftTreeNode() != null){
frontShow(root.leftTreeNode);
}
if (root.getRightTreeNode() != null){
frontShow(root.rightTreeNode);
}
System.out.println(root.getData());
}栈是实现递归时最常用的辅助结构,利用一个栈来记录尚待遍历的结点, 以备以后访问,我们可以将递归的深度优先遍历改为非递归的算法。
(1) 非递归前序遍历
对于二叉树各结点的访问顺序是沿其左链一路访问下来,在访问结点的同时将其入栈,直到左链为空。然后结点出栈, 对于每个出栈结点,即表示该结点和其左子树已被访问结束,应该访问该结点的右子树。
- 准备一个临时变量指向根结点
- 打印当前结点, 当前临时变量指向左子结点并进栈,重复(2),直到左孩子为NULL
- 依次退栈,将当前指针指向右孩子
- 若栈非空或当前指针非NULL,执行(2),否则结束。
遇到一个结点,就访问该结点,并把此节点推入栈中,然后去遍历它的左子树。
代码示例1:
public void frontShowNoRecursion(BinaryTreeNode root) {
Stack stack = new Stack<>();
do{
while (root != null){
System.out.println(root.getData());
stack.push(root);
root = root.getLeftTreeNode();
}
if (!stack.isEmpty()){
root = stack.pop();
root = root.getRightTreeNode();
}
}while (!stack.isEmpty() || root != null); // 只要栈里面有元素或者root不为null都代表没结束
} 代码示例2:
public void frontShowNoRecursion2(BinaryTreeNode root) {
Stack stack = new Stack<>();
if (root != null){
stack.push(root);
while (!stack.isEmpty()){
BinaryTreeNode head = stack.pop();
System.out.println(head);
if (head.rightTreeNode != null){
stack.push(head.rightTreeNode);
}
if (head.leftTreeNode != null){
stack.push(head.leftTreeNode);
}
}
}
} 代码示例2的思路是: 先压入根结点, 因为栈是先进后出的, 先序遍历是 根 左 右,所以需要让右结点先入栈,然后再进入左结点。
(2) 非递归中序遍历
中序遍历的顺序是左 头 右 。 根据栈的特点为了实现这样的特性,越晚打印的我们越早入栈。遍历步骤为:
- 下一个结点不再有左子树的时候, 出栈每个结点都当作已经访问过其左子结点了,然后打印当前结点,然后用这样的方式访问当前结点的有子树。
public void middleShowNoRecursion(BinaryTreeNode head) {
Stack stack = new Stack<>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.leftTreeNode;
} else {
BinaryTreeNode node = stack.pop();
System.out.println(node.getData());
head = node.rightTreeNode;
}
}
} (3) 非递归后序遍历
后序遍历是左 右 根,也就是 3 4 2 6 7 5 1
头 右 左这种形式来遍历的话: 是 1 5 7 6 2 4 3 ,刚好是后序遍历的逆序形式。
头 右 左的遍历形式也就是先压左,再压右。 一个栈来收集头 右 左 这样形式的结点,另一个栈来收集头右左的出栈结点即可实现后序遍历。
代码示例1:
public void afterShowNoRecursion(BinaryTreeNode root) {
if (root != null) {
Stack s1 = new Stack<>();
Stack s2 = new Stack<>();
s1.push(root);
while (!s1.isEmpty()) {
BinaryTreeNode node = s1.pop();
s2.push(node);
if (node.leftTreeNode != null){
s1.push(node.leftTreeNode);
}
if (node.rightTreeNode != null){
s1.push(node.rightTreeNode);
}
}
while (!s2.isEmpty()) {
System.out.println(s2.pop().getData());
}
}
}
参考资料
- 《数据结构与算法分析新视角》 周幸妮 任智源 马彦卓 樊凯 编著