Example 1 For循环
考虑以下代码的时间复杂度是多少,使用Big Theta表示
public static void printParty(int N) {
for (int i = 1; i <= N; i = i * 2) {
for (int j = 0; j < i; j += 1) {
System.out.println("hello");
int ZUG = 1 + 1;
}
}
}选取一项最具代表性的操作
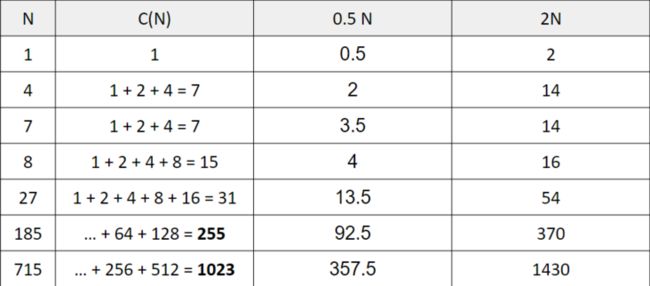
System.out.println("hello);记其执行次数为 c(N) ,枚举N从1 到 N,C(N)的值,用以下表格表示:
观察上下两个图可知
当N = 1时, i = 1, j = 0;
当N = 2时, i = 1 , 2, j = 0, 1;
N = 2,已知i = 1的结果,只需再求i = 2的结果再将前面算得的i = 1的结果相加,即 3 = 1 + 2
当N = 3时, 由于i的变化是每次变为 2i,即当N = 2时, 2i = 4,3比4小,循环仍然终止在N = 2,也就是说N = 3与N = 2的打印次数相同
......
因此观察得知,当N位于相邻的2的某指数幂之间时,打印次数与前一次相同,且等于前面所有2的指数幂时的打印次数相加,即
$$ C(N) = 1 + 2 + 4 + 8 + ...... + N $$
假设N为2的指数幂,那么上述式子共有 \( 1 + log_{2}N \)项
使用等比数列求和公式
$$ S_{n} = \frac{a_{1}(1 - q^{n})}{1 - q} $$
可算得:
$$ C(N) = \frac{1 - 2^{1 + log_{2}N}}{1 - 2} = 2N - 1 $$
因此 \( C(N) = \Theta(N) \)
技巧2
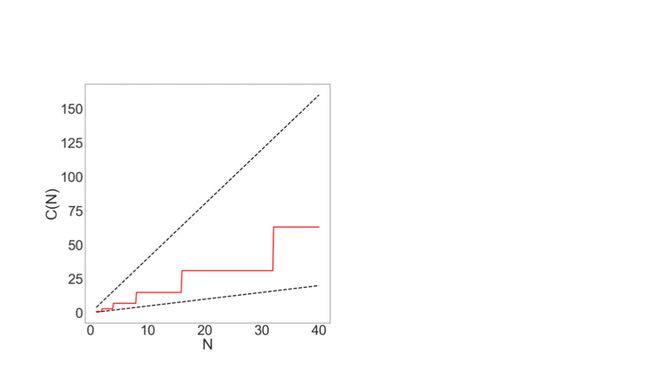
观察N的值可以发现,C(N)的值总是位于0.5N 到 2N之间,因此可以大致得出C(N)的函数图像:
不难发现\( C(N) = \Theta(N) \)
最后,Josh老师希望我们不要一看到for循环嵌套就认为时间复杂度是\( \Theta(N^{2}) \),还是要按部就班地分析,关于求时间复杂度的普遍性方法是
- 找出精确的和
- 写例子
- 画图
Example 2 递归树
考虑以下函数
public static int f(int n) {
if (n <= 1)
return 1;
return f(n-1) + f(n-1);
}时间复杂度是多少?
Solution 1
计算f(n)的调用次数c(n):
C(1) = 1
C(2) = 1 + 2
C(3) = 1 + 2 + 4
.......
C(N) = 1 + 2 + 4 + ... + \( 2^{N - 1} \)
因此根据等比数列前N项和可得 \(C(N) = 2^{N} - 1 \)
除了直接由等比数列前N项和得出结果之外,还可以由前面的公式
$$ C(Q) = 1 + 2 + 4 + ... + Q = 2Q - 1 $$
此处\( Q = 2^{N - 1} \),因此
$$ C(Q) = 2Q - 1 = 2 \cdot 2^{N - 1} - 1 = 2^{N} - 1 $$
也可以得出结果
因此时间复杂度 \(f(N) = \Theta(2^{N}) \)
Solution 2
从直观上来看,当f(n)中 n = 4时,f(4)的调用情况为
当n = 5时,f(5)的调用情况为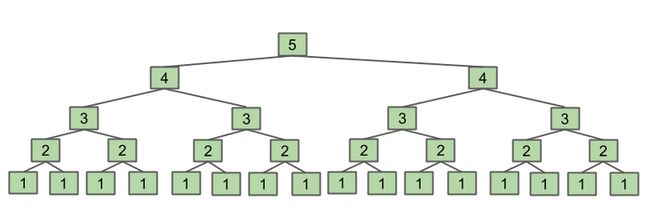
可见调用次数翻倍, n每增加1,调用次数 x 2,因此直观上来说也是\( 2^{N} \)指数级增加,更确切来说:
C(1) = 1
C(N) = 2C(N - 1) + 1
= 2(2C(N - 2) + 1) + 1
= 2(2(2C(N - 3) + 1) + 1) + 1
......
= 2(...2C(N - (N - 1)) + 1 ).... + 1
= 2^(N - 1)C(1) + 1 + 2 + 4 + ... + 2^((N - 1) - 1)
= 2^(N - 1) + 2^(N - 2) + 2^(N - 3) + ... + 4 + 2 + 1
= 2^N - 1时间复杂度 \(f(N) = \Theta(2^{N}) \)
Example 3 BinarySearch
接下来我们分析二分查找的时间复杂度,二分查找原理都应该比较熟悉了,不再过多介绍,具体实现过程可以查看这个slide BinarySearch Demo。
直观分析
我们知道的是每进行一次二分查找,其查找范围都会减半,也就是当前数组的大小减半,假设数组原始大小为 N ,最坏的情况下,直到数组大小缩短为 1 时,也就是只剩下一个元素时,我们才找到想要查找的值,那么,设二分查找的调用次数为C ,则
$$ 1 = \frac{N}{2^{C}} $$
从而解得
$$ C = log_{2}{N} $$
而对于二分查找,其函数体内执行次数均为常数阶,因此可以用调用次数来表示时间复杂度,从直观上来说 \(f(N) = \Theta({log_{2}N}) \)
精确分析
考虑以下问题:对于一个大小为6的数组,使用二分查找,其最坏的情况下,函数的调用次数是多少?
那么这是在N = 6时的情况 ,我们把N的所有情况与对应的函数调用次数C(N)列出: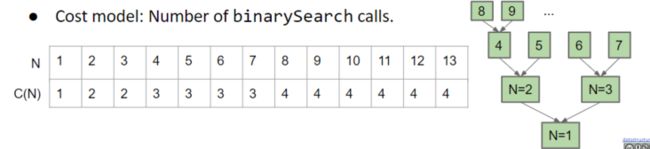
可见是一颗递归二叉树,观察可知
$$ C(N) = ⌊log_{2}(N)⌋+1 $$
我们得到了函数调用次数C(N)与数组大小N的精确关系,那么问题是
\( C(N) = \Theta(log_{2}N) \)吗?
证明:
$$ ⌊f(N)⌋=\Theta(f(N)) $$
proof:
$$ f(N) - \frac{1}{2} \le ⌊f(N) - \frac{1}{2}⌋ \le f(N) + \frac{1}{2} $$
根据Big Theta的定义,可知\(⌊f(N) - \frac{1}{2}⌋拥有下界f(N) - \frac{1}{2} 和上界f(N) + \frac{1}{2} ,属于f(N)函数簇\),因此
$$ ⌊f(N)⌋=\Theta(f(N)) $$
抛下常数阶,可知\( C(N) = \Theta(log_{2}N) \)
不加证明地,我们还能知道
$$ ⌈f(N)⌉=\Theta(f(N)) $$
$$ log_{P}(N) = \Theta(log_{Q}(N)) $$
因此以后无论是以任何常数为底的对数,都简写为logN,
因此最终化简结果是 \( C(N) = \Theta(logN) \)
另一种方法计算时间复杂度
考虑一下上面Example 2的一种利用式子本身的递归特性解题的方法,对于二分查找:
二分查找代码的瑕疵
当我们的二分查找实现代码为:
static int binarySearch(String[] sorts, String x, int lo, int hi)
if (lo > hi) return -1;
int m = (lo + hi) / 2;
int cmp = x.compareTo(sorted[m]);
if (cmp < 0) return binarySearch(sorted, x, lo, m - 1);
else if (cmp > 0) return binarySearch(sorted, x, m + 1, hi);
else return m;
}
存在一个瑕疵,当计算中间位置m的时候:
$$ m = \frac{(lo + hi)}{2} $$
\( 当 lo + hi > 2^{31} - 1 \)时,即超过了int 的最大值时,会发生溢出,导致m变成负数,从而引发数组ArrayIndexOutOfBoundsException
因此求中间位置的解决方案是
int mid = low + ((high - low) / 2);或者
int mid = (low + high) >>> 1;在C和C++中 没有 >>>,可以写成
mid = ((unsigned int)low + (unsigned int)high)) >> 1;细节非常重要!
参考
Example 4 MergeSort
本例分析归并排序的时间复杂度
归并排序即把一个数组一分为二,再二分为四,四分为八,直至缩小为一个数组只有1个元素,是一种典型的分治思想。之后再把数组从最底层的开始合并,合并的过程可以参考
MergeSortDemo
由于一次合并即相当于把大小为N的数组填充完毕,因此以填充次数而言,合并过程的时间复杂度为O(N)
直观分析
把一个大小为N的数组不断一分为二直至缩小为一个数组只有1个元素,如果进行了K次划分,那么
\(K = log_{2}N\)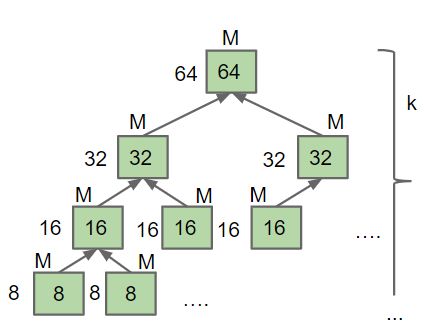
接着分析每一层的工作量,
第一层,需要将两个大小为N/2的数组合并,工作量为N
第二层,两个N/2的数组分别由两个N/4的数组合并而来,即4xN/4,工作量为N
......
观察知每一层的工作量均为N,共有K层,则总的工作量为
$$ f(N) = K\cdot N=Nlog_{2}N $$
使用递推的数学公式
因此,归并排序的时间复杂度为\(\Theta(NlogN)\)