十大排序(3)
今天我们学习10大排序的第三大类0(n)时间复杂度的排序
- 计数排序
- 桶排序
- 基数排序
1.计数排序
本节的排序我首先给出排序的步骤,然后,我们根据步骤对数据进行一次完整的排序模拟,然后总结该排序算法的性能。
算法步骤
- 找出待排序数组arr1的最大值和最小值(确定数字范围)
- 根据arr1数组值的范围确定辅助数组arr2对应范围内的下标所存储的值是0.
- 逐个遍历arr1数组,将每次遍历到的数据data作为arr2数组的下标,给arr2数组对应下标data对应的值加上1。
- 将arr2数组进行前缀相加(后面解释)
- 创建arr3保存最后排序好的数据,初始无数据。
- 逆序遍历原数组arr1,根据每次遍历到的value,作为arr2数组的下标,找到arr2数组的对应存储的数字data,此数字表示小于等于当前value的数字个数有data个。将value保存在arr3对应的data-1位置处。并更行arr2数组下标value对应值减去1。
- 最终arr3就是排序好的数据。
计数排序讲解起来十分的不方便,很多点不容易描述,需要举例子时时分析,希望大家可以帮忙总结下后面例子,反馈给我,谢谢各位。
示例模拟
1.假设班级有8名考生,考生成绩存储在arr1,成绩分别是2,5,3,0,2,3,0,3。
| arr1 | 2 | 5 | 3 | 0 | 2 | 3 | 0 | 3 |
|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
2.首先我们可以确定考生成绩的范围是0-5,然后根据范围创建新数组arr2,且arr2对应下标范围的数据都是0,就是指arr2[0]到arr2[5]保存的数据都是0,arr2数组创建多大其实无所谓,我们只关心你是否有下标0-5
| arr2 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
3.接着我们按照步骤,遍历成绩数组arr1,将每次遍历的数据作为arr2数组的下标,将对应下标的值加上1.例如arr1第一个遍历的是数字2,所以arr2[2]对应的值加上1,就是0+1=1,此处这样做的原因可以解释是,用arr2数组保存arr1每个数据出现的次数,例如arr2下标是0的数据是0,表示考0分的出现了0次。后面的依次类推。
| arr2 | 2 | 0 | 2 | 3 | 0 | 1 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
5.接着我们继续按照步骤,把arr2进行前缀相加处理。前缀相加就是从第二个位置的数据开始,每个数据等于自己加上前面一个位置的数据.这里前缀相加的作用其实就可以这样类比,下标是0的对应数据是2,表示分数小于等于0分的有2次出现,下标是1的还是对应数据2,表示分数小于等于2的有2次出现,综上所述,arr2数组就是统计原数据arr1每个数据出现的次数用的.
| arr2 | 2 | 2 | 4 | 7 | 7 | 8 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
6.接着我们按照步骤继续进行,创建arr3数组,arr3数据创建多大也无所谓,只要能保存下排序好的数据就行,我们就创建和原数据等长的数组.接着逆序遍历arr1数组,每次遍历到的数据data,作为arr2数组的下标,根据此下标找到arr2数组对应的数据,前面说过,arr2此时下标x对应的的数据y表示,小于等于成绩x的出现了y次.所以我们可以推断分数x前面有y个分数都小于等于自己,所以我们可以把数据x放在arr3数组的(y-1)位置上.因为数组下标是从0开始的,并同步更新arr2的x下标对应的y减去1,表示已经处理好了该数据的位置.
| arr2 | 0 | 2 | 2 | 4 | 7 | 7 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| arr3 | 0 | 0 | 2 | 2 | 3 | 3 | 3 | 5 |
|---|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
疑惑点解决
1.为社么要进行arr2数组前缀相加等后面没用的操作,当我们用arr2数组保存每个arr1值次数后,我们可以直接遍历arr2数组,就可以拿到排序好的数据了.比如步骤3完成后的arr2数组如下所示.
| arr2 | 2 | 0 | 2 | 3 | 0 | 1 |
|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
我们直接遍历过去,可以拿到数据0,0,2,2,3,3,3,5了,注意arr2数组的下标就是arr1的值,arr2数组的值保存的是对应下标出现的次数.
回答:为了维持数据的稳定性.当我说出来,估计有人不耐烦了,后面费这么大功夫.就是为了维持稳定性啊,是的,稳定性在这些数字看来不是那么重要,但是实际应用开发中,稳定性十分重要了.
总结
- 计数排序算法最差时间复杂度=最优时间复杂度=平均时间复杂度=0(n+k), k是数据范围。如果数据范围过大,耗内存就会巨大。
- 计数排序只适合数据范围较小的数据(核心)
- 计数排序是稳定的算法
计数排序代码
template
void Sort::sort_Count()
{
T min, max;
int i;
min = this->arr[0];
max = this->arr[0];
//找最小和最大值
for (i = 1; i < this->len; i++)
{
if (arr[i] < min)
{
min = arr[i];
}
if (arr[i] > max)
{
max = arr[i];
}
}
//按最小值和最大值创建数组
T *arr2 = new T[max - min + 1];
T num = 0 - min;//关键的一个数字
for (i = 0; i < max - min + 1; i++)
{
arr2[i] = 0;
}
for (i = 0; i < this->len; i++)
{
arr2[this->arr[i] + num]++;
}
//将数组前缀相加
for (i = 1; i < max - min + 1; i++)
{
arr2[i] = arr2[i] + arr2[i - 1];
}
//创建arr3,逆序遍历原数组,按值找到temp数组位置
T *arr3 = new T[this->len];
for (i = this->len - 1; i >= 0; i--)
{
T index;//标记arr2数组下标
index = this->arr[i] + num;
arr3[arr2[index] - 1] = this->arr[i];
arr2[index]--;
}
delete [] this->arr;
this->arr = NULL;
this->arr = arr3;
}
2.桶排序
桶排序我感觉是上面计数排序的一种,它绝对比计数排序好理解。毕竟计数排序太坑爹了,这加那加的。还是老规矩,先将计数排序的算法步骤,再举例子说明。
算法步骤
- 确定映射函数,映射函数就是将你待排序的数据尽可能均匀的分布在每个桶中
- 遍历待排序数组,按照映射函数,将元素放到每个对应的桶里
- 在给桶放入数据时,要保证这个桶内数据时有序的。为了保证每次插入数据有序,我选择用链表,因为链表插入数据简单,但是用二叉排序树更简单快捷。(插入后维持有序)
- 从第一个桶到最后一个桶逐个遍历,逐个取出数据。次数的数据就是有序的。
过程模拟
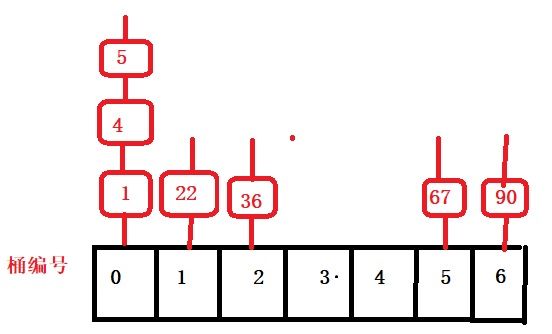
现在有数据22,4,36,1,67,90,5我们来按照步骤逐个进行模拟。
- 我在网上查找到一个较为通用的映射函数hash = 每个数据*数据个数/(数据的最大值+1),这个可以哈希函数可以让数据保证映射在0到(数据个数-1)的范围里。所以可以分配给桶的编号是0到(数据个数-1).
2.依次对这几个数据进行哈希值计算,算出的结果就是对应桶的编号,将次数据插入该桶中,并保证桶时时有序。
hash(22) = 22*7/(90+1) = 1
hash(4) = 4*7/(90+1) = 0
hash(36) = 36*7/(90+1) = 2
hash(1) = 1*7/(90+1) = 0
hash(67) = 67*7/(90+1) = 5
hash(90) = 90*7/(90+1) = 6
hash(5) = 5*7/(90+1) = 0
3.依次取出桶中的数据就是1,4,5,22,36,67,90.可以发现数据次数是有序排列的。
总结
- 桶排序思路简单,但是核心要领就是映射函数选择恰当。
- 桶的个数接近于待排序元素的个数时,时间复杂度最低,最好。
- 桶排序多应用于外部排序中。
- 最好时间复杂度=平均时间复杂度=0(n+k),最坏复杂度是0(n^2)
最坏的情况就是,映射函数设计不合理,所有数据堆积到一个桶,所有数据遍历一遍,还要再桶里面排序就是0(n^2)了 - 桶排序是稳定的算法
桶排序代码
template
void Sort::sort_Bucket()
{
int i,j;
T max, hash;
Node *table,*p, *q, *temp;
max = arr[0];
table = new Node[this->len];//桶
for (i = 1; i < this->len; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
table[i].next = NULL;//初始化桶
}
table[0].next = NULL;
//遍历数组,分别入桶
for (i = 0; i < this->len; i++)
{
hash = (arr[i] * this->len) / (max + 1);
if (table[hash].next == NULL)
{
temp = new Node;
temp->data = this->arr[i];
temp->next = table[hash].next;
table[hash].next = temp;
}
else
{
temp = new Node;
temp->data = this->arr[i];
q = &table[hash];
p = table[hash].next;
while (p != NULL && p->data <= temp->data)
{
q = q->next;
p = p->next;
}
if (p == NULL)
{
temp->next = p;
q->next = temp;
}
else {
temp->next = p;
q->next = temp;
}
}
}
//遍历桶,取出数据
j = 0;
for (i = 0; i < this->len; i++)
{
p = table[i].next;
while (p != NULL)
{
this->arr[j++] = p->data;
p = p->next;
}
}
}
3.基数排序
基数排序是一个十分容易理解的算法,可算遇到这种容易上手的算法了.它就进行简单的数据入桶和数据出桶操作.每个桶的编号对应0-9,因为数字只能是0-9组成了.
算法步骤
- 找出待排序数据的最大值,确定它的位数,例如78的位数就是2,101的位数就是3.
根据这个最大值的位数我们可以确定入桶和出桶的次数了. - 逐个遍历原数据,第一次根据每个数据的个位数进行入桶,例如数据78,它的个位数是8,那么数据78就被放在编号是8的桶中.待所有数据按照个位数放在对应的桶中时,在依次从0号桶到9号桶逐个的取出数据,每次都将桶数据全部取出来,逐个放回原数据.
- 根据步骤一的位数,我们知道了入桶的次数,第二次就根据原数据的十位数,进入对应编号的桶里面,假设数据78,它第二次就进入桶7里.待所有数据都入桶后,再逐个从0号桶到9号桶逐个取出数据,再放回原数据.假设位数是2,次数就结束了,因为已经入桶两次了,次数的数据就是有序的,假设位数是3,那么还需进行一次入桶,按照百位数入对应的桶,再取出来.
过程模拟
待排序数据是22,6,8,100,78,5,1,下面我们将按照步骤依次进行.
1.找出最大数是100,它的位数是3,我们需要进行3次入桶操作.先是数据22,它的个位数是2,放入2号桶,接着是数字6,个位数是6,放入6号桶,继续操作,直到数据放完.
| 78 | ||||||||||
| 100 | 1 | 22 | 5 | 6 | 8 | |||||
| 桶编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
2.将桶中数据从0号桶到9号桶依次取出来,放回原数组.注意每个桶取出的顺序只能是从下往上取出来,取出后的数据如下表格.
| 数据 | 100 | 1 | 22 | 5 | 6 | 8 | 78 |
|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
3.次数只是第一次入桶的完成,接着把数组逐个按照十位数进行入桶操作,例如78放在桶7里面.
| 8 | ||||||||||
| 6 | ||||||||||
| 5 | ||||||||||
| 1 | ||||||||||
| 100 | 22 | 78 | ||||||||
| 桶编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
4.从桶里面逐个取出数据,放回原数组里
| 数据 | 100 | 1 | 5 | 6 | 8 | 22 | 78 |
|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
5.继续进行第三次入桶操作按照百位数进行入桶.
| 78 | ||||||||||
| 22 | ||||||||||
| 8 | ||||||||||
| 6 | ||||||||||
| 5 | ||||||||||
| 1 | 100 | |||||||||
| 桶编号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
6.从0号桶到9号桶逐个取出桶中全部数据
| 数据 | 1 | 5 | 6 | 8 | 22 | 78 | 100 |
|---|---|---|---|---|---|---|---|
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
7.排序完成,就是这么爽.
总结
- 基数排序的使用场合:排序的项目是具有大范围但几位数的整数
- 最好时间复杂度=最差时间复杂度=平均时间复杂度=0(n*k)=0(n)
- 基数排序是稳定的算法
基数排序代码
template
void Sort::sort_Radix()
{
//1.找出最大数
T max;
int i,count;
max = this->arr[0];
for (i = 0; i < this->len; i++)
{
if (this->arr[i] > max)
{
max = arr[i];
}
}
//2.确定最大数的位数
count = 0;
while (max != 0)
{
max = max / 10;
count++;
}
//3.从最低位开始逐个放数据,取数据
Array * arr = new Array[10];//存放0--9的桶
for (i = 0; i < 10; i++)
{
arr[i].data = new T[this->len];//每个桶的最大容量就是待排序数据
arr[i].len = this->len;
}
for (i = 0; i < count; i++)
{
}
}