对于树这个数据结构,第一次看到这个树肯定是一脸蒙逼,玛德,树?种树的那个树么?哈哈哈,当然不是,前面我们说过数组添加、删除数据很慢,查询数据很快;而链表添加、删除数据很快,但是查找数据很慢,我们就想啊,有没有一种数据结构取二者之精华,那不就是一个添加,删除,查询都很快的数据结构吗?那用起来多舒服啊!
这个取二者之精华的数据结构就是树(tree),而且随着各种大佬对树这种结构的改进,就有了很多种树,常见的有二叉树,红黑树,2-3-4树等各种树,我们就一起看看这几种简单树到底是什么鬼!
进群:697699179可以获取Java、大数据各类入门学习资料!
这是我的微信公众号【编程study】各位大佬有空可以关注下,每天更新Java、大数据学习方法,感谢!
学习中遇到问题有不明白的地方,推荐加小编Java|大数据学习群:697699179内有视频教程 ,直播课程 ,等学习资料,期待你的加入
1.树的基本概念
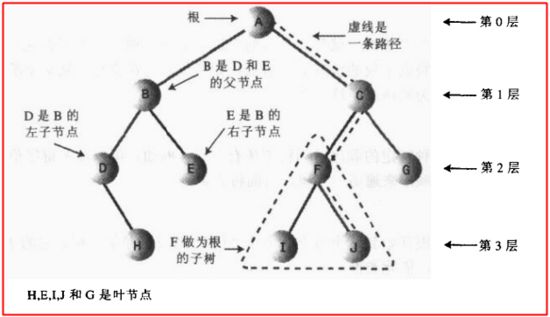
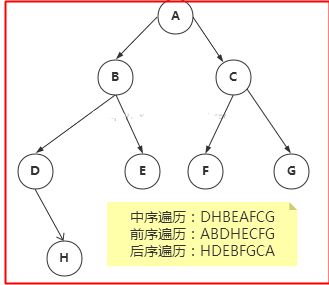
树的基本结构就是由一个个的节点组成,如下图所示,然后每一个节点都通过边相连,那么有人要问了,这些节点是什么啊?emmm...上篇博客实现了链表,就是类似链表的那个节点一样的东西,本质上就是一个Node的实例,在这个实例中,有几个属性,分别几个子节点和其中保存的数据;
这里注意一下,任意一个节点的父节点只能有一个,子节点可肯能有多个;这很好理解,现实中,你可以有多个孩子,但是你能有多个亲爹吗???
比如对于B节点来说,A是父节点,D,E,F都是子节点,而对于没有子节点的那种节点,叫做叶节点,这里的D、E、F、G、H都是叶节点;由于一切节点都是从A出发的,所以A叫做根节点
注:第一次看这个图是不是不觉得像一棵树啊,其实你要把这个图旋转180度,倒过来看就比较像一棵树了,哈哈哈!话说用过linux操作系统的人应该知道linux的各种目录"/"就是树结构。。。
那么什么是二叉树呢?这很简单,每个节点最多只能两个子节点,我们看看下图,这就是一个二叉树的基本结构
根据上图,我们说一下树的基本术语:
路径:从任意一个节点到另外任意一个节点所经过的节点的顺序排列就是路径;
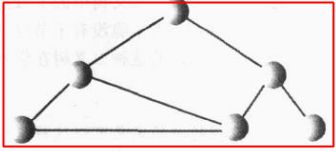
根节点:一棵树只有一个根节点,要保证根到任意一个节点只有一条路径,否则就不是树了,比如下图这个就不是树
父节点:与当前节点连接的上一层节点就是父节点
子节点:与当前节点连接的下一层节点就是子节点
叶节点:没有子节点的节点就是叶结点
子树:上图中在树中随便找一个节点B当作根节点,然后B的所有子节点,子节点的子节点等等就构成了一个子树;
左/右子节点:由于二叉树的每一个节点都只有两个节点,于是左边的子节点叫做左子节点,右边的就叫做右子节点;
2.二叉搜索树
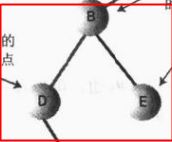
什么是二叉搜索树呢?其实就是一种特殊的二叉树,只是我们向其中添加数据的时候定义了一种规则,比如下图B中存了数据20,现在我们要添加数据10和30,应该怎么放呢?我们将小于20的数据放在左子节点,大于20的数据放在右子节点,这就是二叉搜索树,树如其名,搜索起来特别快;
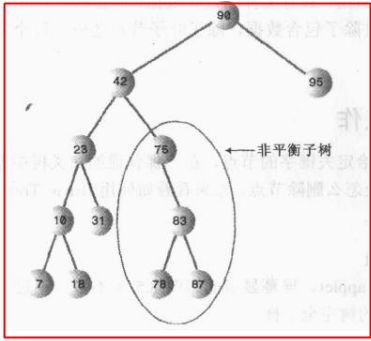
顺便提一下平衡树和非平衡树,数据在左右子节点中分布比较平均就是平衡树,不怎么平均的就是非平衡树,下图所示,76这个节点只有一个右子节点,而且还连着这么多数据,有点不平衡....
下面我们简单用java代码来表示树的节点(还是用静态内部类的形式):
2.1.添加节点
添加节点的时候要准备两个指针,parentNode=null和current=root,首先我们要判断root是不是为null,如果是的话直接将我们要添加的节点newNode放到第一个节点就ok了;
假如有root节点之后再要添加新的节点,先让parentNode指向current节点(就是root节点),current这个指针指向哪里就必须要判断newNode和root中数据的大小,如果newNode大,则current就指向左子节点,反之则指向右子节点;同时会判断左子结点或者右子节点是否存在,不存在的话直接将newNode放到该位置即可,存在的话继续执行while循环;具体代码如下:
publicbooleanadd(intvalue){ Node newNode =newNode(value);if(root==null) { root = newNode;returntrue; }else{ Node parentNode =null; Node current = root;while(current!=null){ parentNode = current;if(value
2.2.遍历树
我们要查看一下树中的所有节点中的数据,就需要我们实现对树中所有节点的遍历,这个遍历方式有很多种,每个节点最多有两个子节点,可想而知最容易想到的方式就是递归;
最常见的三种遍历方式:前序、中序、后序,其中重点是中序,最后会按照从小到大的顺序打印出来:
前序:根节点-----左子树-------右子树
中序:左子树-----根节点--------右子树
后序:右子树-------根节点--------左子树
三种方式分别用代码来实现为 , 最重要的是中序 ;
//中序遍历publicvoidinfixOrder(Node current){if(current !=null){ infixOrder(current.leftChild); System.out.print(current.key+" "); infixOrder(current.rightChild); }}//前序遍历publicvoidpreOrder(Node current){if(current !=null){ System.out.print(current.key+" "); preOrder(current.leftChild); preOrder(current.rightChild); }}//后序遍历publicvoidpostOrder(Node current){if(current !=null){ postOrder(current.leftChild); postOrder(current.rightChild); System.out.print(current.key+" "); }}
好好想想这里中序的递归。。。。
2.3.查找节点
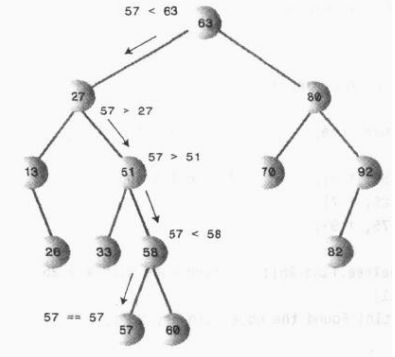
比如下面这个图中要查找57这个节点是否存在,我们首先将57比63小,我们就把57和左子结点27比较,57大;然后57在和51比较,再就是和58比较,小于58再和左子结点57比较,相等的话就返回这个57的节点
用代码来实现原理:
publicNodefind(Integervalue){ Node current = root;while(current!=null){if(valuecurrent.key){ current = current.rightChild; }else{returncurrent; } }returnnull; }
2.4.最大值和最小值
假如我们要找树中的最大值和最小值还是很容易的,因为树中的数据都是按照了规则放的,最小值应该就是最左边的子节点,最大值应该就是最右边的字节点,我们也用代码来看看:
//查询树中最大值publicNode findMax(){ Node current = root; Node max=null;while(current!=null){ max = current; current = current.leftChild; }returnmax; }//查询书中最小值publicNode findMin(){ Node current = root; Node min =null;while(current!=null){ min = current; current = current.rightChild; }returnmin; }
这里的max和min两个指针比较关键,因为当跳出while循环的时候,curent肯定是为null,但是我们想要打印出这个current的父节点,于是我们可以用这两个指着保存一下;
其实到这里一个树的基本结构和功能就差不多了,可以自己测试一下;
2.5.删除节点
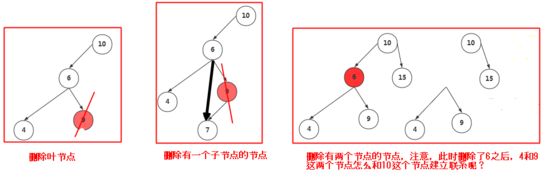
删除节点最后说,为什么呢?因为删除节点最复杂,你想啊,节点是分为很多种的,假如删除的是叶节点那很容易,直接将这个叶节点的父节点对它的引用变为null就行了,但假如要删除的节点是中间的节点呢?这就比较麻烦了,这个中间节点又分为有一个子节点,两个子节点,对于有一个子节点的很好处理,但是两个子节点的就最麻烦!
我们重点看看第三个图,删除的节点又两个子节点的时候,肯定要想一个新的节点去代替那个6节点,使得整个树不破坏结构,还是可以正常使用,这种方式叫做找后继节点,顾名思义就是找6那个节点后面的节点来代替6节点,而且必须是6节点的右子节点(想象为什么呢?),我们慢慢看有哪几种后继节点满足要求;
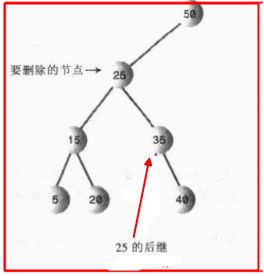
第一种:被删除节点的右子节点的左节点,下图所示的30就满足条件啊;而且这给了我们一个启发,这种的后继节点就是找一个比被删除节点大一点点的节点;换句话来说,就是在被删除节点的右子节点中找最小的节点;
第二种:被删除节点的右子节点只有一个右子节点,说起来很绕,看图,我们直接将35作为新的节点放在被删除节点25的位置就可以了,其他的不动;
现在我们总结一下删除节点所需要的重点:
(1).删除的节点是叶节点,我们找到该叶节点的父节点,修改父节点指向叶结点的引用为null即可;
(2).删除的节点有一个子节点
2.1.这个子节点是左子结点
2.2.这个子节点是右子节点
(3).删除的节点有两个子节点,这种就要找后继节点来补上被删除节点的那个位置,防止树的结构被破坏,找后继节点就是找被删除节点的右子节点中最小的值
3.1.被删除的节点的右子节点只有右子节点的话,就直接将右子节点变为后继节点;
3.2.被删除的节点的右子节点有两个子节点的话,找这两个子节点中的最小值即可;即使这两个子节点后面还有子节点,也是一样的找最小值
既然思路已经理清楚了,那就用代码来表达出来,比较多:
//根据数据删除对应的节点publicboolean delete(int value){ Nodeparent=null; Node current = root; Boolean isLeftChild =null;//当根节点不存在的时候,执行删除操作会抛出异常if(root==null) {try{thrownewException("树中没有数据,你删除空气啊!"); }catch(Exceptione) { e.printStackTrace(); }returnfalse; }//这里只是移动了parent和current的指针,首先是判断节点是在根节点的左边还是右边,确定了之后再慢慢往下找,最后将current移动到被删除的节点那里,//后面我们就可以通过current这个指针获取删除节点的信息;//如果最后current==null了,说明最后没有找到该节点,就返回falsewhile(value!=current.key){parent= current;if(value
所有的逻辑就这么多,我们可以把所有的代码整理一下,并且测试一下结果,成功;
package com.wyq.test;import com.wyq.test.MyTree.Node;publicclassMyTree{privateNode root;publicstaticclassNode{privateInteger key;//节点中存的数据privateNode leftChild;//左子结点privateNode rightChild;//右子节点publicNode(Integer key){this.key = key;this.leftChild =null;this.rightChild =null; }publicvoiddisplayNode(){ System.out.println("{"+key+"}"); } }publicbooleanadd(intvalue){ Node newNode =newNode(value);if(root==null) { root = newNode;returntrue; }else{ Node parentNode =null; Node current = root;while(current!=null){ parentNode = current;if(valuecurrent.key){ current = current.rightChild; }else{returncurrent; } }returnnull; }//查询树中最大值publicNodefindMax(){ Node current = root; Node max=null;while(current!=null){ max = current; current = current.leftChild; }returnmax; }//查询书中最小值publicNodefindMin(){ Node current = root; Node min =null;while(current!=null){ min = current; current = current.rightChild; }returnmin; }//根据数据删除对应的节点publicbooleandelete(intvalue){ Node parent =null; Node current = root; Boolean isLeftChild =null;//当根节点不存在的时候,执行删除操作会抛出异常if(root==null) {try{thrownewException("树中没有数据,你删除空气啊!"); }catch(Exception e) { e.printStackTrace(); }returnfalse; }//这里只是移动了parent和current的指针,首先是判断节点是在根节点的左边还是右边,确定了之后再慢慢往下找,最后将current移动到被删除的节点那里,//后面我们就可以通过current这个指针获取删除节点的信息;//如果最后current==null了,说明最后没有找到该节点,就返回falsewhile(value!=current.key){ parent = current;if(value
3.关于删除数据的一点思考
上面的删除方法可谓是很长而且逻辑很容易弄混,那有没有方法避免这种有点坑的东西呢?
于是啊,我们就想到一个办法,我们把删除节点不是真的删除,是逻辑删除;比如相当于给这个节点添加一个属性isDelete,这个状态默认为false表示这是一个正常的节点,如果我们要删除某个节点,只需要把isDelete变为true,代表着这个节点已经不属于这个树了,这种做法的好处就是不会改变这个树的结构,可以想想这种做法和之前删除的做法的区别;但是坏处也很明显,就是删除的节点也会保存在树中,当这种删除的操作很多的时候,树中就保存了太多垃圾数据了,所以看情况使用。。。
4.关于节点中数据的一点改进
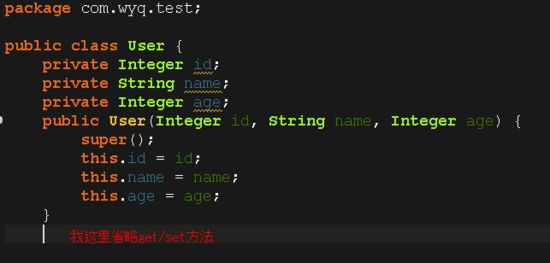
有没有看到我们上面实现的树中的节点中保存的数据都是数字啊,为什么呢?因为简单呗,很容易理解,如果把树中节点的数据换成对象其实也是行的,比如下面这样的:
如果是这样的话,我们添加数据就必须要按照User对象的某个属性(比如id)为关键字进行比较,然后向树中插入数据,其实跟我们用Integer尅行的差不多,只是写起来代码看起来不够简洁;
下图选取部分代码进行修改:
5.总结
树这种数据结构还是挺厉害的,杂糅了数组和链表的有点于一身,查找数据很快,增加和删除数据也很快,但就是特么的理解其中的逻辑需要一点点时间去慢慢啃。。。。。后面还有各种树!
下一篇应该是红黑树了,加油加油!.