数据结构与算法 —— 剑指offer
牛客的剑指题目:https://www.nowcoder.com/ta/coding-interviews
0、Python基础语法知识
0. 1. split()函数用法
0. 2.字符串的读取
0. 3.字典的基础知识
0.3.1.字典的基本操作
dict = {"a" : "apple", "b" : "banana", "c" : "grape", "d" : "orange"}
#输出key的列表
dict.keys()
输出:dict_keys(['a', 'b', 'c', 'd'])
#输出value的列表
dict.values()
#每个元素是一个key和value组成的元组,以列表的方式输出
dict.items()
输出:dict_items([('a', 'apple'), ('b', 'banana'), ('c', 'grape'), ('d', 'orange')])
0.3.2.字典的遍历
for k in dict:
print ("dict[%s] =" % k,dict[k])
输出:
dict[a] = apple
dict[c] = grape
dict[d] = orange
dict[w] = watermelon
for (k, v) in dict.items():
print ("dict[%s] =" % k, v)
输出:
dict[a] = apple
dict[c] = grape
dict[d] = orange
dict[w] = watermelon
0.3.3.字典值的获取
dict["a"]
输出:'apple'
dict["a"][0]
输出:'a'
字典的增加:
dict["w"] = "watermelon"
dict输出为:{'a': 'apple', 'b': 'banana', 'c': 'grape', 'd': 'orange', 'w': 'watermelon'}
字典的删除:
dict.pop("b")
输出为:'banana'
0. 4. 拼接为字符串
-
可以直接用+,具体题目见《左旋转字符串》
-
采用 join() 函数。
s = ['s', 'd', 's', 'd', 'v', 'f', 'h', 'b', 'f', 'g', 'h', 'N', 'I', 'O']
s = ''.join(s)
输出:'sdsdvfhbfghNIO'
0. 5. 删除首位空格
str.strip()
0. 6. 将两个数组变成一个数组
- A+B
- A.extend(B)
0. 7. isalnum()和lower()
lower():转换字符串中所有大写字符为小写。
isalnum():检测字符串是否由字母和数字组成。
0. 8.
数据转换为字符串,再逆序输出:int(str(x)[::-1])
1、链表剑指题目
节点的定义
class item (object):
def __init__(self, data):
self.data = data
self.next = None
1. 1. 从尾到头打印链表:
- a[i:j:s],从i到j,按步长s输出。输出长度为j-i-1,且不包括元素j。例如:A[::-1]表示涉及的数字倒序输出。
- Insert可以在指定的位置插入具体的元素。
- res.reverse()表示反转,不能在链表中直接使用。
class Solution:
# 返回从尾部到头部的列表值序列,例如[1,2,3]
def printListFromTailToHead(self, listNode):
# write code here
cur = listNode
res = []
while cur:#while循环后接的要与下面的对应,要么都为cur,要么都为listNode。
res.append(cur.val)#不能插入cur,而是要插入cur.val。
cur = cur.next
return res[::-1]
1. 2. 合并两个排序的链表
链表为dum={1,2,3,4},则dum.next = {2,3,4}
- 一定要注意判断两个链表是否为空的情况。
- 若链表为空,不能用0,而是None。
- sort()函数不能在链表中直接使用。
- pHead1.next表示下一个节点。
- 算法流程图如下:
- cur一定要向前走,否则的话新链表就无法往后走了。

cur = tmp = ListNode(0)#伪头结点的设置
1. 3.两个链表的第一个公共结点(双指针)
解题思路:见双指针
主要是注意当两个链表没有公共点,且链表长度不相等时,如果不相交说明两个指针走过的次数都为m+n,他们会同时到达链尾,也就是它们同时会指向NULL,达到跳出循环的条件。
- 无环:表示为单向链表。
- 公共节点:但由于是单向链表的节点,每个节点只有一个next,因此从第一个公共节点开始,之后他们的所有节点都是重合的,不可能再出现分叉。
- c = a if a>b else b的扩展写法
a, b, c = 1, 2, 3
if a>b:
c = a
else:
c = b
- None 不在链表{1,2}中,
p2 = {1,2}
while None is not p2为真,则None is not p2。
def FindFirstCommonNode(self , pHead1 , pHead2 ):
p1,p2 = pHead1,pHead2
while p1 != p2:
p1 = p1.next if p1 else pHead2#if后面不要用pHead1,会陷入死循环,因为没有指向pHead1.next。
p2 = p2.next if p2 else pHead1
return p2
1. 4.反转链表
两个值互换:

迭代解法
总共初始化定义两个变量,总共有三个变量。
1. 5.链表中倒数第k个结点
- 在链表中的输出可以用 append,输出仍然是链表,输入用res=[]即可。
1. 6.链表中环的入口结点(双指针)
这类链表题目一般都是使用双指针法解决的,例如寻找距离尾部第K个节点、寻找环入口、寻找公共尾部入口等。
最容易想到的方法是遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
seen = set()
while pHead:
if pHead in seen:#遍历所有节点,每次遍历到一个节点时,判断该节点此前是否被访问过。
return pHead
else:
seen.add(pHead)
pHead = pHead.next
return None
set():表示一个集合,集合添加、删除
a = set('boy')
#集合添加
a.add('python')
#集合删除
a.update('python')
1. 7、删除排序链表中的重复元素
引入了一个新的概念,哑结点:是在处理与链表相关的操作时,设置在链表头之前的指向链表头的节点,用于简化与链表头相关的操作。
如果ListNode为{1,2,3,3,4,4,5}
dummy = ListNode(n)
输出为n
dummy = ListNode(pHead.val)
输出为链表对应的第一个节点。
1. 8、单链表的基本操作
#定义节点
class Node(object):
"""单链表的节点"""
def __init__(self,item):
self.item = item
self.next = None
class List(object):
"""单链表"""
def __init__(self):
self._head = None
def is_empty(self):
"""1、判断链表是否为空"""
return self._head is None
def length(self):
"""2、链表长度"""
cur = self._head
count = 0
while cur:
count += 1
cur = cur.next
return count
def items(self):
"""3、遍历链表"""
cur = self._head
if self.length() == 0:
return None
else:
for i in range(self.length()):
print(cur.item)
cur = cur.next
print('\n')
def add(self,item):
"""4、向头部添加元素"""
node = Node(item)
# 新结点指针指向原头部结点
node.next = self._head
# 头部结点指针修改为新结点
self._head = node
def append(self,item):
"""5、链表尾部添加元素"""
node = Node(item)
if self.is_empty():
self._head = node
else:
cur = self._head
while cur.next:
cur = cur.next
cur.next = node
if __name__ == "__main__":
link_list = List()
link_list.append(1)
link_list.append(2)
link_list.append(4)
link_list.append(8)
link_list.items()
2、队列剑指题目
2.1、用两个栈实现队列
-
为了实现队列的先进先出,用两个栈实现。先在第一个栈中进行全部元素压入;再将全部元素弹出到第二个栈中;实现先入先出。
例如:原始数组为1,2,3.进入第一个栈顺序为:1,2,3;第一个栈的出栈顺序为:3,2,1;进入第二个栈顺序为:3,2,1;第二个栈的出栈顺序为:1,2,3;
而在队列中:原始数组为1,2,3;进入队列顺序顺序为:1,2,3;出队列顺序为:1,2,3; -
要注意如果第二个栈不为空的话,要先将第二个栈的元素弹出。
-
注意第二个栈的的条件:当栈1为空;当栈2不为空;其它的话则直接弹出。
2.2、包含 min 函数的栈
数据栈 A : 栈 A 用于存储所有元素,保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
辅助栈B:栈 BB 中存储栈 AA 中所有 非严格降序 的元素,则栈 AA 中的最小元素始终对应栈 BB 的栈顶元素,即 min() 函数只需返回栈 BB 的栈顶元素即可。
-
push函数:重点为保持栈 BB 的元素是 非严格降序 的。
如果辅助栈B为空:x 压入栈 B。
如果辅助栈B的栈顶 > x:x 压入栈 B。
如果辅助栈B的栈顶 < x : 大于栈B的栈顶的数,无需再压入栈B,可以舍弃,将辅助栈B的栈顶在放入其中。因为要保证栈B的降序, -
POP函数:重点为保持栈 A,B 的 元素一致性 。
弹出栈 A,B栈顶元素 -
top函数:获取数据栈A栈顶元素
-
min函数:获取辅助栈B栈中最小元素
2.3、栈的压入、弹出序列
-
先遍历pushV,将pushV的元素按顺序放入到新栈stack中,直到stack 的栈顶元素 == 弹出序列元素 popped[i],开始执行while循环,出栈与 i++,直到stack的栈顶元素 != 弹出序列元素 popped[i] 。
-
再将pushV中的下一个元素放入到栈stack中,循环步骤1.
3、树
在树的实现中,一定考虑使用递归方法时,if语句,是用来表示递归结束的条件
3.1、二叉树的深度
3.2、二叉树的镜像
主要是将左右节点交换。
结束函数的执行,从函数返回:
return 与return None相同,返回值为None
3.2.1、递归三部曲
- 递归函数的参数和返回值
- 终止条件
- 单层递归的逻辑
3.3、二叉搜索树的第k个结点
- 二叉树(BST)中的每个节点X,它的左子树中所有项的值都小于X中的项,它的右子树中所有项的值大于X中的项。
BST 的中序遍历是升序序列。

- python中not 的具体用法
(1). not与 if 连用:代表not后面的表达式为False的时候,执行冒号后面的语句。
下面为最简单的例子:
a = False
if not a: (这里因为a是False,所以not a就是True)
print "hello"
这里就能够输出结果hello
代码中经常会有变量是否为None的判断,有三种主要的写法:
第一种是if x is None;是最好的写法,清晰,不会出现错误,以后坚持使用这种写法。
第二种是 if not x:;必须清楚x等于None, False, 空字符串"", 0, 空列表[], 空字典{}, 空元组()时对你的判断没有影响才行。
第三种是if not x is None(这句这样理解更清晰if not (x is None)) 。
在python中 None, False, 空字符串"", 0, 空列表[], 空字典{}, 空元组()都相当于False ,即:
not None == not False == not '' == not 0 == not [] == not {} == not ()
但是:
>>> x = 0
>>> y = None
>>> z = []
第一种写法的例子:
>>> x is None
False
>>> y is None
True
>>> z is None
False
第二种写法的例子:
>>> not x
True
>>> not y
True
>>> not z
True
第三种写法的例子:
>>> not x is None
True
>>> not y is None
False
>>> not z is None
True
(2).判断元素是否在列表或者字典中:如果a不在列表b中,那么就执行冒号后面的语句
a = 5
b = [1, 2, 3]
if a not in b:
print "hello"
- 本题代码
def KthNode(self, pRoot, k):
# write code here
#这里的k == 0,可以替换为not k。因为只要k为0,not k返回值为True。
if not pRoot or k == 0:
return
res = []
def Traversal(node):
#这里的node is None,可以替换为not node。因为只要node为None,node is None返回值为True。
if len(res) >= k or node is None:
return
Traversal(node.left)
res.append(node)
Traversal(node.right)
Traversal(pRoot)
if len(res) < k:
return
return res[k-1]
3.4、平衡二叉树
3.4.1、平衡树概念
平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
注:我们约定空树是平衡二叉树。
3.4.2、计算任意节点的高度:
此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1 。
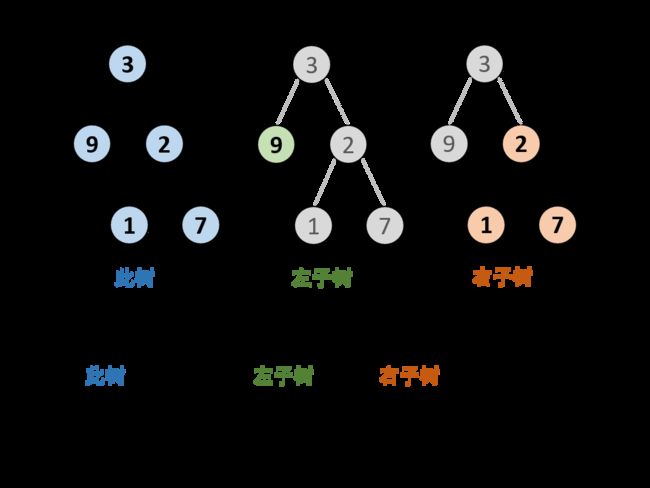
3.4.3、python函数调用
(1)、在类中一个函数调用另一个函数:只要在那个被调用的函数前加self即可
class Fun(object): #定义类
def __init__(self,x): #初始化参数
self.x = x
def fun1(self,y): #定义第一个函数,self表示继承上面的参数x,而y是fun1自己的一个参数,不是类的参数
a = y**2+2+self.x
return a
def fun2(self): #定义第二个函数
b = self.fun1(3)+3 #调用fun1,同时参数y实例化为3
return b
def fun3(self):
return(self.fun1(3)+3) #便捷的输出,不想再定义一个参数来储存
ans = Fun(1) #实例化,参数x实例化为1,但参数y是没有实例化的,因为y是fun1自己的参数
ans1 = ans.fun1(2) #将参数y赋值为2
ans2 = ans.fun2() #要有括号
ans3 = ans.fun3()
print(ans1,ans2,ans3)
>>>>> 7 15 15 #结果
(2)、在类外,直接调用即可。嵌套函数也是直接调用。
def test1():
print("*" * 50)
def test2():
print("-" * 50)
# 函数的潜逃调用
test1()
test2()
3.4.3、每一个函数必须满足的条件
class Solution:
def high(self,root):
if root == None:#递归结束的条件
return 0
return max(self.high(root.left), self.high(root.right))+1
def IsBalanced_Solution(self, pRoot):
if pRoot == None:
return True
if not self.IsBalanced_Solution(pRoot.left):#先序遍历递归,判断 当前子树的左子树 是否是平衡树
return False
if not self.IsBalanced_Solution(pRoot.right):#先序遍历递归,判断 当前子树的右子树 是否是平衡树;
return False
isbalance = self.high(pRoot.left) - self.high(pRoot.right)
if abs(isbalance) <= 1:
return True
return False
3.5、按之字形顺序打印二叉树
算法流程:
1、特例处理: 当树的根节点为空,则直接返回空列表 [] ;
2、初始化: 打印结果空列表 res ,包含根节点的双端队列 deque ;
3、BFS 循环: 当 queue 为空时跳出;
(1)、新建列表 tmp ,用于临时存储当前层打印结果;
(2)、当前层打印循环: 循环次数为当前层节点数(即 queue 长度);
A. 出队: 队首元素出队,记为 node;
B. 添加子节点: 若 node 的左(右)子节点不为空,则加入 deque ;
(3)、打印: 若之前的res长度为奇数(即本层为偶数层),将tmp倒序插入; 否则,tmp正序插入;
4、返回值: 返回打印结果列表 res 即可;
class Solution:
def Print(self, pRoot):
# write code here
if not pRoot:
return []
queue = [pRoot]#这里插入的是树的根节点,而不是整棵树。
res = []
#这里的while循环是用来判断树的层数是否已经没有了。在最后一层的下一层则跳出循环。
while queue:
tmp = []
#len(queue)表示的是每一层节点的长度,而不是整个树的层数。用for来遍历
for _ in range(len(queue)):
#queue.pop(0)保证每次的queue都只包含该层节点,而非所有层的节点。
cur_node = queue.pop(0)
tmp.append(cur_node.val)
if cur_node.left:
queue.append(cur_node.left)
if cur_node.right:
queue.append(cur_node.right)
if len(res)%2 == 1:
res.append(tmp[::-1])
else:
res.append(tmp)
return res
3.6、把二叉树打印成多行
3.6.1、打印二叉树的算法过程
- 判断树是否为空树,若是空树则输出为[]
3.7、二叉树的下一个结点
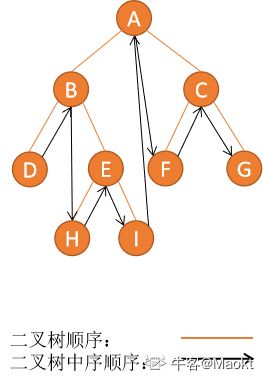
仔细观察,可以把中序(DBHEIAFCG)下一结点归为几种类型:
1、有右子树,下一结点是右子树中的最左结点,例如 B,下一结点是 H
2、无右子树,且结点是该结点父结点的左子树,则下一结点是该结点的父结点,例如 H,下一结点是 E
3、无右子树,且结点是该结点父结点的右子树,则一直沿着父结点追朔,直到找到某个结点是其父结点的左子树,如果存在这样的结点,那么这个结点的父结点就是我们要找的下一结点。例如 I,下一结点是 A;例如 G,并没有符合情况的结点,所以 G 没有下一结点
class Solution:
def GetNext(self, pNode):
# write code here
if not pNode:
return None
#pNode是一个节点,而不是一棵树。
#如果有右子树,则找右子树中最左的子节点
if pNode.right != None:#单纯的if pNode.right无法运行,得加上!= None。
res = pNode.right
while res.left != None:
res = res.left
return res
#无右子树,则向上找第一个是其父节点的左节点的点,这个父节点就是遍历序列中的下一个节点
while pNode.next:#pNode.next表示该节点的父节点
#判断该节点是父节点的左子树还是右子树,即该节点的父节点的左子树是否等于该节点。
if pNode.next.left == pNode:
return pNode.next
pNode = pNode.next #沿着父节点向上遍历
return #到了根节点仍没找到,则返回空
3.8、重建二叉树
3.8.1、重建二叉树过程分析
- 前序遍历中的第一个节点就是总的根节点。前序遍历的首元素 为 树的根节点 node 的值
- 中序遍历作用:定位到了根节点,那么我们就可以分别知道左子树和右子树中的节点数目。在中序遍历中搜索根节点 node 的索引 ,可将 中序遍历 划分为 [ 左子树 | 根节点 | 右子树 ] 。
- 根据中序遍历中的左 / 右子树的节点数量,可将 前序遍历 划分为 [ 根节点 | 左子树 | 右子树 ] 。
- 再根据前序遍历划分出的 [ 根节点 | 左子树 | 右子树 ] 可以知道左右字数的根节点。
- 再循环上面几步,就可以分子树的左右子树。得到完整的二叉树。
3.8.2、重建二叉树算法解析
为什么先开启左子树递归而非右子树:因为无论是中序遍历还是前序遍历都是左子树在前,右子树在后。
str.index(str, beg=0, end=len(string))
str -- 指定检索的字符串
beg -- 开始索引,默认为0。
end -- 结束索引,默认为字符串的长度
4、递归、动态规划
4.0、动态规划初始化的方法
- 对于整数的动态规划
f = [0]+[1]*number
f[i] = 2*f[i-1]
- 数组的动态规划
dp = [0]*(len(array))
dp[0] = array[0]
dp[i] = max(dp[i-1]+array[i],array[i])
4.1、斐波那契数列
可以采用递归,但是可能会因为计算量过大,超时。
- 斐波拉契数列的定义(即 f(n)=f(n-1)+f(n−2))
class Solution:
def Fibonacci(self, n):
# write code here
if n <= 1:
return n
a,b = 0,1
s = 0
for i in range(2,n+1):
**#下面这三行代码交换,可以用a, b = b, a + b,这也是状态转移方程**
s = a+b
a = b
b = s
return s
- 下面这个代码,循环的第一次:_为0时,c的结果表示f(1)的值,所以最终返回f(n)的值,应该是a而不是b。
def Fibonacci(self, n):
# write code here
a,b = 0,1
for _ in range(n):#当n=0时,循环不执行,直接输出a=0.
c= a+b #下面三行代码也可以表示为:a,b = b,a+b
a = b
b = c
return a
4.2、跳台阶(斐波那契数列)
主要采用逆向思维的方法:如果我从第n个台阶进行下台阶,下一步有2中可能,一种走到第n-1个台阶,一种是走到第n-2个台阶。所以f[n] = f[n-1] + f[n-2].
不知道范围的时候,可以从用以下方法找出循环的范围:
a0 = 1,b0 = 1,→ f(1) = 1
a1 = 1,b1 = 2,→ f(2) = 2
所以用b作为返回值,且n比a,b对应的值要大1 ,所以循环取(0,n-1)
4.3、跳台阶扩展问题
此题主要是找出n与n-1的关系,f[n-1] = f[n-2] + f[n-3] + … + f[0],优化可得f[n] = 2*f[n-1]。
动态规划初始化:
def jumpFloorII(self, number):
# write code here
f = [0]+[1]*number
for i in range(2,number+1):
f[i] = 2*f[i-1]
return f[number]
4.4、矩形覆盖(类似斐波那契数列)
主要是找到前后关系,一般来说,写出前四个f(n)就可以得到关系:f[n] = f[n-1] + f[n-2]
5、计算数字出现次数、重复之类的
5.1、数组中出现次数超过一半的数字
- 除法/和//的区别
//:取整除 - 返回商的整数部分(向下取整),例如:6 / 4 =1.5,int(7.2/2)=3
/:除 - x除以y。例如:6 // 4 = 1,得到的结果是整数。
- numbers.count(i)函数,可以计算 i 在 numbers 出现的次数。
6、数组
6.1、扑克牌顺子
算法思路:
- 排序;
- 用count找出0的个数n;
- 遍历数组,遍历区间为[n,4];
- 计算出排序后两个相邻数的累计和 count += (numbers[i+1]-numbers[i]-1);
- 如果累计和为0(count为0表示排序后相邻两个数为连续的自然数); 或者累计和不为0时,和为几,表示需要插入的0的个数为几,才能返回真。
6.2、构建乘积数组
初始化数组的长度:B = [1]*28,则数组的长度为28,每个元素的值都为1。
- 不能使用除法 ,即需要 只用乘法 ,因为可能会出现A[i]=0,如果len(A)=n+1
- 计算下三角的各元素的乘积,从 B[1]——B[n] 开始才有下三角,此时索引区间为(1,len(A))
- 计算上三角的个元素的乘积,B[0]——B[n-1]才有上三角,此时索引的区间为(0,len(A)-1)但是计算过程中需要i+1,所以变为(0,len(A)-2 )。
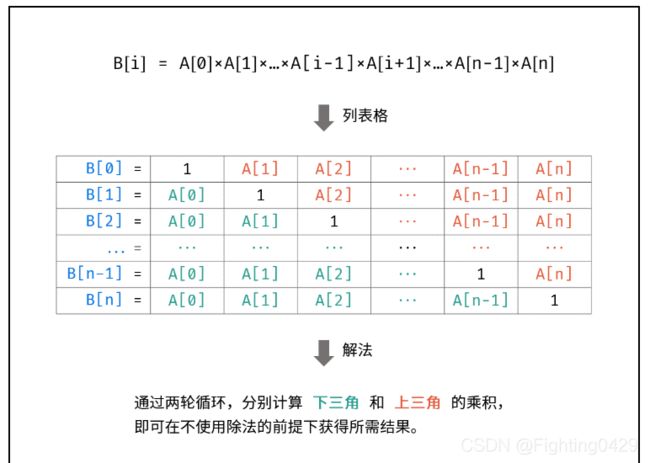
class Solution:
def multiply(self, A):
# write code here
l = len(A)
B,tmp = [1]*l,1
if l <= 1:
return None
for i in range(1,l):
B[i] = B[i-1] * A[i-1]#计算上三角
for i in range(l-2,-1,-1):#逆序输出索引:l-2,l-3,...,0.
tmp = tmp*A[i+1]#计算下三角,从下往上计算
B[i] = B[i]*tmp#逆序输出B的值,
return B
6.3、二维数组中的查找
6.3.1、按行查找
- array[i][-1]表示是某行的倒数第一个数。
- 对于数组一定判断数组长度是否为0.
6.4、旋转数组的最小数字
-
数组是 numpy 中的,求解数组的行和列:行:len(b) ,b.shape返回的是行和列,b.size返回的是总长度。
-
求解List的长和宽:使用的函数为len(a),len(a[0])
-
注意数组本身已经是旋转数组了,这个原始数组是递增的。
6.4.1、二分查找
6.5、顺时针打印矩阵
7、计算和
7.1、和为S的连续正数序列
7.1.1、滑动窗口法
滑动窗口的性质:
- 为了编程方便,滑动窗口一般表示为左闭右开区间。在一开始,i=1, j=1i=1,j=1,滑动窗口位于序列的最左侧,窗口大小为零。
- 窗口的左边界和右边界永远只能向右移动,而不能向左移动。
滑动窗口需要解决的难题:
-
窗口何时扩大,何时缩小?(左右边界的移动条件)
当窗口的和小于 target 的时候,窗口的和需要增加,所以要扩大窗口,窗口的右边界向右移动;
当窗口的和大于 target 的时候,窗口的和需要减少,所以要缩小窗口,窗口的左边界向右移动;
当窗口的和恰好等于 target 的时候,我们需要记录此时的结果。设此时的窗口为 [i, j)[i,j),那么我们已经找到了一个 ii 开头的序列,也是唯一一个 ii 开头的序列,接下来需要找 i+1i+1 开头的序列,所以窗口的左边界要向右移动。 -
滑动窗口能找到全部的解吗
7.1.2、算法步骤
- 建立滑动窗口的初始左右边界。
- 循环终止条件,为左边界的值 > 目标值的一半。(因为这是递增整数序列,若左边界的值 > 目标值的一半,那么右边界的值一定大于目标值的一半。)
- 左右边界的移动。先移动右窗口,再移动左窗口,找出符合目标值的移动窗口。
- 记录结果。列出某左闭右开区间内所有值:arr = list(range(i, j))
- 进行下一次移动,左边界右移
7.2、和为S的两个数字(递增排序的数组)
输出的两个数字不一定是连续的,所以不能用滑动窗口来解决。
7.2.1、双指针法
1.初始化:指针i指向数组首, 指针j指向数组尾部
2. 如果arr[i] + arr[j] == sum , 说明是可能解。
通过下列代码,找出最小值。
min_ = float('inf')#表示无穷大,最小值的初始化可以为无穷大。最大值的初始化可设置为0.
if array[i] * array[j] < min_:
res = [array[i] , array[j]]
min_ = array[i] * array[j]
- 否则如果arr[i] + arr[j] > sum, 说明和太大,所以–j
- 否则如果arr[i] + arr[j] < sum, 说明和太小,所以++i
7.3、连续子数组的最大和
7.3.1、动态规划解法一
力扣题解动态规划具体步骤
- 状态定义: 设动态规划列表 dp ,dp[i] 代表以元素 nums[i]为结尾的连续子数组最大和。
- 转移方程: 要看的就是这个数前面的部分要不要加上去。大于零就加,小于零就舍弃。这样的话可以保证连续子数组的值的最大和。
- 初始状态: dp[0] = nums[0],即以 nums[0] 结尾的连续子数组最大和为 nums[0] 。
- 返回值: 返回 dp 列表中的最大值,代表全局最大值。
class Solution:
def FindGreatestSumOfSubArray(self, array):
# write code here
for i in range(1,len(array)):
array[i] = array[i] + max(array[i-1],0)#每循环替换一次,array[i] 中的值就会被替换,已经是某个连续子数组的和了。
return max(array) # max(array)可以找出连续子数组的最大和
7.3.2、动态规划解法二
动态规划的定义:dp = [0]*(len(array))
dp[0] = array[0]
dp[i] = max(array[i],array[i]+dp[i-1]),主要是用来判断dp[i-1]的值是否为正,如果为负的话,舍弃之前的序列和,重新开始。
def FindGreatestSumOfSubArray(self, array):
# write code here
dp = [0]*(len(array))
dp[0] = array[0]
res = []
for i in range(1,len(array)):
dp[i] = max(dp[i-1]+array[i],array[i])
return max(dp)
8、数学
8.1、数值的整数次方
8.1.1、逻辑操作
-
与操作(&):两位同时为“1”,结果才为“1”,否则为0
-
或运算符(|):参加运算的两个对象只要有一个为1,其值为1。
-
异或运算符(^):参加运算的两个对象,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
运算规则:0^ 0=0; 0 ^ 1=1; 1^ 0=1; 1^1=0; -
取反运算符(~):对一个二进制数按位取反,即将0变1,1变0。
-
左移运算符(<<):将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)
例:a = a << 2 将a的二进制位左移2位,右补0;

-
右移运算符(>>):将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
127的补码:0111 1111 右移一位: 0011 1111 右移二位: 0001 1111
-128的补码:1000 0000 右移一位: 1100 0000 右移二位: 1110 0000 -
向下整除 n // 2等价于 右移一位 n >> 1 ;
取余数 n%2 等价于 判断二进制最右一位值 n&1 ;可以判断是奇数还是偶数。n&1为真 等价于 n%2==1,为奇数。
8.1.2、快速幂解析(二分法角度):
不管是n是奇数还是偶数,倒数第一轮n的值都会变成0,跳出循环。
那么倒数第二轮的值,都会是1,会将x的偶数的最终幂结果转化到res中去。


- 当 x = 0 时:直接返回 0 (避免后续 x = 1 / x 操作报错)。
- 初始化 res = 1 ;
- 当 n < 0 时:把问题转化至 n≥0 的范围内,即执行 x = 1/x ,n = - n ;
- 循环计算:当 n = 0 时跳出;(通过n&1来判断n是奇数还是偶数)

- 返回 res。
8.2、不用加减乘除做加法(没搞懂)
两数字的二进制形式a,b,其和s = a+b。
通过下图可知,进位与无进位不可能同时出现同为1的情况:
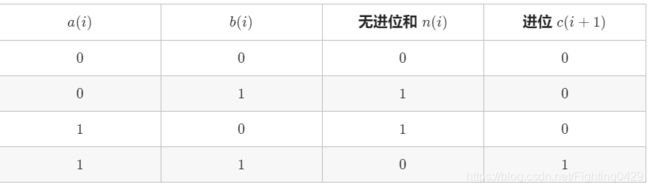
无进位和 n 与进位 c 的计算公式如下:

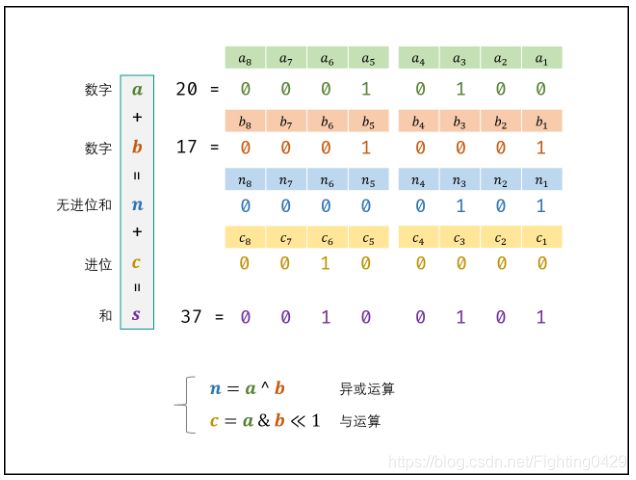
class Solution:
def add(self, a: int, b: int) -> int:
x = 0xffffffff
a, b = a & x, b & x
while b != 0:
a, b = (a ^ b), (a & b) << 1 & x
return a if a <= 0x7fffffff else ~(a ^ x)
8.3、丑数
-
定义数组 dp,其中 dp[i] 表示第 i 个丑数,第 n 个丑数即为 dp[n] 。由于最小的丑数是 11,因此 dp[1]=1。
-
定义三个指针 p2,p3,p5,初始值都为1。
-
通过三个指针,得到下一个丑数,即找出 1 与 2,3,5 相城的最小值,dp[i] = min( dp[p2] * 2, dp[p3] * 3, dp[p5] * 5 ),然后分别比较 dp[i] 与 dp[p2] * 2, dp[p3] * 3, dp[p5] * 5 中哪个相等,如果相等则将对应的指针加 1。 例如:p2+1=2,则在下一次循环中可以得到dp[p2] * 2,即dp[2] * 2,以此循环可以保证每一个丑数都有一次机会与2相乘,一次机会与3相乘,一次机会与5相乘。并且可以保证不同丑数乘以2,3,5时的比较结果。
-
重复循环2—n次。
三个指针的使用:首先三个指针 dp[p2]、dp[p3]、dp[p5] 都指向1,乘以2,3,5之后得到2,3,5。
pointer2, 指向1, 2, 3, 4, 5, 6中,还没使用乘2机会的丑数的位置。该指针的前一位已经使用完了乘以2的机会。
pointer3, 指向1, 2, 3, 4, 5, 6中,还没使用乘3机会的丑数的位置。该指针的前一位已经使用完了乘以3的机会。
pointer5, 指向1, 2, 3, 4, 5, 6中,还没使用乘5机会的丑数的位置。该指针的前一位已经使用完了乘以5的机会。
if not index:
return 0 #需要返回0的时候,return后面一定不能为空。
dp = [1]*index#对于动态规划的定义方法。
p2=p3=p5=0
for i in range(1,index):
n2,n3,n5 = dp[p2]*2,dp[p3]*3,dp[p5]*5
dp[i] = min(n2,n3,n5)
if dp[i] == n2:
p2 += 1
if dp[i] == n3:
p3 += 1
if dp[i] == n5:
p5 += 1
return dp[index-1]
8.4、二进制中1的个数
8.4.1、逐位判断
8.4.2、python中负数补码运行
-
32位二进制数就是有32个0或者1:全1表示为x = 0xffffffff。
-
正数的补码还是其本身;负数的补码是其反码+1。
-
Python 中的整型也是用 补码形式存储的,正数和负数都是。
-
Python 中 bin 一个正数(十进制表示)结果就是它的二进制补码表示形式;但是Python 中 bin 一个负数(十进制表示),输出的是它的原码的二进制表示加上个负号。
-
正负数补码计算方法:
负数补码计算:
x = 0xffffffff
n = x&n
n = bin(n)
正数补码计算:
n = bin(n)
9、字符串
9.1、字符流中第一个不重复的字符
9.1.1、python基础知识
-
not c in dic 整体返回一个布尔值,表示如果c 不在 dic 中,则返回 False 。c in dic 表示如果c 在 dic 中,则返回 True。这两者表示的情况刚好相反。
9.1.2、题目分析
-
字符流:表示源源不断的向池子中添加字符,而不是一次性将整个字符全部添加完成。
-
输入字符流为"google"时,表示先输入“g→‘go’→“goo”→goog…→"google",对应题目中,如果只出现一次,则返回第一个只出现一次的字符;如果当前字符流没有存在出现一次的字符,返回#字符。则前面字符串对应返回的字符为:“g→‘gg’→“ggg”→ggg#…→"ggg#ll"
-
Insert函数表示遍历字符串,FirstAppearingOnce作用是找出第一个不重复的字符。
-
算法流程:
①、遍历输入字符串,将遍历结果放入新的字符串和字典中
②、字典的键为字符,值为字符出现的次数。(如果重复出现则值加1)
③、用新字符串中的字符对应字典中的键,循环遍历的返回值为第一次只出现一次的字符(比如‘go’,返回值为’gg’,因为第一个不重复的字符为g,所以后面返回的也全为g)。
④、否则,遍历完之后,没有只出现一次的字符,则返回#。
9.2、替换空格
python 的内置函数:s = s.replace(" “,”%20") :用空格替换 %20
9.3、第一个只出现一次的字符
for 循环使用 enumerate:前面的元素表示索引,后面的数字表示元素。

9.4、字符串的排列
9.4.1、python基础知识
Python中有join()和os.path.join()两个函数,具体作用如下:
-
join()函数 。语法: ‘sep’.join(seq);上面的语法即:以sep作为分隔符,将seq所有的元素合并成一个新的字符串
返回值:返回一个以分隔符sep连接各个元素后生成的字符串。 -
os.path.join()函数;语法: os.path.join(path1[,path2[,…]])
返回值:将多个路径组合后返回
9.4.2、
9.5、左旋转字符串
def LeftRotateString(self, s, n):
# write code here
if n > len(s):
return s
s1 = s[n:]#表示从n到最后那个数。
s2 = s[:n]#表示索引值从0到n-1.
return s1+s2
9.6、把字符串转换成整数
9.6.1、算法流程
- 删除首尾空格(字符串为空则直接返回)
- 判断首位符号(保存负号,若无符号位,则需从 i = 0 开始数字拼接)
- 遇到非数字的字符则跳出。
- 最后进行数字拼接。res=10×res+x
9.7、表示数值的字符串
9.7.1、有限状态自动机
字符类型:
空格 「 」、数字「 0—9 」 、正负号 「 ± 」 、小数点 「 .」 、幂符号 「 eE 」
状态定义:
按照字符串从左到右的顺序,定义以下 9 种状态。
- 开始的空格
- 幂符号前的正负号
- 小数点前的数字
- 小数点、小数点后的数字
- 当小数点前为空格时,小数点、小数点后的数字
- 幂符号
- 幂符号后的正负号
- 幂符号后的数字
- 结尾的空格
合法的结束状态有 2, 3, 7, 8

10、孩子们的游戏(圆圈中最后剩下的数)
-
f(n, m),表示长度为n的序列,删除n-1次,最后留下元素的序号;则f(n-1, m)表示长度为n-1的序列,删除n-2次,最后留下元素的序号;…;则 f(1, m) = 0。(其中最后留下元素的序号都表示删除元素后,新序列中的下标,而不是长度为n的序列中,对应的初始下标,本题要求的是初始下标对应的值)
-
长度为n的序列,第1次删除,划掉了下标为(m-1)%n的数字,剩下n-1个数;下一次开始的下标为 m % n。
-
假设 x = f(n - 1, m),表示长度为n-1时,最终留下的元素的序号为x(此时的x是第一次删除后n-1个序列中,新的排序的下标,新排序第一个数为 m % n 开始)。
-
x = f(n - 1, m)也表示从 m % n 开始往后数 x 个数,即 m % n + x,在初始序列中的下标为 f(n, m) = (m % n + x) % n = (m + x) % n
11、排序
11.0、排序算法的稳定性
11.1、快速排序
快排的原理:在数组中任意选择一个数字作为基准,用数组的数据和基准数据进行比较,比基准数字大的数字的基准数字的右边,比基准数字小的数字在基准数字的左边。时间复杂度O(nlogn)
def fast_sort(num):
if len(num)<=1:
return num
else:
left,right = [],[]
base = num[len(num)//2]
num.remove(base)
for i in num:
if i<= base:
left.append(i)
else:
right.append(i)
return fast_sort(left)+[base]+fast_sort(right)
num = [2,4,8,7,6,5]
print(fast_sort(num))
11.2、冒泡排序
冒泡排序重复地走访需要排序的元素列表,依次比较两个相邻的元素,如果顺序(如从大到小或从小到大)错误就交换它们的位置。重复地进行直到没有相邻的元素需要交换,则元素列表排序完成。冒泡排序总的平均时间复杂度为:O(n2)
def _sort(num):
for i in range(len(num)-1):
for j in range(len(num)-1-i):
if num[j] > num[j+1]:
num[j],num[j+1] = num[j+1],num[j]
return num
num = [2,4,8,7,6,5]
print(_sort(num))
**改进版:**上述代码中加入了一个标志位 isSorted ,利用布尔变量 isSorted 作为标记。如果在本轮排序中,元素有交换,则说明数列无序;如果没有元素交换,说明数列已然有序,直接跳出大循环。
在基础版中已经知道就算当前数列中的某几个元素之间是有序的(如最后的4、5),元素遍历依然会执行。而我们改进版就是为了解决这个问题。
def _sort(num):
for i in range(len(num)-1):
isSorted = True
for j in range(len(num)-1-i):
if num[j] > num[j+1]:
num[j],num[j+1] = num[j+1],num[j]
isSorted = False
if isSorted:
break
return num
num = [2,4,8,7,6,5]
print(_sort(num))
11.3、归并排序
- 将一个序列从中间位置分成两个序列;
- 在将这两个子序列按照第一步继续二分下去;
- 直到所有子序列的长度都为1,也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。
复杂度为O(nlog^n)
def marge(list):
n = len(list)
if n<=1:
return list
mid = n//2
#left采用归并排序之后,形成有序的新列表
left = marge(list[:mid])
# right采用归并排序之后,形成有序的新列表
right = marge(list[mid:])
#将两个有序的子序列合并为一个新的整体
#排序形成的新数组,是之前拆分开的数组之间的排序。
left_p,right_p = 0,0
res = []
while left_p < len(left) and right_p < len(right):
if left[left_p] < right[right_p]:
res.append(left[left_p])
left_p += 1
else:
res.append(right[right_p])
right_p += 1
res += left[left_p:]
res += right[right_p:]
return res
num = [2,4,8,7,6,5]
print(marge(num))
11.4、插入排序
插入排序是将元素列表中未排序的数据依次插入到有序序列中。从元素列表的第一个数据开始(将第一个数据视为已排序序列),按顺序将后面未排序的数据依次插入到前面已排序的序列中。对每一个未排序数据进行插入,是将该数据依次与相邻的前一个数据进行比较,如果顺序错误则交换位置,直到不需要交换则该数据插入完成。
# coding=utf-8
def insertion_sort(array):
for i in range(len(array)):
cur_index = i
#未排序的第一个数据与已排序的最后一个数据进行比较。cur_index - 1 >= 0表示插入的数据已经通过交换位置到达了数列的最前端
while array[cur_index - 1] > array[cur_index] and cur_index - 1 >= 0:
array[cur_index],array[cur_index - 1] = array[cur_index - 1],array[cur_index]
cur_index -= 1
return array
if __name__ == '__main__':
array = [10,17,50,7,30,24,27,45,15,5,36,21]
print(insertion_sort(array))