python每日算法 | 图文+“农村包围城市”详解堆排序，手把手学会

  创作不易，来了的客官点点关注，收藏，订阅一键三连❤    

---

前言

程序=数据结构+算法，算法是数学理论和工程实现的杂糅，是一个十分有趣神奇的学问。搞懂算法用另一种视角看编程，又会是一种全新的感受，如果你也在学习算法，不妨跟主任萌新超差一起学习，拿下算法！

---

系列文章目录

python每日算法 | 图文结合详解快速排序，手撕快排代码！

python每日算法 | 图文挑战十大排序算法DAY1，再也不用担心面试官问冒泡、选择、插入排序！

python每日算法 | 实现四大查找算法，生动形象，保证一看就会！

---

概述

本期的内容将介绍十大排序算法之堆排序，通过本期内容你不仅能知道代码堆排序如何用python实现，还将学会使用堆排序模块以及用堆排序解决topk问题等等！再也不用担心面试官问堆排序是什么啦！ 

---

目录

前言

系列文章目录

概述

超超python每日算法思维导图

堆排序

了解树

关于树的⼀些概念

了解二叉树

什么是堆

堆的向下调整性质

堆的构造

  堆排序的过程

实现堆排序的算法

python中堆排序的内置模块

堆排序时间复杂度

堆排序解决topk问题

十大排序之五大排序总结

---

超超python每日算法思维导图

堆排序

了解树

树是一种可以递归定义的数据结构，树结构是递归定义的，树是由n个节点组成的集合：

如果n=0，那这是⼀一棵空树；

如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树。

关于树的⼀些概念

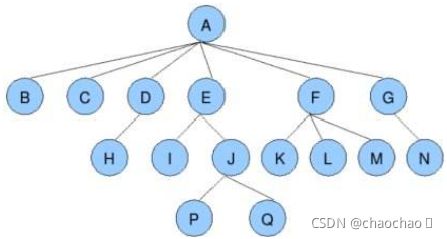
根节点：一棵树中，没有双亲结点的结点，例如图中的A

节点的度：一个节点含有的子树的个数称为该节点的度，例如D节点的度为1（H），E节点的度为2（I，J）

树的度：一棵树中，最大的节点的度称为树的度，例如图片中树的度为A节点的6

树的高度或深度：树中节点的最大层次，图片的高度位4

叶子节点或终端节点：度为0的节点称为叶节点；即不能分叉的点，例如B、C、H、I、P等

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点，E是I的父节点

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点，I是E的孩子节点

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推

森林：由m（m>=0）棵互不相交的树的集合称为森林

了解二叉树

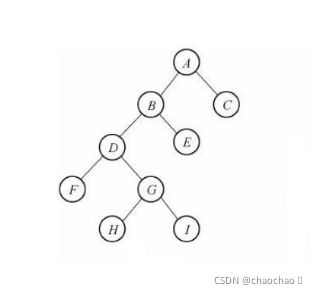
 二叉树：度不超过2的树，每个节点最多有两个孩子节点，两个孩子节点被区分为左孩子节点和右孩子节点

满二叉树与完全二叉树

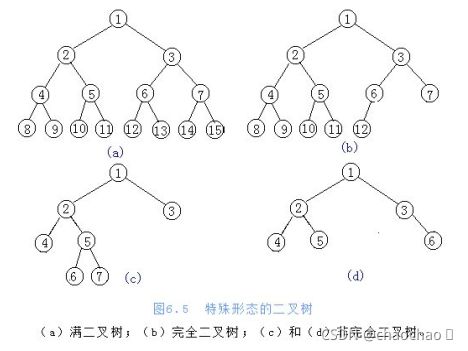
 满二叉树：⼀个⼆叉树，如果每一个层的结点数都达到最⼤大值，则这个二叉树就是满二叉树。

完全二叉树：叶节点只能出现在最下层和次下层，并且最下⾯面一层的结点都集中在该层最左边的若⼲干位置的二叉树

二叉树的存储方式

链式存储方式（后续算法了解）

顺序查找方式：

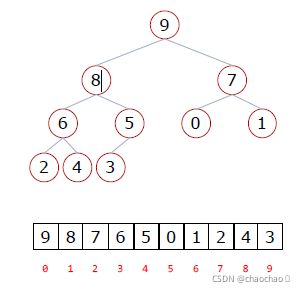
  从图片中，我们发现：

父节点和左孩子节点的编号下标有什关系？

0-1 1-3 2-5 3-7 4-9（列表中的下标）

i → 2i+1

父节点和右孩子节点的编号下标有什么关系？

0-2 1-4 2-6 3-8 4-10（对应列表中的下标）

i → 2i+2

因此得到以下规律：

已知双亲的下标，则左孩子的下标为：Left=2parent+1，则右孩子的下标为：Right=2parent+2；

已知孩子结点（不区分左右）的下标，则双亲的下标为：（child-1）//2

什么是堆

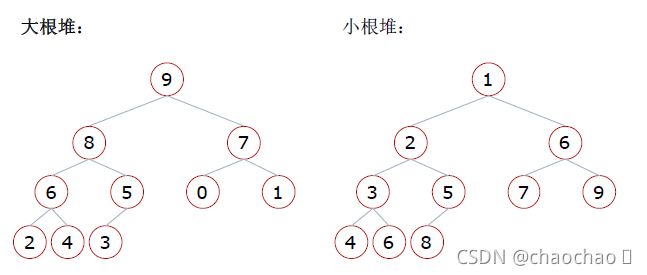
堆：堆是一种特殊的完全二叉树结构，分为大根堆和小根堆

大根堆：一棵完全⼆叉树，满足任一节点都比其孩子节点大

小根堆：一棵完全⼆叉树，满足任一节点都比其孩子节点小

堆的向下调整性质

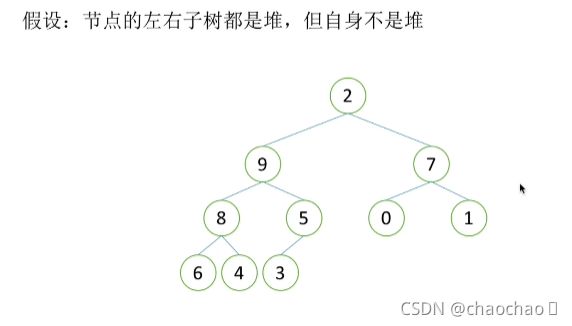
假设根节点的左右子树都是堆，但根节点不满足堆的性质，可以通过一次向下的调整来将其变成一个堆。

以上图片展示的是节点的左右字数都是堆，但是自身不是的情况 ，也是堆排序向下调整性质的前提。

 接下来就开始向下调整，我们将第一层看作是“省长”，第二层代表“市长”，第三层代表“县长”，第四层代表“村长”，数值越大代表能力越强，群众更拥护，才能选上对于层的“长”。

此时我们就看“2”，他不能当省长，因为““9”和“7”都比它强，那么强者胜。我们就将“9”放上去；

那么“2”能当市长吗?不能，因为“8”和“5”都比他厉害，因此强者胜“8”上去，以此类推，最后“2”就只能当“村长”，选举完成，那么此时大根堆也完成了，以上就是向下调整的性质。（当然如果最上面的是“6”而不是“2”，那么它的位置就在县长以上，意思是向下调整不一定都是去的最下一层）

 因此我们总结，堆化（向下调整）或者向上调整的前提都是：在二叉树中，只有一个位置不满足堆的性质，其它位置都满足堆的性质。

向下调整是让调整的结点与其孩子节点进行比较，向上调整是让调整的结点与其父亲结点进行比较。

那么堆如如何构造的呢？

堆的构造

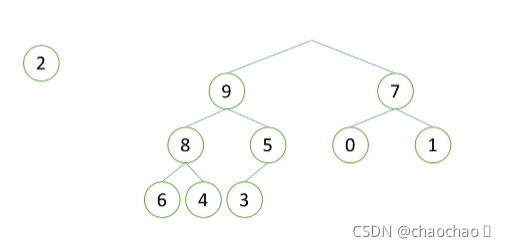
如图是一个无序的堆，我们从上述堆的向下性质能够得出，要实现堆的向下性质，就要保证省长之下的“市长”是称值的，然后才能选“省长”上去.....如果两个县要有序，就需要两个村有序，那么就是需要一个合格的“村长”，这也是我们理解构造堆的“农村包围城市”思想。

那么转为专业术语，我们就要从最后的非叶子节点来看。

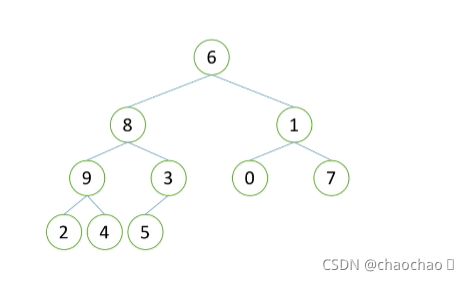
首先我们看是否“村长”需要向上调整，即图片中的“5”，因为“5”>"3",因此“5”就由村长变为“县长”，同时他也上不去了；接下来就看“4”、“2”它们都已经合规了，不要调整，“村长”就调整了；

那么接下来看上一层“县长”是否需要向上调整了，从“7”开始，明细它来当“市长”；接下来依次看“0”、“3”，他们都符合规则，不用进行调整，接着看“9”，明显它一个往上调整当“市长”，“8”就下来当“县长”，“县长“就调整完了；

接下来就看“市长”是否需要向上调整，从“7”开始，我们发现“7”比“6”大，因此“7”调整“为“省长”；再看“9”，“9”>“7”，那么“9”选为“省长”，那么“市长”也调整完了，此时“农村包围城市”完成，我们也完成了堆的构建。

  堆排序的过程

 堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

堆排序步骤：

1.建立堆：可以理解为农村包围城市选村长，从叶子节点开始，往上调整，数值大的上去，数值下的换下来）

2.得到堆顶元素，为最大元素

3.去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序

4.堆顶元素为第⼆大元素

5.重复步骤3，直到堆变空

实现堆排序的算法

我们以大根堆为例，因为大根堆排序出来的结果是升序。

# 向下调整函数

def shift(lst,low,high):  # low:对根节点的位置；high:堆最后一个元素的位置

    i = low  # 标记low

    j = 2 * i + 1  # j代表左孩子位置

    tmp = lst[low]  # 把堆暂时顶存起来

    while j <= high:  # 只要j位置大于high就说明没有元素了，循环就停止，所欲j<=high时就代表有元素，就循环

        if j + 1 <= high and lst[j+1] > lst[j]:  # 首先判断是否j这一层有右孩子(j + 1直的j这一层的另一个数)，其次判断j这一层元素的大小,j+1(右孩子)大于j（左孩子），则j指向j+1

            j = j + 1 # j指向右孩子

        if lst[j] > tmp:  # 然后判断j和堆顶的元素（tmp）的大小，如果j位置的元素大于堆顶元素，则堆顶元素和j（左孩子）位置互换

            lst[i] = lst[j]

            i = j  # low堆顶的位置指向i，继续看下一层

            j = 2 * i + 1 # 同时j指向下一层的左孩子

        else:  # tmp最大，则把tmp放到i的位置上

            lst[i] = tmp  # 把tmp放到某一级

            break

    else:

        lst[i] = tmp  # 把tmp放到叶子节点上

 

# 堆排序主函数

def heap_sort(lst):

    n = len(lst) # 获取列表长度

    # 先建堆

    for i in range((n-2)//2,-1,-1):  #从最后一个根节点，到最上面的根节点  

    # i代表建堆时调整部分的根的下标，（n-2）//2是根到位置，n-1是孩子节点下标，(n-1-1)//2代表根节点的下标，-1是最后的根节点位置（0），那么range就是-1

        shift(lst,i,n-1)  # i为堆顶，high为最后一个节点n-1

    # 建堆完成

# print(lst)  # 检验建堆是否完成

# 检验建堆是否成功

# lst = [i for i in range(10)]

# import random

# random.shuffle(lst)

# print(lst)

# heap_sort(lst)

# 结果

# [2, 3, 9, 7, 1, 8, 6, 0, 5, 4]

# [9, 7, 8, 5, 4, 2, 6, 0, 3, 1]

    # 接下来“农村包围城市”，从最后一个节点开始

    for i in range(n-1,-1,-1):  # i指向最后一个节点

        lst[0],lst[i] = lst[i],lst[0] # 堆顶元素lst[0]和最后一个节点位置互换

        shift(lst,0,i - 1) # i - 1代表新的high

    # return lst

lst1 = [i for i in range(10)]

import random

random.shuffle(lst1)

print(f"初始列表{lst1}")

 

heap_sort(lst1)

print(lst1)

# 结果

# 初始列表[2, 1, 8, 4, 6, 3, 7, 5, 9, 0]

# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

python中堆排序的内置模块

# 堆排序模块

import heapq  # q-->queue 优先队列（小的或大的先出）

import random

 

lst2 = [i for i in range(10)]

random.shuffle(lst2)

 

print(f"初始列表：{lst2}")

 

heapq.heapify(lst2) # 建堆，建的是小根堆

 

for i in range(len(lst2)):

    print(heapq.heappop(lst2),end=",")  # heappop每次弹出一个最小的元素

堆排序时间复杂度

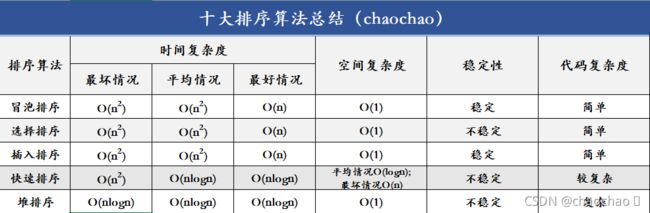
我们通过堆排序的原理发现，向下调整都是折半过程，紧接着还有一次“农村包围城市”，依次比较n次，所以堆排序的时间复杂度为O(nlogn)。

快速排序和堆排序相比，快速排序的效率还是高于堆排序。

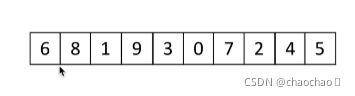
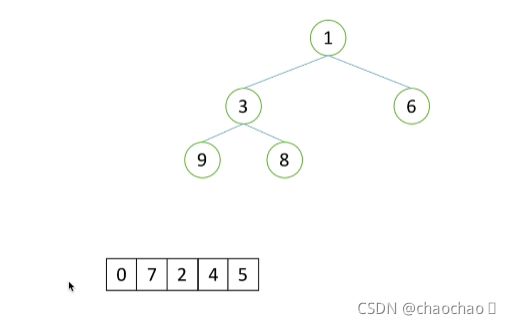
堆排序解决topk问题

现在有n个数，需要设计算法得到前k大的数。（k

解决思路：

1.排序后切片 ：O(nlogn)

即排序是nlogn，取k，时间复杂度为k，因此实际nlogn+k，此种情况对于n值很大的数据是效率很低 。

2.排序基础三人组 O(kn)

即例如冒泡排序n趟+k趟取topk。

3.堆排序思路：O(nlogk)

判断一个数是否进堆的过程是logK趟，然后有n个数因此是nlogk

堆排序解决思路：

1.取列表前k个元素建立一个小根堆，此时堆顶就是目前第k大的数

 2.依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整；（即接下来看0、7、2.....，比1小的就舍弃，比堆顶大的就放入堆顶并且向下调整）

3.遍历列表所有元素后，倒序弹出堆顶。

代码如下

import random

 

def shift(lst,low,high):  # low:对根节点的位置；high：堆最后一个元素的位置

    i = low  # 标记low

    j = 2 * i + 1  # j代表左孩子位置

    tmp = lst[low]  # 把堆顶存起来

    while j <= high:  # 只要j位置有元素，就循环

        if j + 1 <= high and lst[j+1] < lst[j]:  # 首先判断是否j这一层有右孩子(j + 1直的j这一层的另一个数)，其次判断j这一层元素的大小,j+1(有孩子)大于j，则j指向j+1

            j = j + 1 # j指向有孩子

        if lst[j] < tmp:  # 然后判断j和堆顶的元素（tmp）的大小，如果j位置的元素大于堆顶元素，则堆顶元素和j（左孩子）位置互换

            lst[i] = lst[j]

            i = j  # 继续看下一层

            j = 2 * i + 1

        else:  # tmp最大，则把tmp放到i的位置上

            lst[i] = tmp  # 把tmp放到某一级

            break

        lst[i] = tmp  # 把tmp放到叶子节点上

# topk

def topk(lst,k):

    heap = lst[0:k]

    for i in range((k-2)//2,-1,-1):

        shift(heap,i,k-1)

    # 1.建堆完成

    for i in range(k,len(lst)-1):

        if lst[i] > heap[0]:

            heap[0] = lst[i]

            shift(heap,0,k-1)

    # 2.遍历

    for i in range(k-1,-1,-1):

        heap[0],heap[i] = heap[i],heap[0]

        shift(heap,0,i-1)

    # 3.出数

    return heap

 

lst1 = [i for i in range(10)]

random.shuffle(lst1)

print(f"初始列表{lst1}")

result = topk(lst1,5)

print(result)

# 结果

# 初始列表[1, 8, 7, 2, 6, 3, 0, 9, 5, 4]

# [9, 8, 7, 6, 5]

十大排序之五大排序总结

稳定性说明：

3 2 1 2 4

稳定的排序可以保证左右两边的2的位置不变；

当我们换成字典来看时：

{"name":'a',"age":18}

{"name":'b',"age":19}

{"name":'a',"age":20}

如果按字母排序，稳定的排序，两个‘a’的位置不会改变

总的来说，挨个移动比较的排序算法为稳定的排序。

代码的复杂度：代表代码难不难写，应个人能力和主观感受而定。

创作不易，客官点个赞，评论一下吧！超超和你一起加油❤