模拟退火入门(求最值,解规划问题)
目录
-
- 求混合三角函数最值
- 求多元函数最值
- 书店买书问题
- 模拟退火需要注意的点
参考学习资料:
数学建模清风第二次直播:模拟退火算法
求混合三角函数最值
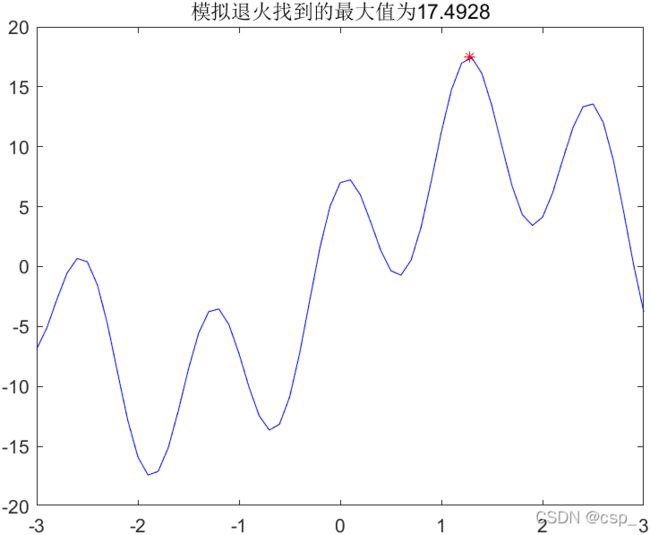
求解函数 y = 11 ∗ s i n ( x ) + 7 ∗ c o s ( 5 ∗ x ) y = 11*sin(x) + 7*cos(5*x) y=11∗sin(x)+7∗cos(5∗x)在 [ − 3 , 3 ] [-3,3] [−3,3]内的最大值
思路:
- 给出函数表达式
- 绘制函数的图形
- 参数初始化
- 随机生成一个初始解
- 定义一些保存中间过程的量,方便输出结果和画图
- 模拟退火过程
- 画出每次迭代后找到的最大y的图形
技巧:
randn:产生均值为0,方差 σ 2 σ^2 σ2 = 1,标准差 σ σ σ = 1的正态分布的随机数或矩阵的函数
scatter是绘制二维散点图的函数,设置其返回值为 h h h 可以得到图形的句柄,方便未来我们对其位置进行更新
代码:
Obj_fun1.m
function y = Obj_fun1(x)
y = 11*sin(x) + 7*cos(5*x);
end
main.m
tic
clear; clc
x = -3:0.1:3;
y = 11*sin(x) + 7*cos(5*x);
figure
plot(x,y,'b-')
hold on
narvs = 1; % 变量个数
T0 = 100; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 200; % 最大迭代次数
Lk = 100; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
x_lb = -3; % x的下界
x_ub = 3; % x的上界
x0 = zeros(1,narvs);
for i = 1: narvs
x0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun1(x0);
h = scatter(x0,y0,'*r');
max_y = y0; % 初始化最优解
MAXY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的max
for iter = 1 : maxgen
for i = 1 : Lk
y = randn(1,narvs);
z = y / sqrt(sum(y.^2)); % !!根据新解的产生规则计算z
x_new = x0 + z*T; % 根据新解的产生规则计算x_new的值
% !!如果这个新解的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x_new(j) < x_lb(j)
r = rand(1);
x_new(j) = r*x_lb(j)+(1-r)*x0(j);
elseif x_new(j) > x_ub(j)
r = rand(1);
x_new(j) = r*x_ub(j)+(1-r)*x0(j);
end
end
x1 = x_new;
y1 = Obj_fun1(x1);
if y1 > y0
x0 = x1; % 更新当前解为新解
y0 = y1;
else
p = exp(-(y0 - y1)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p
x0 = x1;
y0 = y1;
end
end
% 判断是否要更新找到的最佳的解
if y0 > max_y
max_y = y0;
best_x = x0;
end
end
MAXY(iter) = max_y; % 保存本轮外循环结束后找到的最大的y
T = alfa*T; % 温度下降
pause(0.1) % 暂停一段时间(单位:秒)后再接着画图
h.XData = x0; % 更新散点图句柄的x轴的数据(此时解的位置在图上发生了变化)
h.YData = Obj_fun1(x0); % 更新散点图句柄的y轴的数据(此时解的位置在图上发生了变化)
end
disp('最佳的位置是:'); disp(best_x)
disp('此时最优值是:'); disp(max_y)
pause(0.05)
h.XData = []; h.YData = []; % 将原来的散点删除
scatter(best_x,max_y,'*r'); % 在最大值处重新标上散点
title(['模拟退火找到的最大值为', num2str(max_y)]) % 加上图的标题
figure
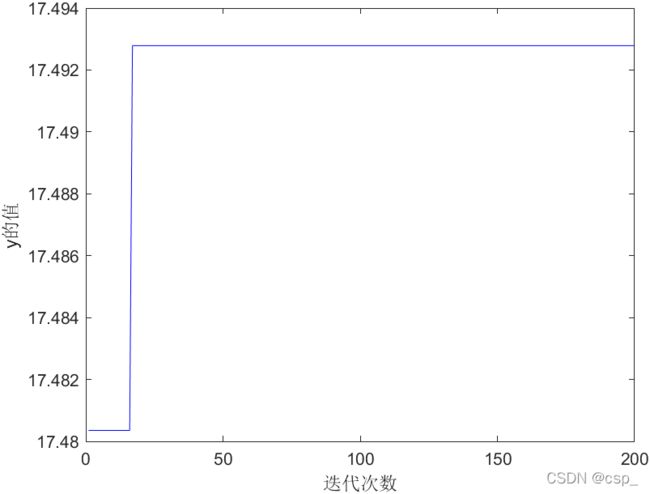
plot(1:maxgen,MAXY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc
最佳的位置是:
1.2747
此时最优值是:
17.4928
历时 6.819488 秒。
求多元函数最值
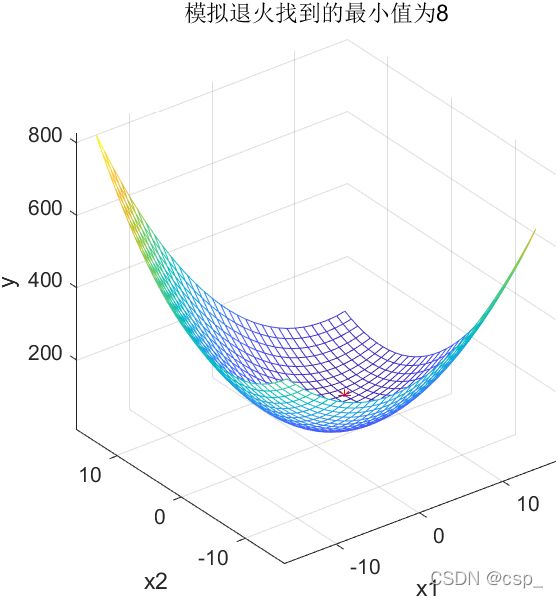
求解函数 y = x 1 2 + x 2 2 − x 1 ∗ x 2 − 10 ∗ x 1 − 4 ∗ x 2 + 60 y = x_{1}^2+x_{2}^2-x_{1}*x_{2}-10*x_{1}-4*x_{2}+60 y=x12+x22−x1∗x2−10∗x1−4∗x2+60在 [ − 15 , 15 ] [-15,15] [−15,15]内的最小值
技巧:
meshgrid可以生成二维网格,用法为:[x y]=meshgrid(a b); 其中 a 和 b 是一维数组,如a=[1 2]; b= [2 3 4]; 则生成的 X 和 Y 都是为 2X3 维的矩阵
mesh可以画网格图片,将一个矩阵绘制成三维图像,实际上就是给出一对坐标(x,y),来画矩阵z(x,y)的值
代码:
tic
clear; clc
figure
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1'); ylabel('x2'); zlabel('y'); % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on % 不关闭图形,继续在上面画图
narvs = 2;
T0 = 100;
T = T0;
maxgen = 200;
Lk = 100;
alfa = 0.95;
x_lb = [-15 -15];
x_ub = [15 15];
x0 = zeros(1,narvs);
for i = 1: narvs
x0(i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(1);
end
y0 = Obj_fun2(x0);
h = scatter3(x0(1),x0(2),y0,'*r');
min_y = y0;
MINY = zeros(maxgen,1);
for iter = 1 : maxgen
for i = 1 : Lk
y = randn(1,narvs);
z = y / sqrt(sum(y.^2)); % 根据新解的产生规则计算z
x_new = x0 + z*T; % 根据新解的产生规则计算x_new的值
% 如果这个新解的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x_new(j) < x_lb(j)
r = rand(1);
x_new(j) = r*x_lb(j)+(1-r)*x0(j);
elseif x_new(j) > x_ub(j)
r = rand(1);
x_new(j) = r*x_ub(j)+(1-r)*x0(j);
end
end
x1 = x_new;
y1 = Obj_fun2(x1);
if y1 < y0
x0 = x1;
y0 = y1;
else
p = exp(-(y1 - y0)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p
x0 = x1;
y0 = y1;
end
end
% 判断是否要更新找到的最佳的解
if y0 < min_y % 如果当前解更好,则对其进行更新
min_y = y0; % 更新最小的y
best_x = x0; % 更新找到的最好的x
end
end
MINY(iter) = min_y; % 保存本轮外循环结束后找到的最小的y
T = alfa*T;
pause(0.02)
h.XData = x0(1); % 更新散点图句柄的x轴的数据(此时解的位置在图上发生了变化)
h.YData = x0(2); % 更新散点图句柄的y轴的数据(此时解的位置在图上发生了变化)
h.ZData = Obj_fun2(x0); % 更新散点图句柄的z轴的数据(此时粒子的位置在图上发生了变化)
end
disp('最佳的位置是:'); disp(best_x)
disp('此时最优值是:'); disp(min_y)
pause(0.5)
h.XData = []; h.YData = []; h.ZData = []; % 将原来的散点删除
scatter3(best_x(1), best_x(2), min_y,'*r'); % 在最小值处重新标上散点
title(['模拟退火找到的最小值为', num2str(min_y)]) % 加上图的标题
%% 画出每次迭代后找到的最小y的图形
figure
plot(1:maxgen,MINY,'b-');
xlabel('迭代次数');
ylabel('y的值');
toc
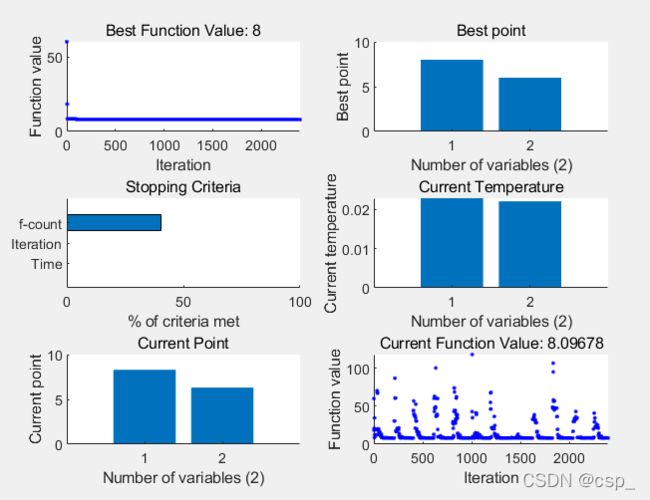
最佳的位置是:
8.0005 6.0000
此时最优值是:
8.0000
历时 7.040709 秒。
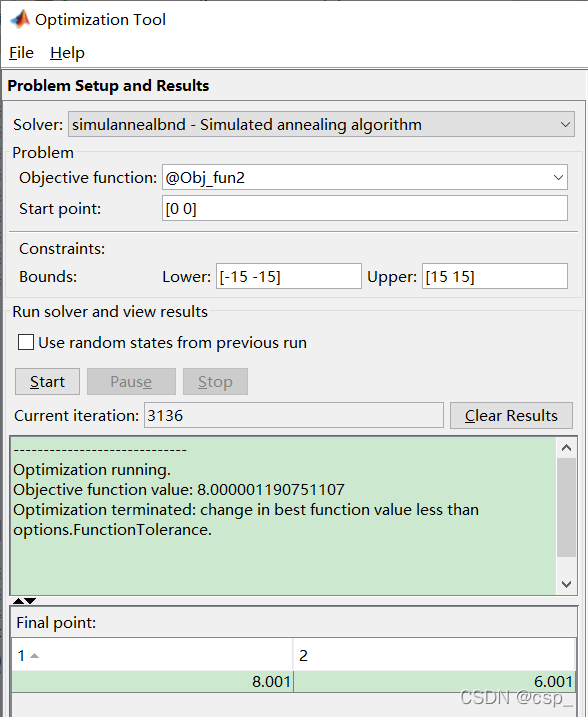
生成可以调用的函数代码(Generate code):
function [x,fval,exitflag,output] = res(x0,lb,ub)
%% This is an auto generated MATLAB file from Optimization Tool.
%% Start with the default options
options = optimoptions('simulannealbnd');
%% Modify options setting
options = optimoptions(options,'Display', 'off');
options = optimoptions(options,'HybridInterval', 'end');
[x,fval,exitflag,output] = ...
simulannealbnd(@Obj_fun2,x0,lb,ub,options);
输入[x,fval,exitflag,output]=res([0 0],[-15 -15],[15 15])运行即可
书店买书问题
某同学要从15 家书店购买 20 本书(每种书买一本即可),已知每本书籍在不同商家的售价以及每个商家的单次运费,请给该同学制定最省钱的选购方案(在同一个店买多本书也只会收取一次运费)
M矩阵:( M [ i ] [ j ] M[i][j] M[i][j]为第 j j j本书在第 i i i家店的价格)
31 31 41 21 25 28 23 34 38 29 38 33 32 24 23 20 23 26 21 32
40 27 38 26 23 29 24 22 37 29 32 34 31 27 31 22 26 27 25 27
35 25 41 20 26 21 37 24 34 22 42 31 37 26 28 23 23 21 26 28
33 26 22 29 38 25 34 32 34 24 27 25 26 31 39 34 21 21 41 34
33 29 36 24 21 24 33 28 25 29 24 26 26 29 37 24 25 25 32 27
25 32 20 21 20 32 42 22 33 24 35 28 38 26 34 21 39 25 40 23
35 22 35 29 29 26 38 30 27 21 25 30 33 32 30 32 25 23 26 23
36 22 39 26 34 25 32 23 35 29 20 32 34 31 25 24 38 25 29 25
32 23 22 21 27 22 20 30 27 24 41 27 33 27 29 22 31 26 25 24
27 28 36 22 38 27 29 33 29 25 29 33 34 25 24 22 37 27 42 30
39 28 26 27 37 28 23 31 35 27 30 28 20 32 31 21 32 31 43 21
22 28 38 33 40 23 43 30 35 24 23 26 36 23 34 24 40 24 41 30
30 25 27 32 27 30 40 27 36 22 30 29 21 32 41 33 33 29 31 31
34 21 27 29 25 21 36 33 21 28 21 30 35 22 22 24 40 27 25 23
31 27 24 25 39 23 40 30 22 28 38 31 21 29 21 25 40 22 31 35
freight矩阵:( f r e i g h t [ i ] freight[i] freight[i]表示第 i i i家店的运费)
10
10
14
7
12
5
10
8
14
9
12
6
11
5
9
calculate_money.m
function money = calculate_money(way,freight,M,b)
index = unique(way);
money = sum(freight(index));
% 总花费:刚刚计算出来的运费 + 五本书的售价
for i = 1:b
money = money + M(way(i),i);
end
end
gen_new_way.m
function way1 = gen_new_way(way0, s, b)
% way0:原来的买书方案,是一个1*b的向量,每一个元素都位于1-s之间
index = randi([1, b],1) ;
way1 = way0;
way1(index) = randi([1, s],1);
end
main.m
tic
rng('shuffle') % 控制随机数的生成,否则每次打开matlab得到的结果都一样
[s, b] = size(M); % s是书店的数量,b是要购买的书的数量
T0 = 1000; % 初始温度
T = T0; % 迭代中温度会发生改变,第一次迭代时温度就是T0
maxgen = 500; % 最大迭代次数
Lk = 200; % 每个温度下的迭代次数
alfa = 0.95; % 温度衰减系数
way0 = randi([1, s],1,b); % 在1-s这些整数中随机抽取一个1*b的向量,表示这b本书分别在哪家书店购买
money0 = calculate_money(way0,freight,M,b); % 调用calculate_money函数
min_money = money0; % 初始化找到的最佳的解对应的花费为money0
MONEY = zeros(maxgen,1); % 记录每一次外层循环结束后找到的min_money (方便画图)
for iter = 1 : maxgen
for i = 1 : Lk
way1 = gen_new_way(way0,s,b); % 调用gen_new_way函数生成新解
money1 = calculate_money(way1,freight,M,b);
if money1 < money0
way0 = way1;
money0 = money1;
else
p = exp(-(money1 - money0)/T); % 根据Metropolis准则计算一个概率
if rand(1) < p
way0 = way1;
money0 = money1;
end
end
% 判断是否要更新找到的最佳的解
if money0 < min_money
min_money = money0;
best_way = way0;
end
end
MONEY(iter) = min_money; % 保存本轮外循环结束后找到的最小花费
T = alfa*T;
end
disp('最佳的方案是:'); disp(mat2str(best_way))
disp('此时最优值是:'); disp(min_money)
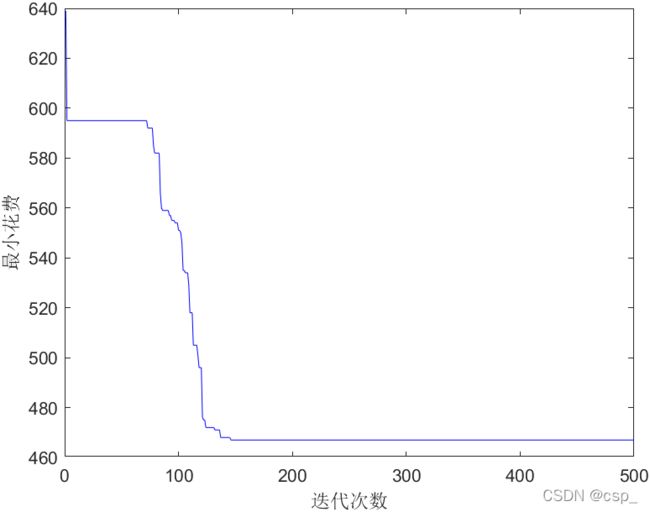
%% 画出每次迭代后找到的最佳方案的图形
figure
plot(1:maxgen,MONEY,'b-');
xlabel('迭代次数');
ylabel('最小花费');
toc
最佳的方案是:
[6 14 6 6 6 14 1 6 14 6 14 4 4 14 14 1 4 4 1 6]
此时最优值是:
467
历时 1.546311 秒。
模拟退火需要注意的点
- 对参数的选择(例如初始的温度)以及退火流程的设置需要经验,参数设置的不恰当得到的解可能会很差。因此我们可以多次尝试不同的参数,观察求解时间和求解结果,以此来对参数进行修改
- 新解的构造至关重要,新解不能距离旧解“太远”,否则旧解的信息不能被新解反映;同时新解也不能距离旧解“太近”,否则容易陷入局部最优
- 如果优化问题中的约束非常多,那么这时候构造新解就有很大的技巧性。如果构造的新解不在约束条件内,虽然我们可以重新构造新解,但这样会增加我们的计算量