快速入门时间复杂度&空间复杂度
目录
一、时间复杂度
1)O(n)的含义
2)复杂表达式的简化
3)O(n)不一定优于O(n^2)
4)递归的时间复杂度
二、空间复杂度
1) O(1)空间复杂度
2)O(n)空间复杂度
3)O(mn)空间复杂度
4)递归算法空间算法复杂度分析
一、时间复杂度
1)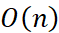 的含义
的含义
- 程序消耗的时间用算法的操作单元数来表示
- 假设数据的规模为n,则用f(n)表示操作单元数的大小,而f(n)常被简化
- O表示的是一般的情况,而不是上界或下界。并且它是在数据量级非常大的情况下所展现出的时间复杂度
- 因为O代表的是一个一般的情况,所以当用例不同时,算法的时间复杂度不同,需要具体分析
2)复杂表达式的简化
表达式简化遵循以下两个原则:
- 去掉常数项
- 只保留最高项
不难想象,当n趋一个非常大的数量级的时候,最高项将其决定性作用。但是若常数项也是一个非常大的数量级,那我们就不可以轻易将其舍去。
3) 不一定优于
不一定优于
由上面简化法则我们可以看到,常数项是被忽略的,如![]() 与
与 ![]() ,当n < 20时前者的操作单位数是小于后者的。
,当n < 20时前者的操作单位数是小于后者的。
所以在决定使用什么算法的时候并不是算法的时间复杂度越低越好,还需要考虑数据的规模
那为什么我们默认![]() 时间复杂度低于
时间复杂度低于![]() 呢?正如前面提到的关于O的定义:它是在数据量级非常大的情况下所展现出的时间复杂度,所以我们默认前者的时间复杂度更优。
呢?正如前面提到的关于O的定义:它是在数据量级非常大的情况下所展现出的时间复杂度,所以我们默认前者的时间复杂度更优。
4)递归的时间复杂度
⭐递归的时间复杂度 = 递归次数 X 每次递归的操作次数。
现在我们从一道面试题来分析时间复杂度:求x的n次方
①直观的for循环遍历
int fuc1(int n)
{
int ret = 1;
for (int i = 1; i < n; i++)
ret *= i;
return ret;
}②递归版本1
int fuc2(int n,int x)
{
if (n == 0)
return 1;
if (n == 1)
return x;
return x * fuc2(n - 1, x);
}【分析】递归次数为n次,每次相乘的时间复杂度为![]() ,所以时间复杂度仍为
,所以时间复杂度仍为![]()
③递归版本2
int fuc3(int n, int x)
{
if (n == 0)
return 1;
if (n == 1)
return x;
if (n % 2 == 1)
return fuc3(n / 2, x) * fuc3(n / 2, x) * x;//奇数次幂的情况
return fuc3(n / 2, x) * fuc3(n / 2, x); //偶数次幂的情况
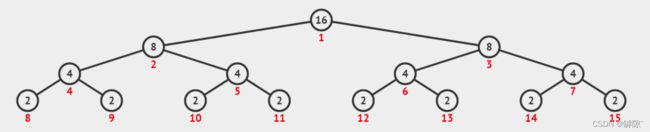
}【分析】上面代码的时间复杂度为![]() 吗?我们可以画二叉树来理解,以n = 16为例
吗?我们可以画二叉树来理解,以n = 16为例
每一个结点都表示需要进行一次递归,因此结点数代表着递归次数,所以先我们计算二叉树结点数
将深度公式代入结点总和公式我们可以得出, 节点数 = n - a(a为某个常数),所以时间复杂度还是![]()
④递归版本3
int fuc4(int n, int x)
{
if (n == 0)
return 1;
else if (n == 1)
return 1;
int t = fuc4(n / 2, x);
if (n % 2 == 1)
return t * t * x;
return t * t;
}通过将递归操作抽离出来从而减少递归次数,我们真正实现了时间复杂度为![]()
我们再分析一下求斐波那契数列函递归解法时间复杂度:
int fib(int n)
{
if (n <= 0)
return 1;
if (n == 1)
return 1;
return fib(n - 1) + fib(n - 2);
}同样的我们可以画二叉树来分析。求第k个斐波那契数,我们不难想象,我们将构造出一个深度为k的二叉树,深度为k的二叉树最多有 ![]() 个结点,所以我们得出该算法的时间复杂度为
个结点,所以我们得出该算法的时间复杂度为![]() 。优化的思路和上述求x的n次方的思路一样,主要是减少递归的调用次数
。优化的思路和上述求x的n次方的思路一样,主要是减少递归的调用次数
int fib(int first, int second, int n)
{
if (n <= 0)
return 0;
if (n < 3)
return 1;
else if (n == 3)
return first + second;
else
return fib(second, first + second, n - 1);
}二、空间复杂度
1)  空间复杂度
空间复杂度
程序占用空间不随n的变化而变化,即占用的空间是一个常数
for(int j = 0; j < n; j++)
{
j++;
}程序占用的空间与n无关,上图中之涉及为j分配内存空间,是一个固定的常量
2)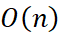 空间复杂度
空间复杂度
程序占用空间随n增长而线性增长;
int arr[n];3)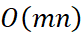 空间复杂度
空间复杂度
常常是定义一个二维集合,集合的大小与集合的长与宽相管
int arr[row * col];4)递归算法空间算法复杂度分析
⭐递归算法空间复杂度 = 每次递归的空间复杂度 X 递归深度(递归调用栈的最大长度)
我们同样来分析上面提到的求斐波那契数函数的空间复杂度:
int f(int n)
{
if (n <= 0)
return 1;
if (n == 1)
return 1;
return f(n - 1) + f(n - 2);
} 在递归的过程中依次将f(5),f(4), f(3),f(2),f(1)压栈,每一次调用所占用的空间都为所以占用的空间为![]() ,所以上述代码的空间复杂度为
,所以上述代码的空间复杂度为![]()
我们再来分析递归实现的二分查找的空间复杂度:
int binary_search(int arr[], int l, int r, int x)
{
if (r >= l)
{
int mid = l + (r - l) / 2; //避免先加后除产生溢出的错误
if (arr[mid] == x)
return mid;
else if (arr[mid] < x)
return binary_search(arr, mid + 1, r ,x);
else
return binary_search(arr, l, mid - 1, x);
}
return -1;
}每次递归所占用的空间都是一定的,所以每次递归的空间复杂度为![]() ,而递归的最大深度为
,而递归的最大深度为
本文内容参考学习参考于《代码随想录》