算法工程师6——数据结构与算法主要知识概览
数据结构一开始觉得很难,实际上基础的还是特别简单的,首先把本文的知识搞懂了,没有任何难点,两个小时全部复习一遍,本文只涉及到一些结构,算法部分涉及的较少。
重点
重点
重点
无论是数据结构还是算法,主要的是思路,思路出来了,编程就好编了,结果就出来了。
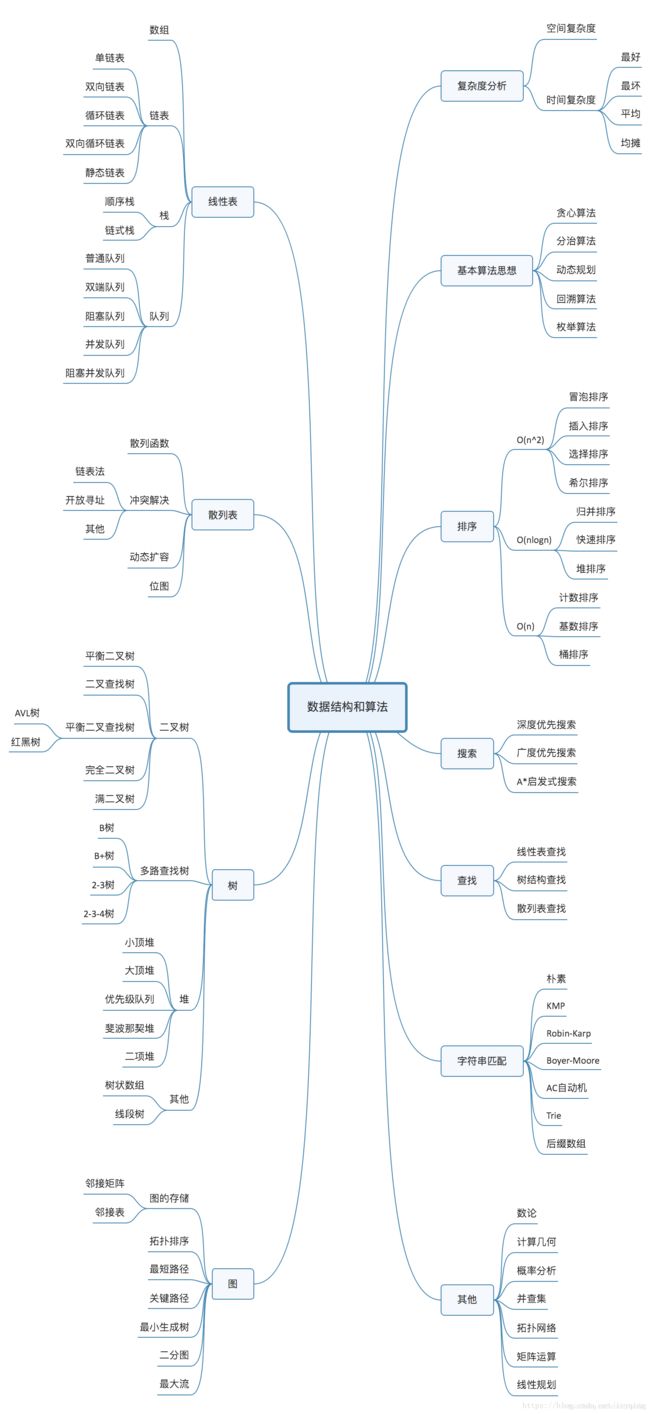
数据结构与算法
- 1 基本概念
-
- 1.1 基本概念
- 1.2 内存存储结构
- 1.3 数据结构分类
- 1.4 线性结构的存储方式
- 2 几种线性结构
-
- 2.1顺序表
-
- 2.1.1 顺序表两种存储方式
- 2.1.2 顺序表增加删除
- 2.2 链表
- 2.3 栈(先进后出)
- 2.4 队列(先进先出)
- 2.4 双端队列
- 3 排序
-
- 3.1 冒泡排序(必背)
- 3.2 选择排序(必背)
- 3.3 插入排序(必背)
- 3.4 快速排序(必背)
- 4 查找算法
-
- 4.1 二分查找
- 5 树
- 5.1 树
- 5.2 二叉树
- 5.3 完全二叉树代码实现
- 5.4 广度优先遍历和深度优先遍历
- 5.5 遍历结果反推二叉树结构
- 6代码实现
-
- 6.1 单向链表的代码实现
- 6.2 栈的实现
- 6.3 队列的实现
- 6.4 双端队列的实现
- 6.5 冒泡排序
- 6.6 选择排序
- 6.7 插入排序(10分钟)
- 6.8 快速排序
- 6.9 二分查找
- 6.10 广义二叉树的实现和4种遍历
1 基本概念
1.1 基本概念
数据结构就是存储组织数据的方式
算法实现业务的各种方法和思路就是,代码只是实现算法的方式。
时间效率=操作步骤数量*操作步骤执行时间
数据结构指的是“一组数据的存储结构”,算法指的是“操作数据的一组方法”。
数据结构是为算法服务的,算法是要作用再特定的数据结构上的。
最常用的数据结构预算法:
数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Tire树
算法: 递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
算法复杂度是算法的时间复杂度和空间复杂度的合称
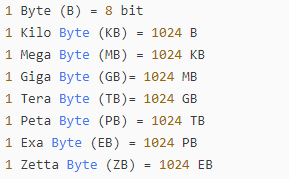
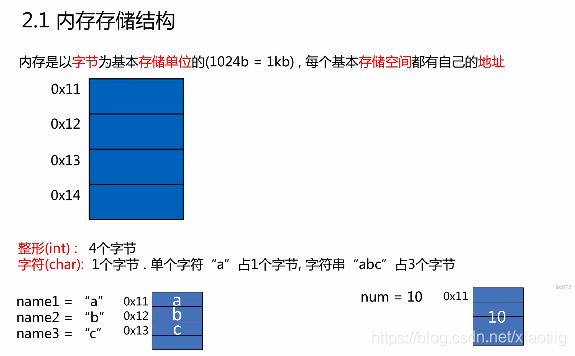
1.2 内存存储结构
也就是以1个字节为单位,8个bit比特位为单位
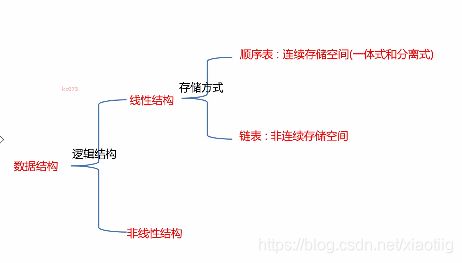
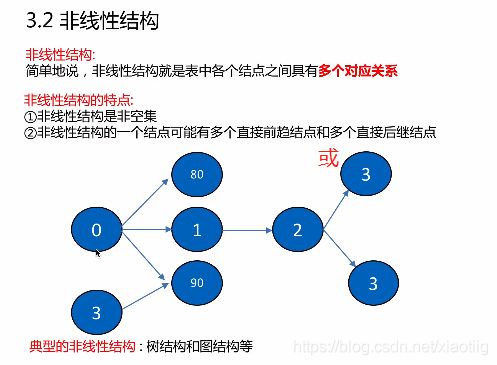
1.3 数据结构分类
1.4 线性结构的存储方式
2 几种线性结构
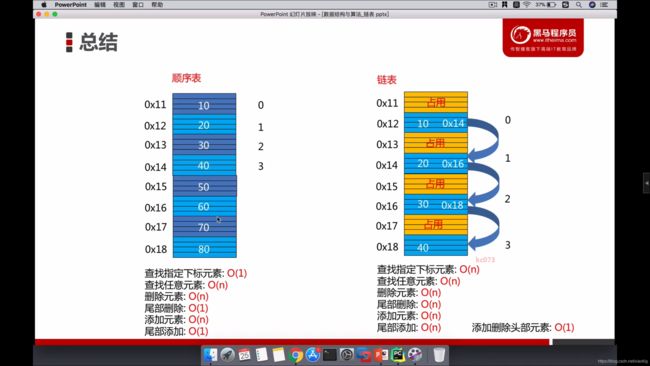
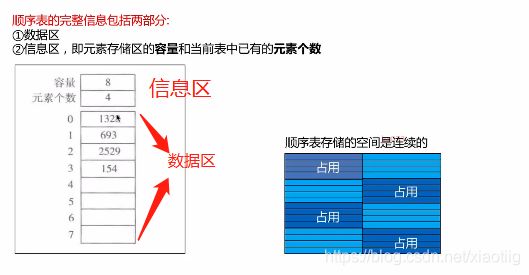
2.1顺序表
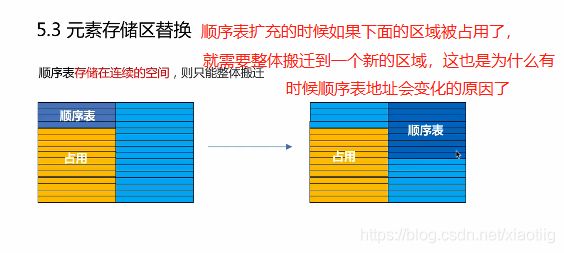
2.1.1 顺序表两种存储方式
2.1.2 顺序表增加删除
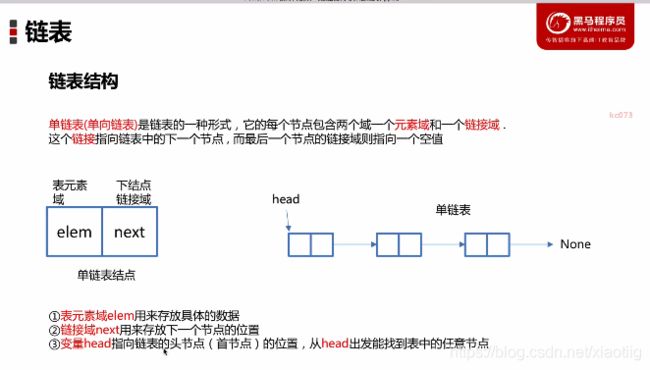
2.2 链表
链表是有一个一个节点组成的,就和python中的列表几乎是一样的。

2.3 栈(先进后出)
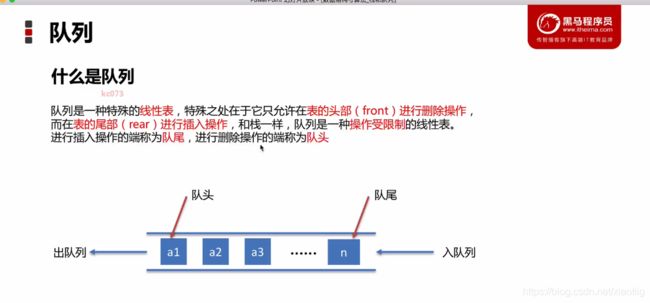
2.4 队列(先进先出)
2.4 双端队列
3 排序
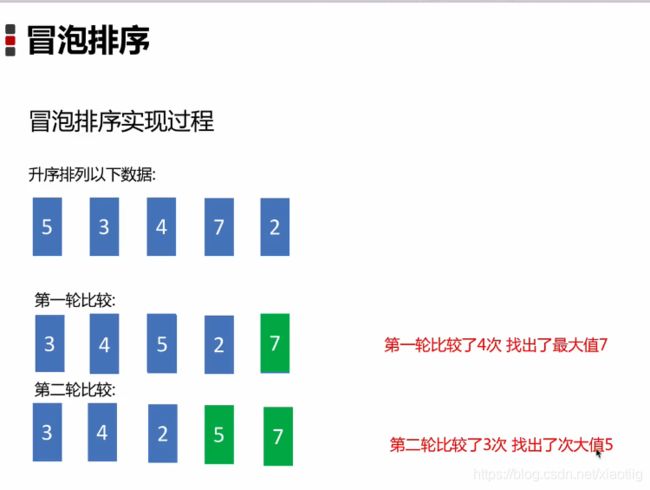
3.1 冒泡排序(必背)
3分钟绝对可以理解
我是看的黑马程序员的人工智能课程视频
第一轮:每次都从头才是比较两个元素,如果第2个比第1个小,就调换位置。再比较第2个元素和第3个元素,一直到最后。这样最大的元素就跑到了最后了
第二轮:同样道理,这样第二大的元素就跑到了倒数第二的位置
…
有N个元素,就一直进行N-1轮,每一轮都比上次的比较次数少一次。
3.2 选择排序(必背)
3.3 插入排序(必背)
3分钟就能搞懂,道理简单,
但是代码需要多花时间理解一下,10分钟思考一下代码
插入排序就是把数据分成两组,
先取第一个数,然后将第一个数和剩下的数分为两部分,前部分的数是排序好的数,后一部分是待排序的数,每次取后一部分的数插入到前一部分排序好的数中,从而实现排序。


3.4 快速排序(必背)
排序里面最复杂的算法,3分钟搞懂思想,很简单
代码复杂,30分钟理解
![]()
4 查找算法
4.1 二分查找
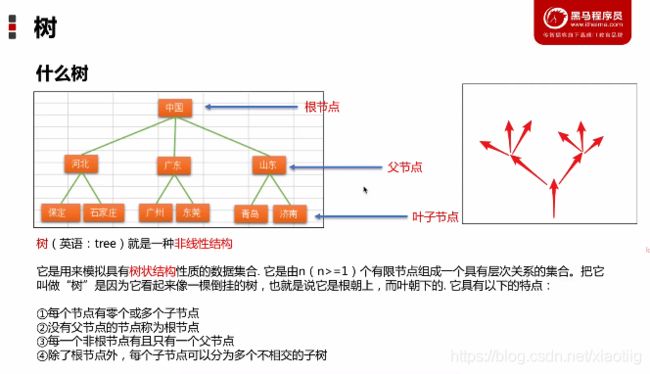
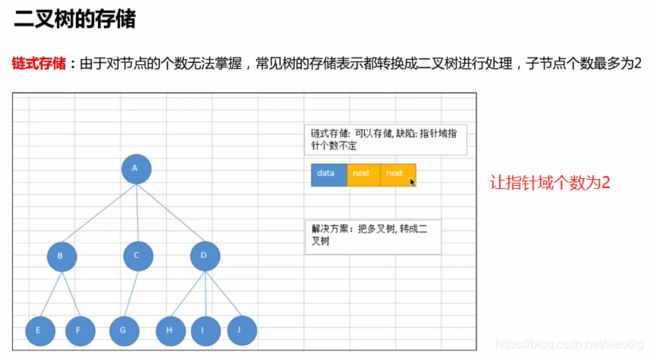
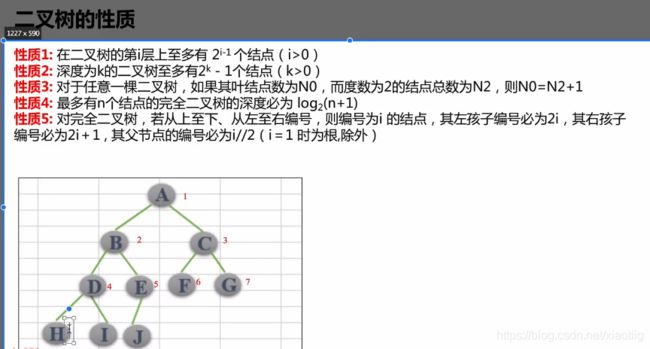
5 树
5.1 树
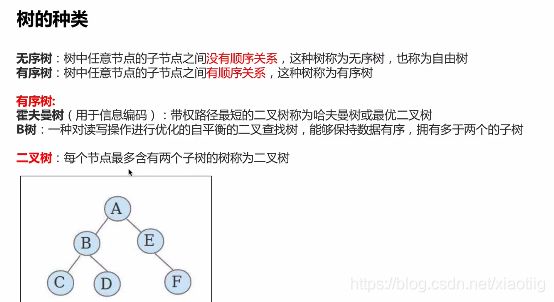
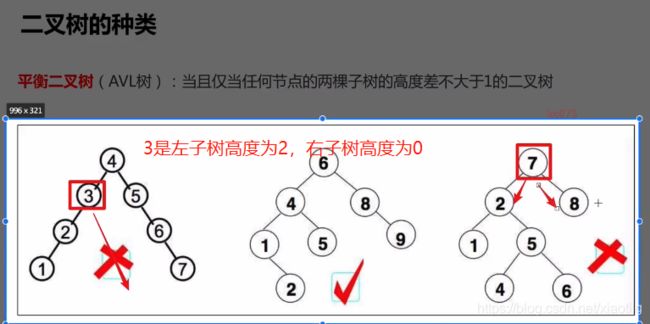
5.2 二叉树
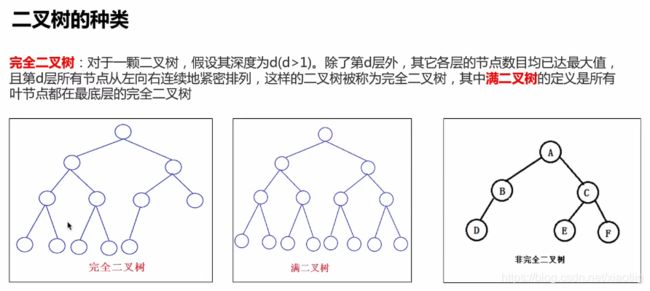
5.3 完全二叉树代码实现
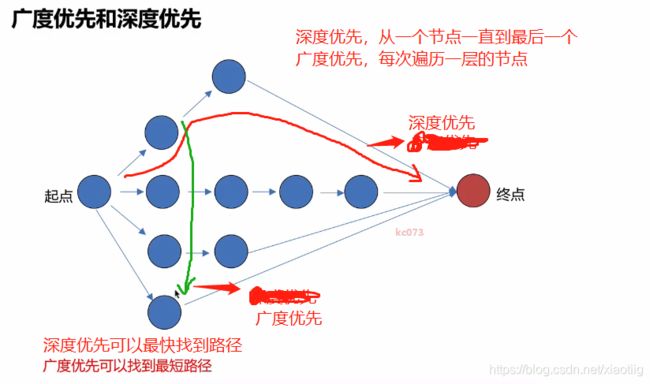
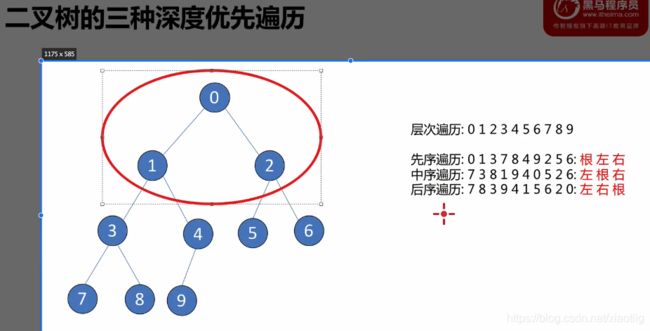
5.4 广度优先遍历和深度优先遍历
5.5 遍历结果反推二叉树结构
6代码实现
6.1 单向链表的代码实现
# 链表的实现
# 理解链表关键理解了每个节点除了有自己的元素,还有另外的一个指向就可以了
# 晓码实现
# 参考黑马程序员人工智能课程第二阶段的数据结构课程实现
class SingleNode(object):
"""链表节点的实现"""
# 每个节点存储两个元素,一个是自己的内容,一个是下一个节点的引用
def __init__(self,item):
# item:存放元素
self.item = item
# next: 标识下一个节点
self.next = None
# 单链表的实现
# 链表的空判断,长度,遍历
# 链表的增删改查
# head: 头节点,和cur游标一样,head和cur都是头节点
class SingleLinkList(object):
"""实现单链表"""
# 有节点就增加节点,没有就是默认为空
def __init__(self,node=None):
# head: 首节点
self.head = node
def is_empty(self):
"""判断链表是否为空"""
if self.head is None:
return True
else:
return False
def length(self):
"""获取链表的长度"""
# cur 就是一个一个节点
cur = self.head
# 计数
count = 0
# 如果这个节点不为空,就指向下一个节点
while cur is not None:
cur = cur.next
count +=1
return count
def travel(self):
"""链表的遍历"""
cur = self.head
while cur is not None:
print(cur.item)
cur = cur.next
# add方法里用到item,因为下面的SingleLinkList用到了这个参数
def add(self,item):
"""链表头部增加节点"""
# 必须是新节点先指向头节点,再让头节点指向新节点,反过来不行
node = SingleNode(item)
node.next = self.head
self.head = node
def append(self,item):
"""尾部增加节点"""
node = SingleNode(item)
if self.is_empty():
self.head = node
else:
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = node
def insert(self,pos,item):
"""指定位置插入元素"""
if pos<=0:
self.add(item)
elif pos>=self.length():
self.append(item)
else:
node = SingleNode(item)
cur = self.head
count = 0
# 1 找到插入的位置
while count < pos-1:
cur = cur.next
count +=1
# 2完成插入新节点
node.next = cur.next
cur.next = node
def remove(self,item):
"""删除节点"""
cur = self.head
pre = None
while cur is not None:
# 找到了要删除的元素
if cur.item == item:
# 要删除的元素在头部
if cur == self.head:
self.head = cur.next
# 不在头部找到了删除元素
else:
pre.next = cur.next
# 这里必须有ruturn,否则程序结束不了,因为一直会执行上面的判断和else语句
return
# 没有找到要删除的元素
else:
pre = cur
cur = cur.next
def search(self,item):
"""查找元素是否存在"""
cur = self.head
while cur is not None:
# 如果找到了指定元素
if cur.item == item:
print("存在")
return True
cur = cur.next
print("不存在")
return False
if __name__ == "__main__":
node1 = SingleNode(10)
print("节点元素", node1.item)
print("节点标识的下一个节点", node1.next)
Link1 = SingleLinkList()
print("单链表1的头位置",Link1.head)
Link2 = SingleLinkList(node1)
print("单链表2的头位置",Link2.head)
print("单链表2的头元素",Link2.head.item)
print("Link1判空:",Link1.is_empty())
print("Link2判空:", Link1.is_empty())
print("头部增加元素:")
Link2.add(9)
Link2.travel()
print("尾部增加元素:")
Link2.append(11)
Link2.travel()
# 指定位置2增加节点,元素为0
print("插入元素:")
Link2.insert(2,0)
Link2.travel()
print("删除元素:")
Link2.remove(11)
Link2.travel()
print("查找元素是否存在:")
Link2.search(9)
Link2.search(98)
6.2 栈的实现
# 尾部插入删除数据
# append(item),pop()
class Stack(object):
"""栈,先进后出"""
def __init__(self):
# __items是一个列表
self.__items = []
def push(self,item):
"""出栈"""
self.__items.append(item)
def pop(self):
# 列表的pop方法就是删除结尾元素
self.__items.pop()
def travel(self):
"""遍历"""
for i in self.__items:
print(i)
my_stack = Stack()
my_stack.push(1)
my_stack.push(2)
my_stack.push(3)
my_stack.travel()
# 出栈 3 先出去
my_stack.pop()
my_stack.travel()
6.3 队列的实现
# 队列
class Queue(object):
def __init__(self):
# 用一个列表存储数据
self.items = []
def enqueue(self,item):
"""队列尾部添加元素"""
self.items.append(item)
def dequeue(self):
"""队列头部开始删除元素,出队列"""
self.items.pop(0)
def is_empty(self):
"""判断是否为空"""
return self.items == []
def size(self):
"""返回队列长度"""
return len(self.items)
queue1 = Queue()
queue1.enqueue(1)
queue1.enqueue(2)
queue1.enqueue(3)
print("进队列")
print(queue1.items)
print("出队列")
queue1.dequeue()
print(queue1.items)
6.4 双端队列的实现
# 双端队列
class Deque(object):
"""双端队列"""
def __init__(self):
self.items = []
def is_empty(self):
return self.items == []
def size(self):
"""返回队列大小"""
return len(self.items)
def add_front(self,item):
"""头部添加数据"""
self.items.insert(0,item)
def add_rear(self,item):
"""尾部添加数据"""
self.items.append(item)
def remove_front(self):
"""头部删除数据"""
self.items.pop(0)
def remove_rear(self):
"""尾部删除数据"""
self.items.pop()
deque1 = Deque()
deque1.add_front(1)
deque1.add_front(2)
deque1.add_rear(3)
print(deque1.items)
deque1.remove_front()
print(deque1.items)
deque1.remove_rear()
print(deque1.items)
6.5 冒泡排序
# 实现冒泡排序
# 参考黑马程序员人工智能课程
def bubble_sort(alist):
"""冒泡排序"""
# 数列的长度
n = len(alist)
# 计数
count = 0
# 控制比较轮数
for j in range(0,n-1):
# 控制每一轮的比较次数
for i in range(0,n-j-1):
# 比较两个数字
if alist[i]>alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
count +=1
# 如果遍历了一遍发现没有数字进行交换,说明原来的数字就是有序的,退出循环
if count ==0:
break
if __name__ == "__main__":
alist = [5,3,4,7,2]
bubble_sort(alist)
print("排序后:",alist)
6.6 选择排序
# 选择排序
# 参考黑马人工智能课程
def select_sort(alist):
"""选择排序"""
# 列表的长度
n = len(alist)
for j in range(0,n-1):
# 先假定第一个值是最小的
min_index = j
for i in range(j+1,n):
# 进行比较获得最小值
if alist[i]<alist[min_index]:
min_index = i
# 如果假定的最小值下标发生了变化,就进行交换
if min_index != j:
alist[j], alist[min_index] = alist[min_index], alist[j]
if __name__ == "__main__":
alist = [5,3,4,7,2]
select_sort(alist)
print("排序后:",alist)
6.7 插入排序(10分钟)
理解的时候拿笔找个案例模拟一下过程一下就理解了
前半部分是排序好的,后半部分每次跟前半部分比,从小到大排序,每次选第j个元素插入到前面j-1个元素中合适的位置
# 插入排序
def insert_sort(alist):
"""插入排序"""
# 列表的长度
n = len(alist)
# 控制轮数
for j in range(1,n):
# range(j, 0, -1)就是【j,j-1,j-2,...1】
# 找到合适的位置放置数据
# 前半部分是排序好的,后半部分每次跟前半部分比,从小到大,每次选第j个元素插入到前面j-1个元素中合适的位置
for i in range(j, 0, -1):
if alist[i] <alist[i-1]:
alist[i], alist[i-1] = alist[i-1], alist[i]
else:
break
if __name__ == "__main__":
alist = [5,3,4,7,2]
insert_sort(alist)
print("排序后:",alist)
6.8 快速排序
# 快速排序
# 比较复杂,需要花30分钟时间好好想想
# 开始实现和理解不了代码,先简化,尝试着就只进行一轮该怎么实现,就是根据一个值放到左右两边怎么实现
def quick_sort(alist,start,end):
"""快速排序"""
# 递归的结束条件
if start >= end:
return
# 界限值,每次都需要找一个界限
mid = alist[start]
# 左右的游标
left = start
right = end
while left< right:
# 从右边开始找寻小于mid的值,归类到左边
while alist[right] >= mid and left < right:
right -= 1
# 这一步直接可以把alist[right]赋给alist[left],是因为alist[left]的值已经给了mid或者给了alist[right]
alist[left] = alist[right]
# 从左边开始找寻大于mid的值,归类到右边
while alist[left] < mid and left < right:
left += 1
alist[right] = alist[left]
# 循环一旦结束了,证明找到了mid应该在的位置
alist[left] = mid
# 递归操作
quick_sort(alist,start,left-1) # 这里不能用切片,因为切片会产生新的列表
quick_sort(alist,right+1, end)
if __name__ == "__main__":
alist = [5,3,4,7,2]
quick_sort(alist, 0, len(alist)-1)
print("排序后:",alist)
6.9 二分查找
# 二分查找算法
# 递归算法
def binary_search_re(alist,item):
"""二分查找"""
# 数列长度
n = len(alist)
# 递归条件的结束
if n == 0:
return False
# 找到中间值
mid = n//2
if item == alist[mid]:
return True
# 记住return不具有向上传递性
elif item < alist[mid]:
return binary_search_re(alist[0:mid], item)
elif item > alist[mid]:
return binary_search_re(alist[mid+1:], item)
def binary_search(alist, item):
"""二分查找"""
start = 0
end = len(alist) - 1
while start < end:
# 获取中间值
mid = (start + end)//2
if item == alist[mid]:
return True
elif item < alist[mid]:
end = mid - 1
elif item > alist[mid]:
start = mid + 1
return False
if __name__ == "__main__":
alist = [1,2,3,4,5]
print(binary_search(alist,3))
print(binary_search(alist,8))
print(binary_search_re(alist,4))
print(binary_search_re(alist,9))
6.10 广义二叉树的实现和4种遍历
# 实现完全2叉树
# None和Node易混淆,多注意
# 节点
class Node(object):
"""节点类"""
def __init__(self,item):
self.item = item
self.lchild = None
self.rchild = None
# 实现完全二叉树
class BinaryTree(object):
"""完全二叉树"""
def __init__(self, node=None):
self.root = node
def add(self,item):
"""添加节点"""
if self.root == None:
self.root = Node(item)
return
# 队列,
# 理解这个添加节点跟这个队列没有多大关系,队列只是一个辅助,
# 全部节点不在queue里存,它只是零时存中间的一些节点,节点知道头一个就行,就能知道剩下的
queue = []
# 从尾部添加数据
queue.append(self.root)
while True:
# 从头部取出数据,循环一次,往出取一个,
node = queue.pop(0)
# 判断左右节点是否为空,左节点是空了,就让它的左节点指向现在要添加的节点,添加了函数执行结束
if node.lchild == None:
node.lchild = Node(item)
# 添加后函数执行结束
return
# 如果左节点不为空,那就把左节点添加到队列中,因为等下要用这个左节点
else:
queue.append(node.lchild)
# 判断完左节点后,然后判断右节点,
if node.rchild == None:
node.rchild = Node(item)
return
else:
queue.append(node.rchild)
def breadh_travel(self):
"""广度优先遍历"""
# 如果之后理解不了广度优先遍历,那就再回头看看黑马的视频
# 如果没有节点
if self.root == None:
return
# 队列
queue = []
# 添加数据,知道了头就都知道了
queue.append(self.root)
while len(queue) > 0:
# 取出数据
node = queue.pop(0)
print(node.item, end="") # 不换行
# 判断左右节点是不是空
if node.lchild is not None:
# 把这个节点添加到队列中
queue.append(node.lchild)
if node.rchild is not None:
queue.append(node.rchild)
def preorder_travel(self, root):
"""先序遍历,根左右"""
if root is not None:
print(root.item, end="")
self.preorder_travel(root.lchild)
self.preorder_travel(root.rchild)
def inorder_travel(self, root):
"""先序遍历,左根右"""
if root is not None:
self.inorder_travel(root.lchild)
print(root.item, end="")
self.inorder_travel(root.rchild)
def postorder_travel(self, root):
"""先序遍历,左右根"""
if root is not None:
self.postorder_travel(root.lchild)
self.postorder_travel(root.rchild)
print(root.item, end="")
if __name__ == "__main__":
tree = BinaryTree()
tree.add("A")
tree.add("B")
tree.add("C")
tree.add("D")
tree.add("E")
tree.add("F")
tree.add("G")
tree.breadh_travel()
tree2 = BinaryTree()
tree2.add(0)
tree2.add(1)
tree2.add(2)
tree2.add(3)
tree2.add(4)
tree2.add(5)
tree2.add(6)
tree2.add(7)
tree2.add(8)
tree2.add(9)
print()
tree2.preorder_travel(tree2.root)
print()
tree2.inorder_travel(tree2.root)
print()
tree2.postorder_travel(tree2.root)
参考资料:
这篇博客讲的算法较多