22计算机408考研—数据结构—排序（详解加例题）

2022计算机考研408—数据结构—排序
手把手教学考研大纲范围内的排序
22考研大纲数据结构要求的是C/C++，笔者以前使用的都是Java，对于C++还很欠缺，
如有什么建议或者不足欢迎大佬评论区或者私信指出

Talk is cheap. Show me the code.
理论到处都有，代码加例题自己练习才能真的学会

文末投票：下篇22考研数据结构的博客写什么（欢迎评论区指出）

排序定义
冒泡排序
直接插入排序
二分插入排序
希尔排序⭐
快速排序
二路归并排序⭐
基数排序（附加计数排序）⭐
简单选择排序
堆排序⭐⭐

排序

排序的基本概念

顾名思义，给一个无序数组的值进行顺序存储

原数组：2 3 1 5 6 4 8 9 7
排序后：1 2 3 4 5 6 7 8 9

冒泡排序

思路：
从头到尾每两个相邻的元素，进行比较，前面的比后面的大就进行交换
循环一遍后，数组元素最大的就到了最后面，
第二次循环的时候，就可以不循环到最后一个了，最后一个上次循环已经是整个数组最大的值了
然后把这次最大的放到倒数第二个元素，
第三次循环的就可以忽略最后两个元素
以此类推，全部循环后，即可完成排序

#include 
#include 

using namespace std;


void bubbleSort(vector<int> &num);
int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    bubbleSort(num);    //调用自定义的排序方法
    cout << "排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void bubbleSort(vector<int> &num) {
    for (int i = 0; i < num.size(); i++) {
        for (int j = 0; j < num.size() - i; j++) {
            if (num[j] > num[j + 1]) {
//                int temp = num[j];
//                num[j] = num[j + 1];
//                num[j + 1] = temp;

                num[j] ^= num[j + 1];   //两两相邻交换   上面注释代码的功能与此功能相等
                num[j + 1] ^= num[j];
                num[j] ^= num[j + 1];


            }
        }
        
        //每次循环都把数组的变动输出出来
        for (int j = 0; j < num.size(); j++) {
            cout << num[j] << " ";
        }
        cout << "\n";
    }
}

//冒泡排序的变种

#include 
#include 

using namespace std;


void bubbleSort(vector<int> &num);
int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    bubbleSort(num);    //调用自定义的排序方法
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void bubbleSort(vector<int> &num) {
    int flag = 1;       //flag用来判断，如果本次循环没有进行交换，该数组为有序数组
    int arrBoundary  = num.size() - 1;  //用来记录上一次循环最后一次交换位置，后面没有交换的是有序的
    int largestSwapIndex = 0;           //记录最后一次交换的位置
    for (int i = 0; i < num.size(); i++) {
        flag = 1;
        for (int j = 0; j < arrBoundary ; j++) {
            if (num[j] > num[j + 1]) {
                int temp = num[j];
                num[j] = num[j + 1];
                num[j + 1] = temp;

                flag = 0;               //发生交换就改为0
                largestSwapIndex = j;   //交换位置就给largestSwapIndex
            }

        }
        arrBoundary = largestSwapIndex; //把当前循环交换的最后一个下标给arrBoundary
        if (flag) {     //如果本次循环没有交换任何值，证明当前数组为有序数组
            break;
        }
    }

}

直接插入排序

思路：
插入 == 把数插进去
也是两层循环
数组num

第一层循环从下标为1的值开始，循环变量为i
第二层循环就是把第一层的值拿出来，然后从第i-1个向前循环，找到第一个小于 num[i] 的值，
这个值的下标如果是j-1的话，那么 num[j] 就是第一个大于 num[i] 的值
把 num[i] 用一个变量 temp 保存一下
把下标为j到i-1的值依次向后移动一位，也就是说下标j到i-1的值移动到j+1到i，
然后把 temp(原num[i])放到下标为j的地方（之前的num[j]已经移动到num[j+1]了），

按照这种排序，每次循环的都是i之前的，i之前的元素都是顺序存储的，
文字表述的不清楚的可以看每次循环i更改后数组的元素情况

#include 
#include 

using namespace std;

void insertSort(vector<int> &num);
int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    insertSort(num);    //调用自定义的排序方法
    cout << "排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void insertSort(vector<int> &num) {
    for (int i = 1; i < num.size(); i++) {
        int temp = num[i];      //保存一下num[i]
        int j;
        //从num[j]向前开始找，一直找到比temp(原num[i])小的数就结束
        //在循环过程中的数都比temp大的，不断地把temp大的数往后移动一位
        //由此可得，等找到num[j]<=temp的时候，循环已经结束了
        // 但是他的上一个，也就是num[j+1]的值已经移动到num[j+2]了
        for (j = i - 1; j >= 0 && num[j] > temp; j--) {
            num[j + 1] = num[j];
        }
        //可以直接把temp放到num[j+1]，
        num[j + 1] = temp;
        //每次循环都可以把num[i]以及之前的数值排序好

        //每次循环都把数组的变动输出出来
        for(j = 0; j < num.size(); j++) {
            cout << num[j] << " ";
        }
        cout <<"\n";

    }
}

运行截图：

二分插入排序

思路：
二分插入和简单插入基本类似
不过是在寻找插入位置的时候不在采用简单插入的循环查找，而是使用二分查找
减少比较的次数，提升效率

#include 
#include 

using namespace std;

void binInsertSort(vector<int> &num);
int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    binInsertSort(num);    //调用自定义的排序方法
    cout << "排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void binInsertSort(vector<int> &num) {
    for (int i = 1; i < num.size(); i++) {
        int temp = num[i];          //保存临时变量
        int left = 0;               //使用二分法找到插入的位置left  使得num[left]
        int right = i - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (num[mid] > temp) {
                right = mid - 1;

            } else {
                left = mid + 1;
            }
        }
        for (int j = i - 1; j >= left; j--) {
            num[j + 1] = num[j];       //把left右面的值全部右移一位，
        }
        num[left] = temp;               //把temp放到num[left]的位置

        //每次循环都把数组的变动输出出来
        for (int j = 0; j < num.size(); j++) {
            cout << num[j] << " ";
        }
        cout << "\n";

    }
}

希尔排序

思路：

希尔排序其实可以看做是插入排序的变种
插入排序是循环到某个元素就像前找合适的位置，把当前元素到合适位置的值都要向后移动一遍
插入排序对于有序的数组，比较和移动的次数都比较少
希尔排序就是把插入排序进行分组化

分组是按照长度每次除2分的，这样最后一次肯定是一个组一个元素，就相当于最原始的插入排序了
而他前面做的按组排序就是为了让这个数组变成一个有大概顺序的数组，使后面的插入排序能减少比较和移动的次数

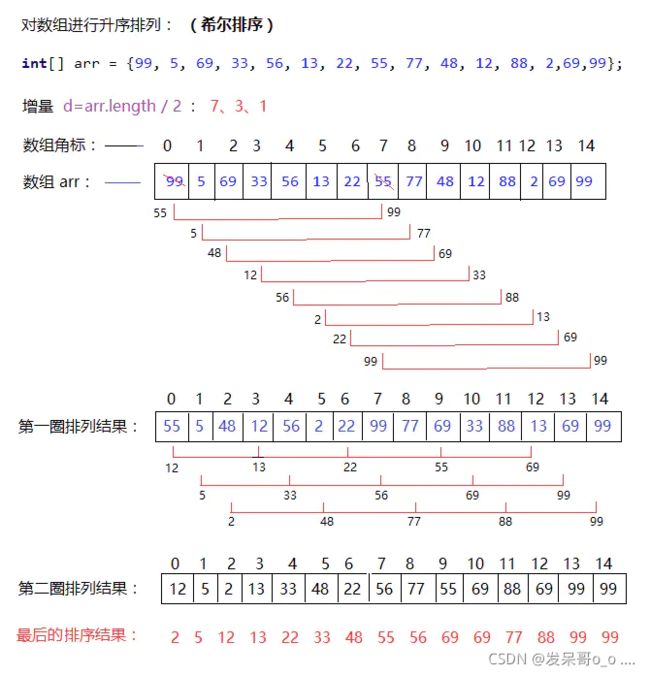
按下图为例子，数组长度15  第一次按照7个增量分组，第二次按照3个增量，第三次按照1个增量分组

第一次循环的增量为7
第一次是下标 0 与 0+7比较   1与1+7比较  ……   7 与 7+7比较
第一次循环完，这些位置上有了个大概的顺序

第二次循环的增量为3
第二次是下标 0与3与6与9与12比较   1与4与7与10与13   2与5与8与11与14
第二次循环完，这些位置上有了大概的顺序

第三次循环的增量为1
就相当于简单的插入排序

希尔排序的精髓就在于，对于一个大概有序的数组，插入排序的比较和移动次数都比较少

PS：小编作图能力有限，上图是当来的

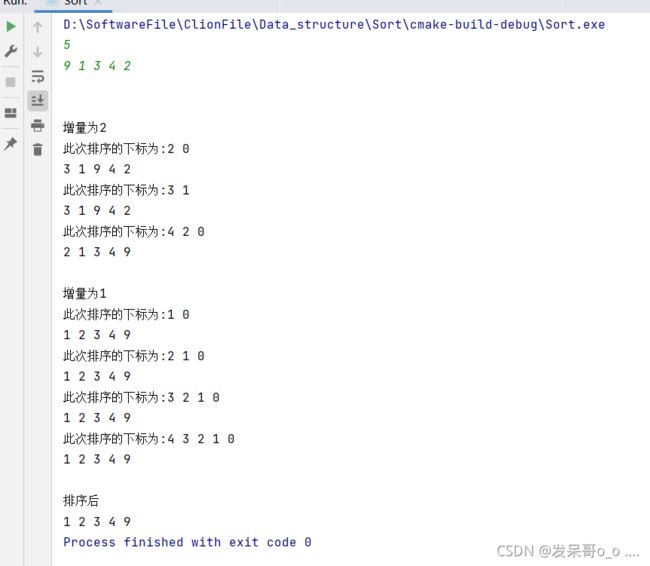
//除main方法外的其他cout输出都是为了让读者更清楚的了解每次循环后进行排序的下标
#include 
#include 

using namespace std;

void shellSort(vector<int> &num);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    shellSort(num);    //调用自定义的排序方法
    cout << "\n\n排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void shellSort(vector<int> &num) {
    int len = num.size();
    for (int d = len / 2; d > 0; d/=2) {    //按照增量分组，增量每次/2
        cout << "\n\n增量为" << d;
        for (int i = d; i < len; i++) {     //类似插入排序，每次都比较i之前的，
            cout << "\n此次排序的下标为:" << i;
            for (int j = i - d; j >=0; j-=d) {
                cout << " " << j;
                //这里i-d其实也就是从前面开始，
                // j每次都是j-=d，因为我们是按照相同增量分为一组的
                                                // 对比上图更容易理解
                if (num[j] > num[j + d]) {  //只要前面的比后面的大，就交换位置
                    int temp = num[j];
                    num[j] = num[j + d];
                    num[j + d] = temp;
                }
            }

            //每次循环都把数组的变动输出出来
            cout << "\n";
            for (int j = 0; j < num.size(); j++) {
                cout << num[j] << " ";
            }

        }
    }
}

快速排序

思路：
从未排序的数组中，一个一个的寻找，寻找当前值应该在排序后数组的位置，
以此类推，把每个值的位置都确定了以后，此数组就变成了排序后的数组
也是分段进行确定某个值最终排序后的下标

先选取第一个值，用一个临时变量保存这个值，然后双指针i表示这段范围的开头，j这段范围的结尾    
	j负责从后向前找小于临时变量的值，找到以后就把j的值放到i那，
		此时j位置就空出来了，我们当作把临时变量的值放到j这里
	i负责从前向后找大于临时变量的值，找到后就放到j那里，
		此时i位置就空出来了，我们同样当作把临时变量的值放到i这里
	不断循环这两步的操作，
	i是从前向后，j是从后向前
	循环结束的条件就是i==j  也就是临时变量排序后数组的位置，
	按照这种排序方式，结束后，
		比临时变量小的都在临时变量左边（左边不一定是排好序的），
		比临时变量大的都在临时变量右边（右边不一定是排好序的），
		也就是说临时变量当前的下标就是排序后的下标			
	
当前临时变量的位置确定好以后，我们可以分为前半部分和后半部分继续这种操作
以此类推，当每个值最终排序后的位置都确定的时候，此数组为排序后的数组		

下图为确定好一个值的最终位置的排序图

临时变量为50，左指针low，右指针high

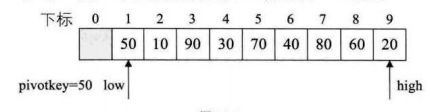
右指针找到20比临时变量小，交换两个值

左指针找到90比临时变量大，交换两个值

右指针找到40比临时变量小，交换两个值位置

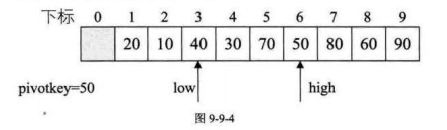
左指针找到70比临时变量小，交换两个值的位置

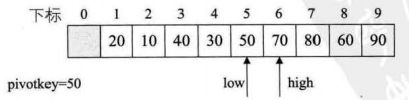
右指针左移与左指针重合，当前位置为50排序后的最终位置

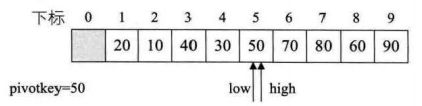
我们发现，左边的数都比50小，右边的数都比50大，
当前数的位置就是排序后当前数的位置 然后在把左边的数组按照这种方法，右边的数组按照这种方法
以此类推每个值的最终下标都确定下来了，数组为排序后的数组
PS：图仍然是某度当来的o(￣▽￣)ブ

#include 
#include 

using namespace std;


void quickSort(vector<int> &num, int left, int right);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    quickSort(num, 0, num.size() - 1);    //调用自定义的排序方法
    cout << "\n\n排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void quickSort(vector<int> &num, int left, int right) {
    if (left >= right) return;      //如果左节点>=右节点了，证明排序结束了，返回即可
    int temp = num[left];   //保存一下当前左节点的值，此次排序就是确定当前左节点的值
    int l = left;   //保存一下原始的左右边界
    int r = right;
    while (left < right) {      //循环的结束条件就是左指针 == 右指针，相等时就为temp排序后的最终位置
        while (left < right && temp < num[right]) { //右指针找比temp小的值，如果没找到就一直找
            right--;
        }
        if (left < right) {         //上面循环结束了就证明找到了，如果left == right，那么最终位置就确定好了，
            num[left] = num[right]; //然后把比temp小的放到左面left位置那里，然后left指向下一个值
            left++;                 //可能这里有些疑问，上面描述的是交换，这里没有交换，实际上每次都交换，换来换去，每次都重复换temp这个数
        }                           //不如直接赋值，然后把这个重复数直接放到最后确定的位置

        while (left < right && num[left] < temp) {  //这里是左指针找比temp大的数，找到就退出循环了，
            left++;
        }
        if (left < right) {     //与上面相反的道理，把比temp大的数放到right，right指针左移
            num[right] = num[left];
            right--;
        }
    }
    num[left] = temp;   //循环结束就是确定了temp最终的位置，左指针==右指针

    //每次循环都把数组的变动输出出来
    cout << "\n左边界下标:" << l << " 右边界下标:" << r << " 当前循环确定的下标为:" << left << "\n";
    for (int j = 0; j < num.size(); j++) {
        cout << num[j] << " ";
    }

    quickSort(num, l, left - 1);    //temp确定好了位置，把temp左面的数组和右面的数组分别进行这种方法排序
    quickSort(num, left + 1, r);    //当每个值的下标都确定的时候，该数组以完成排序
}

二路归并排序

思路：
二路归并，就是把一个数组，先分开，然后在合并的过程中逐步排序
二路就是分开的时候每次分成两个，分成两种路
归并就是把他分开在合上

二路分割数组，一直把数组分割到一路只有一个数为止
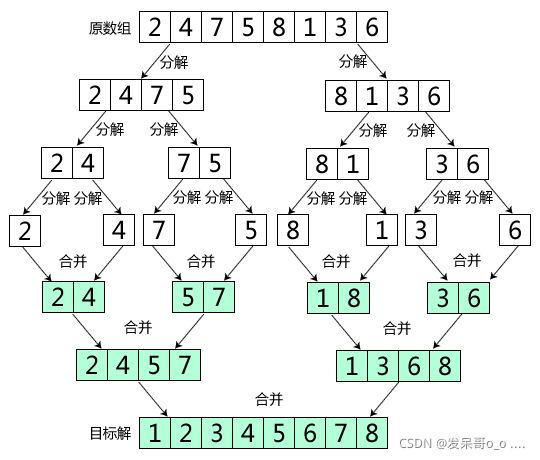
然后再把他们两路合一路，两路合一路，在合路的过程中把无序的路合成有序的路，慢慢的合成后的路都为有序的路，大致原理如下图

分路没有什么说的，一分为，对半分即可
合路的时候，AB两个路合成C路，分别两个指针i，j，k对应着A，B，C数组的下标
循环AB两个数组，每次都比较A[i]与B[j] 取两个数组中对应值小的放到C[k]
然后k下标右移，i或者j小的下标右移，完全循环后，C==A+B的有序路

#include 
#include 

using namespace std;

void mergeSort(vector<int> &num, int left, int right);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    mergeSort(num, 0, num.size() - 1);    //调用自定义的排序方法
    cout << "\n\n排序后" << endl;
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void mergeSort(vector<int> &num, int left, int right) {
    if (left == right) return;      //如果左节点和右节点相等，说明就分到底了，一路只剩下一个元素
    int m = (left + right) / 2;     //左节点和右节点的中间节点，从中间节点分路，左面一路，右面一路
    mergeSort(num, left, m);            //先分左面->左面进入后还会从上面再来，接着分，一直分到一路只有一个元素
    mergeSort(num, m + 1, right);   //再分右面
    //走到这里说明已经分完了，接下来就是合并
    int temp [right - left + 1];    //定义一个数组，用来存两路合并后的有序数组
    int l = left;                   //左路起始点下标
    int r = m + 1;                  //右路起始点下标
    int k = 0;                      //合路的起始点下标
    while (l <= m && r <= right) {  //每次放到时候比较对应的值，小的值放到前面，l要在左路的范围内，r要在右路的范围内
        if (num[l] <= num[r]) {     //谁小把谁放到合路
            temp[k++] = num[l++];
        } else {
            temp[k++] = num[r++];
        }
    }
    //下面两个while循环处理的是一路全部放进合路了，另一路没有完全放进，循环的作用就是把两路上面没放进去的全部放进去
    while (l <= m) {
        temp[k++] = num[l++];
    }
    while (r <= right) {
        temp[k++] = num[r++];
    }
    //temp就是我们合路，然后我们把合好的路放回到num原数组中
    for (int i = left, k = 0; i <= right; i++, k++) {
        num[i] = temp[k];
    }

    //每次循环都把数组的变动输出出来
    cout << "此次合并的是下标：" << left << "-" << right << "\n";
    for (int j = 0; j < num.size(); j++) {
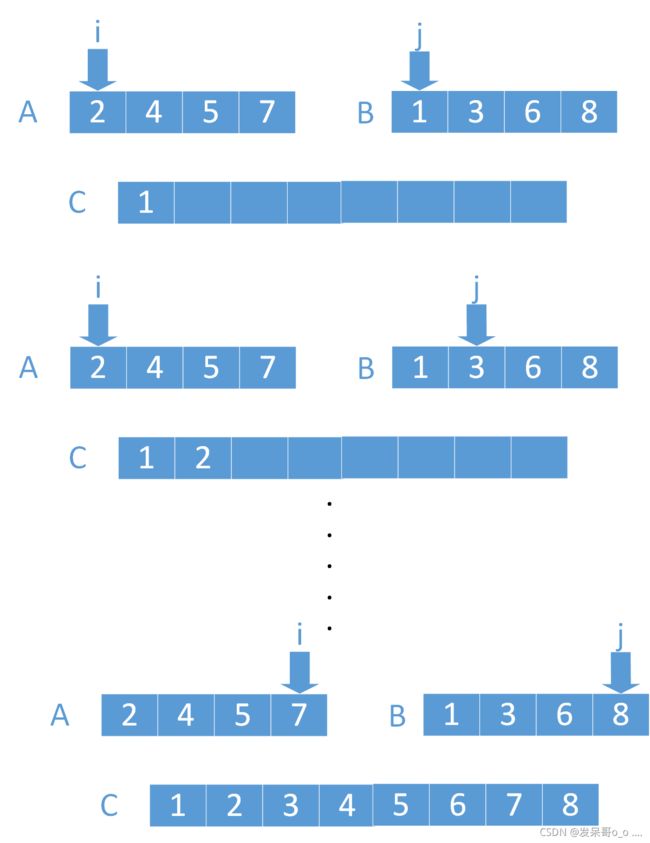
        cout << num[j] << " ";
    }
    cout << "\n";
}

Acwing，这个题就是归并排序
788. 逆序对的数量
  

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式
第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式
输出一个整数，表示逆序对的个数。

数据范围
1≤n≤100000，
数列中的元素的取值范围 [1,109]。

输入样例：
6
2 3 4 5 6 1
输出样例：
5





#include 
#include 

using namespace std;

void mergeSort(vector<int> &num, int left, int right);

int res = 0;
int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    mergeSort(num, 0, num.size() - 1);    //调用自定义的排序方法
     cout << res;
    return 0;
}

void mergeSort(vector<int> &num, int left, int right) {
    if (left == right) return;      //如果左节点和右节点相等，说明就分到底了，一路只剩下一个元素
    int m = (left + right) / 2;     //左节点和右节点的中间节点，从中间节点分路，左面一路，右面一路
    mergeSort(num, left, m);            //先分左面->左面进入后还会从上面再来，接着分，一直分到一路只有一个元素
    mergeSort(num, m + 1, right);   //再分右面
    //走到这里说明已经分完了，接下来就是合并
    int temp [right - left + 1];    //定义一个数组，用来存两路合并后的有序数组
    int l = left;                   //左路起始点下标
    int r = m + 1;                  //右路起始点下标
    int k = 0;                      //合路的起始点下标
    while (l <= m && r <= right) {  //每次放到时候比较对应的值，小的值放到前面，l要在左路的范围内，r要在右路的范围内
        if (num[l] <= num[r]) {     //谁小把谁放到合路
            temp[k++] = num[l++];
        } else {
            temp[k++] = num[r++];
            res += m - l + 1;   //当前l大于r证明l到m的数都大于r
                                //归并就是一段一段的排好序的数组合并起来的
        }
    }
    //下面两个while循环处理的是一路全部放进合路了，另一路没有完全放进，循环的作用就是把两路上面没放进去的全部放进去
    while (l <= m) {
        temp[k++] = num[l++];
    }
    while (r <= right) {
        temp[k++] = num[r++];
    }
    //temp就是我们合路，然后我们把合好的路放回到num原数组中
    for (int i = left, k = 0; i <= right; i++, k++) {
        num[i] = temp[k];
    }

}

基数排序

说基数排序之前，先大概说一下计数排序

计数排序

计数排序就是把元素的值当作下标使用，数量用那个下标对应的值记录
例如int num[]={5，2，1，4，3，2，1，2，6，4，1，2，5，2}
这样的数组我们就用计数排序
count的长度是上面数组的最大值-最小值+1或者最大值-最小值+1
循环上面的数组 count[num[i]]++;
到时候判断这个值存不存在，直接判断count[值]是否大于0
显而易见，计数排序的缺点就是如果数组中最大值很大，那么这个效率会很低

leetcode 计数排序例题
1122. 数组的相对排序
给你两个数组，arr1 和 arr2，

arr2 中的元素各不相同
arr2 中的每个元素都出现在 arr1 中
对 arr1 中的元素进行排序，使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。

 

示例：

输入：arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
输出：[2,2,2,1,4,3,3,9,6,7,19]
 

提示：

1 <= arr1.length, arr2.length <= 1000
0 <= arr1[i], arr2[i] <= 1000
arr2 中的元素 arr2[i] 各不相同
arr2 中的每个元素 arr2[i] 都出现在 arr1 中


class Solution {
    //arr2的数在arr1中一定出现
    //arr1的数不一定在arr2中有
    //arr2在arr1中出现过的数，按照arr2的相对顺序排列，arr1中剩下的数按照升序排在后面
public:
    vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
        int upper = *max_element(arr1.begin(), arr1.end());
        vector<int> count(upper + 1);
        //arr1中的数计数放到count
        for (int x: arr1) {
            ++count[x];
        }
        vector<int> ans;
        //如果arr1出现的数，arr2也出现了就输出
        //这样就是按照arr2的相对顺序输出
        for (int x: arr2) {
            for (int i = 0; i < count[x]; ++i) {
                ans.push_back(x);
            }
            //arr2出现的数字，就添加到ans里面，
            //添加过就把这个数字清零了，
            count[x] = 0;
        }
        //把剩下的未在arr2中出现的按照升序输出
        for (int x = 0; x <= upper; ++x) {
            for (int i = 0; i < count[x]; ++i) {
                ans.push_back(x);
            }
        }
        return ans;
    }
};

再回来说基数排序
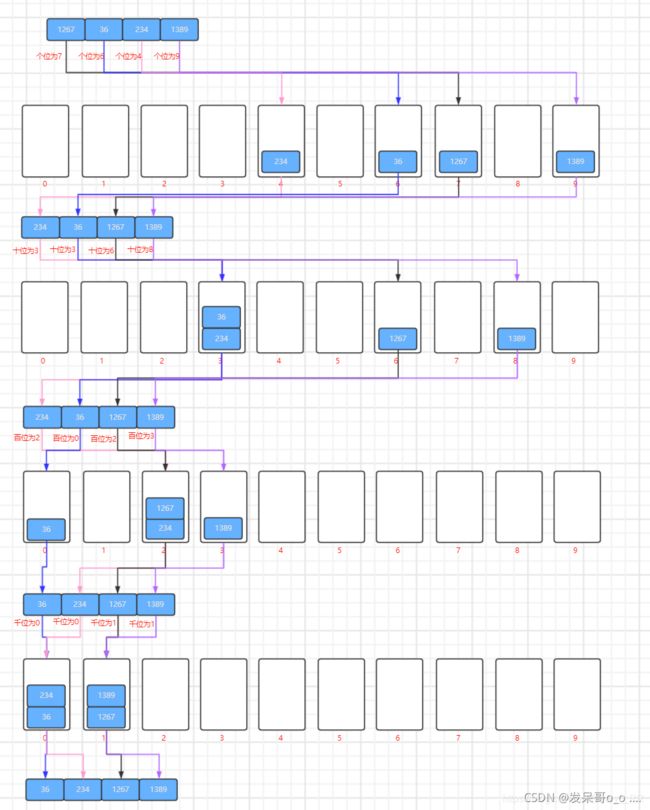
基数排序也是大概这个意思，不过不是直接把值当作下标，而是把值的每一位当作下标排序
这个也需要保存一下最大值，因为要判断最高有多少位。
先把个位放进去，排序，再把十位放进去排序，然后……

把个位放进去后，就按照个位排序好了，把数取出，记得按照顺序取出， 然后十位放进去排序，把数按顺序取出……
思路大概就是这样
顺序放入顺序取出，在进行下一位的排序
PS:
如果是Java的话，直接用一个ArrayList[] temp; 这种数组就可以

PS：当来的图片

#include 
#include 

using namespace std;

void radixSort(vector<int> &num);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    radixSort(num);    //调用自定义的排序方法
    cout << "\n\n排序后" << endl;
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void radixSort(vector<int> &num) {
    int max = -1;
    for (int i = 0; i < num.size(); i++) {
        max = max < num[i] ? num[i] : max;
    }
    int temp[num.size()];
    int count[10] = {0};
    for (int i = 0; i < num.size(); i++) {
        temp[i] = 0;                                    //初始化temp赋值0
    }

    for (int places = 1; places <= max; places *= 10) {     //基数排序就是按照位数进行排序，所以循环的次数就是数字位数

        for (int i = 0; i < num.size(); i++) {
            count[(num[i] / places) % 10]++;                  // 记录一下当前位上，各个数字的个数
        }                                                   //count[3]如果是5 就代表的个位为3的数是5个
        //当前位置上各个数字的个数确定了，我们就可以确定当前位某个数字的范围了
        //count[0] = 3, count[1] = 4, count[2] = 7, count[3] = 2……
        //当前位上为0的数在此次排序后的位置为数组1-3，当前位为1的数在此次位置为4-7，当前位为2的数的范围8-14……
        //也就是前面的和，加起来，得出的count[i] 就是当前位为i的数的范围的右边界
        for (int i = 1; i < 10; i++) {
            count[i] = count[i - 1] + count[i];
        }
        //因为我们上面count[i]得出的是当前位为i的时候的右边界，所以排序后的数组我们也应该从右面放
        //如果这里我们从左面开始放就会把放入的顺序弄反，我们已知右边界，然后把数字从右开始放顺序是正的
        //当然我们上一步也可以求每段范围的左边界，如果求得是左边界就可以从左放
        for (int i = num.size() - 1; i >= 0; i--) {
            int k = (num[i] / places) % 10;   //count[k]就是当前位为k的值的右边界
            temp[count[k] - 1] = num[i];    //这里的右边界我们用的是位置，下标要记得-1
            count[k]--;                     //当前位为k的数放进去后，count[k]要-1  因为已经放进去一个数了，右边界左移一位
        }
        //当所有的都循环完以后，count[i]代表的是当前位为i的数字范围的左边界
        for (int i = 0; i < 10; i++) {
            count[i] = 0;
        }
        //把此次排序的数组放到num中
        for (int i = 0; i < num.size(); i++) {
            num[i] = temp[i];
        }
        //输出展示此次排序后的数组
        cout << "\n哪一位是1，此次排序就是排的哪一位  " << places << "\n";
        for (int i = 0; i < num.size(); i++) {
            cout << num[i] << " ";
        }

    }

}

简单选择排序

思路：
简单选择排序，顾名思义，简单的选择一个元素排序
两层循环，第一层循环就是循环每一位
第二层循环，定义临时变量保存当前下标，循环后面每一位，
如果找到比当前下标对应的值小的，那么就用这个变量保存这个值小的下标，一直循环到结束
第一层循环结束后，变量保存的就是整个数组最小的值的下标，与第一位交换，第一位就是最小的值
如此往复，第二次循环，就从第二位开始向后找，记录除第一位最小的值的下标，循环结束后与第二位进行交换
以此类推，循环后即可完成排序。

#include 
#include 

using namespace std;


void selectSort(vector<int> &num);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    selectSort(num);    //调用自定义的排序方法
    cout << "排序后" << "\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void selectSort(vector<int> &num) {
    for (int i = 0; i < num.size(); i++) {      //循环每一位
        int temp = i;                           //保存当前位的下标
        for (int j = i + 1; j < num.size(); j++) {  //循环后面每一位，找到值比当前小的就保存值小的下标
            if (num[j] < num[temp]) {
                temp = j;
            }
        }
        int n = num[i];                         //temp保存的是i后面最小值的下标，与下标为i的值交换
        num[i] = num[temp];                     //如此往复，小的值到了前面，次小的到了第二位，……
        num[temp] = n;
        
        //每次循环都把数组的变动输出出来
        for (int j = 0; j < num.size(); j++) {
            cout << num[j] << " ";
        }
        cout << "\n";
    }
}

运行结果如下：

堆排序

思路：
首先要强调一下，堆排序并不是要构成一个堆，它本身还是个数组，只不过是我们在排序的时候把他看成一个堆，他实际上还是一个数组
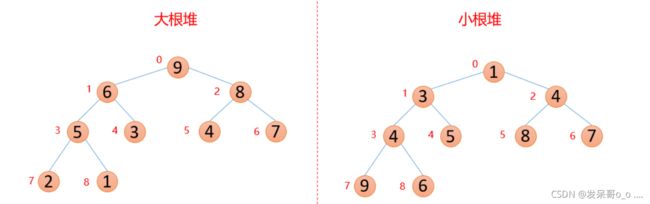
我们这里用到的堆是大根堆和小根堆，他们都是完全二叉树
完全二叉树就是他们结点位置和满二叉树的位置是一样的

红色角标为真实数组的下标

PS：图片来源
这是大根堆和小根堆

完全二叉树和满二叉树基本相同
每一层的数量都是上一层的二倍
某一层最左边结点下标*2就是最右边结点下标

完全二叉树中子结点和父结点之间还有一些显著的关系
一个数的下标为x
他的父节点下标为（x - 1）/ 2这里的除2是计算机除2，不保存余数，整除不成为小数
他的左子结点为 2 * x + 1
他的右子结点为 2 * x + 2

如果还不明白，可以自己带个结点试一下（看堆分析容易理解）
（左子结点-1）/2就是父节点 （右子结点 - 1）/2也是父节点，它除2的时候会把余数直接省去

大根堆就是 父节点 > 左子结点 并且 父节点 > 右子结点
小根堆就是 父节点 < 左子结点 并且 父节点 < 右子结点

构建大根堆只是思想构建，不是实际构建，实际还是数组
先把数组构建成大根堆，大根堆不一定是有序的，但一定是符合大根堆的规律，父结点一定比子结点大，全部构建好（构建大根堆，一定要从下向上构建，如果无序直接从上向下构建，有的会不符合大根堆定义）

默认叶子结点为排好序的堆（叶子结点没有子结点，只有一层，符合大跟堆得特征）
先添加非叶子结点，逐步向上添加
如果从上到下结点添加，叶子结点为有序堆，上到下添加会把有序堆打散，无法完成堆排序
完全二叉树的特点，n个结点，最后一个非叶子结点二叉树为（n/2）下标为（n/2-1），逐步向上添加

构建好大根堆后，转换成小根堆

转换小根堆的步骤，先把大根堆最大的（也就是堆顶）与最后面的结点换位置，这样能保证最大的在最后面，也就是说，数组第一位与最后一位交换
交换完，小的就到了最上面，把刚交换完最大的固定不动，其他的重新构建大根堆
此时最大的在最后面，其他的仍然是大根堆

第二次的时候，把当前大根堆最大的值（当前堆顶）与倒数第二位交换（倒数第一位是刚才的堆顶，最大的，已经固定了，保持不变），最小的又到了堆顶，继续重建大根堆
如此往复，大根堆就变成了小根堆，此时的小根堆就是有序的

#include 
#include 

using namespace std;

void heapSort(vector<int> &num);

void heapBuild(vector<int> &num, int fatherIndex, int len);

int main() {
    int n;    //n为将要输入的数组长度
    cin >> n;   //输入n   cin方法需要上面使用std
    vector<int> num;    //定义vector  记得上面导入vector
    int temp;   //temp为输入vector时的中间变量
    for (int i = 0; i < n; i++) {
        cin >> temp;            //输入
        num.push_back(temp);
    }
    heapSort(num);    //调用自定义的排序方法
    cout << "\n\n排序后" << endl;
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";     //输出
    }
    return 0;
}

void heapSort(vector<int> &num) {
    //构建大根堆
    for (int i = num.size() / 2 - 1; i >= 0; i--) { // 倒数第二排开始, 创建大顶堆，必须从下往上比较
        heapBuild(num, i, num.size());                 // 否则有的不符合大顶堆定义
    }
    cout << "构建完大根堆后的数组\n";
    for (int i = 0; i < num.size(); i++) {
        cout << num[i] << " ";
    }
    int len = num.size();
    //也算一种选择排序，因为每次把大根放到最后就少排序一个
    while (len > 1) {
        //每次都把大根与最后面的值交换，
        int temp = num[0];
        num[0] = num[len - 1];
        num[len - 1] = temp;
        len--;  //最后一个元素也就是刚才的大根已经确定好了，可以少排序一个元素
        heapBuild(num, 0, len);  //除去确定好的大根，把剩下的元素重新构建
        cout << "\n下标："<< len << " 值：" << num[len] <<" 确定好位置了\n";
        for (int i = 0; i < num.size(); i++) {
            cout << num[i] << " ";
        }
    }
}



void heapBuild(vector<int> &num, int fatherIndex, int len) {
    //堆（完全二叉树）左子结点和右子结点与父结点的关系
    int left = fatherIndex * 2 + 1;
    int right = fatherIndex * 2 + 2;
    while (left < len) {
        int largestIndex;   //largestIndex保存的是当前子结点与父结点中最大的索引
        if (num[left] < num[right] && right < len) {
            largestIndex = right;
        } else {
            largestIndex = left;
        }
        if (num[largestIndex] < num[fatherIndex]) { //如果父节点大于子结点，当前符合大根堆,退出即可
            largestIndex = fatherIndex;
            break;
        }
        //不符合大根堆就交换
        int temp = num[largestIndex];
        num[largestIndex] = num[fatherIndex];
        num[fatherIndex] = temp;
        //接着去下面构建大根堆
        fatherIndex = largestIndex;
        left = fatherIndex * 2 + 1;
        right = fatherIndex * 2 + 2;
    }
}