An Algorithm of Simulation of Fog with Different Visibility
作者:
- Cuimin Sun1,Department of Automation University of Science and Technology of China
- Bin Kong,Lixin He and Qiang Tian,Institute of Intelligent Machine,Chinese Academy of Science University of Science and Technology of China
Abstract
在本文中,作者提出了一个基于单幅输入图像的不同能见度的雾成像仿真算法,该算法适用于远景和近景图像,简单有效。主要包括三个步骤:
1.首先在单幅图像中获取散焦图(defocus map),然后根据镜头成像原理将其转换为深度图;
2.利用相关方程将深度图转换为透射率图;
3.通过大气散射模型生成雾模拟图像
Introduction
在此部分作者在气象学角度对雾的形成作了解释,由于雾霾的存在,图像的亮度、对比度、分辨率会大大降低。当前有关雾霾的研究热点在于从图像中去除雾霾影响,恢复高质量的无雾图像。为了检查雾中系统的鲁棒性,需要模拟雾中的场景成像,也就是在图像中添加雾化效果,使其看起来像真实的雾霾场景。雾霾仿真的研究方法主要有两种:
1.基于MTF建立雾的模型
MTF是雾在大气中传播的光学传递函数(optical transfer function),但是由于大气成分复杂,还停留在理论层面,难以实际应用。
2.使用蒙特卡洛方法(Monte Carlo's method)直接求取辐射传递方程
这种方法也称为统计模拟方法,主要思想是用伪随机数解决问题,处理过程的计算量巨大,耗费时间[5]。
[5] Dumont E. Caractérisation, modélisation et simulation des effets visuels du brouillard pour l'usager de la route [PhD Thesis]. France: Univ. of Paris V,2002.
Mohamed Benjamaa在2008年使用该方法合成了雾天驾驶道路的现场照片[6],他的算法降低了计算复杂度,建立了天空亮度和表面反射的模型。但是这种模型仅仅测试了白天行车道路的雾成像模拟,并且是基于雾霾成分均匀的假设,这显然是不符实际的。
[6] Benjamaa M., RozéC., Grasole T., Meyzonnette J.L., Lavergne C.
Digital image computation of scenes during daytime fog [J]. Optical Engineering. 47(3):037401,2008.
因此,后面的许多学者尝试对其进行改进,最常用的就是Deirmendjian提出的改进γ-分布模型[7]
[7] Deirmendjian D. Electromagnetic Scattering on Spherical Polydispersions. Santa Monica, CA: RAND Corporation,1969.
雾霾成像仿真的技术瓶颈在于图像场景深度的获取,因为大气透射率的求取需要场景深度。我们当然可以利用诸如
1.雷达、激光测距仪等精密设备,
2.或者通过具有不同角度
3.或者具有相同角度但退化程度不同的照片
来获取深度图,但显然这些方法操作性不高。
在卓少杰[9]的论文中,提出了一种新方法,这种方法通过从边缘位置向整个图像传播一种散焦模糊估计,从而获得完整散焦图。
本文就是利用卓少杰的方法获取散焦图,然后根据薄透镜理论将其转换为深度图,然后将其输入到大气散射模型中获取雾化图像。
[9] Shaojie Zhuo,TerenceSim,Defocus map estimation from a single image,Pattern Recognition 44pp. 1852–1858,2011.
Algorithm Introduced
A.基于从单个图像恢复的散焦图的深度估计
输入图像的深度图是雾成像模拟的前提。根据卓少杰提出的方法,可以从单个图像中恢复散焦图。
主要思想是使用已知的高斯核对输入图像进行模糊处理,并可以根据输入图像与模糊图像之间的梯度之比估算输入图像的散焦模糊量[9]。
再根据镜头成像将散焦图转换为深度图[11] :
其中,是图像每点的深度,是散光圈,指的是图像中每一点的散焦量,是焦距,是光圈值。
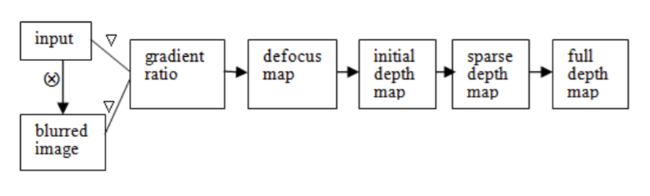
由于噪声的影响,初始深度图不够准确,需要对其进行滤波以获得稀疏深度图,然后通过插值获得完整的深度图。具体过程如图1所示。
在此,和分别表示卷积和梯度化,经过此操作后的深度图边缘清晰,连续性好。
B.透射图
透射率图描述光在传播过程中的衰减程度,它与深度图的数学关系如下:
其中,是透射率图, 是深度图, 是代表大气散射系数,表示单位体积的空气在所有方向上的光散射能力。
再根据光在随机介质中的传播理论[11],可以表示为:
其中是最大可视距离。
[11] Wu Jian,Le Shixiao,The light propagation theory in random medium[M],Chengdou,Chengdu telecom engineering college press,1988.
C.大气散射模型
大气散射模型是一种简单的物理模型,广泛应用于视觉图像和视觉研究。根据雾天条件下光学传输的物理特性,Nayar[10]提出了假设雾天分布均匀的大气散射雾天双色成像模型。数学表达式是:
其中为成像设备捕获的衰减图像,为等效全球大气光,为无衰减的场景图像,相当于无雾场景图像。
D.基于单幅图像的雾成像仿真算法
基于以上分析,设计出一个雾成像仿真算法,流程如下:
1.利用卓少杰的方法,从单幅输入图像中生成边缘到中心的渐变离焦模糊图像,然后通过计算输入图像的梯度与模糊图像的比值来估计输入图像的离焦量;
2.根据输入图像的离焦信息,根据透镜成像理论计算每个点的深度,生成初始深度图;
3.为了减小噪声的影响,对初始深度图进行滤波得到稀疏深度图,然后通过深度插值将其转换为全深度图;
4.利用公式(2)和散射系数计算出不同距离下的能见距离;
5.将深度图和散射系数代入公式(3)获得透光率图;
6.利用公式(4),最终生成雾模拟图像。这里,初始输入图像被用作。
这个算法最重要的步骤就是深度图的获取和大气光值的估算。
Experiment results and analysis
为了验证该算法的有效性,进行了具有远景图像输入的雾场仿真。仿真的关键步骤是从单输入图像中获取深度图。关键步骤流程如下:
1.首先,使用高斯核对输入图像(图a)进行散焦模糊处理,将标准偏差设置为1.5,然后分别计算输入和模糊图像的梯度,结果如图b和c图所示。
2.接下来,基于输入图像和散焦模糊图像梯度之间的比率的计算,估计输入图像的散焦量,然后生成初始深度图,为降低噪声,将其过滤为稀疏深度图(图d)。
4.最后,通过深度插值[12]得到全深度图,如图e所示。
强度越大,表示本文所有深度图的深度越大。
在得到全深度图后,利用大气散射模型进行仿真实验,在实验中,最大可见距离分别设置为300m、500m、800m,根据公式(2)、(3)、(4)求出散射系数、透射率图、仿真图像,是三维矢量,代表大气光的RGB值,在此被设置为(200,200,200)。
Conclusion
在上一部分分别用远观和近观照片对所提出的算法进行了测试,完成了雾天场景在不同能见度水平下的成像模拟。模拟结果符合大气散射和空间透射原理。在模拟图像中,从近到远,雾由薄到厚;当能见度降低时,雾的密度增大,远处景物的清晰度比近处景物差得多。这些现象都符合自然规律,使得仿真结果自然逼真。实验证明,该算法既适用于远距离场景,也适用于近距离场景,是一种简单而有效的雾场仿真方法。
但是这个算法并不完美。缺点之一是假设在相同场景深度下,雾的密度是相同的。在现实生活中,雾的形态和密度是复杂的、不规则的,在同一场景深度下雾的密度并不总是均匀的。如何在算法中加入更多的雾的细节,使仿真结果更加真实是下一步的工作。