【数据挖掘时间序列分析】餐厅销量预测
餐厅销量预测
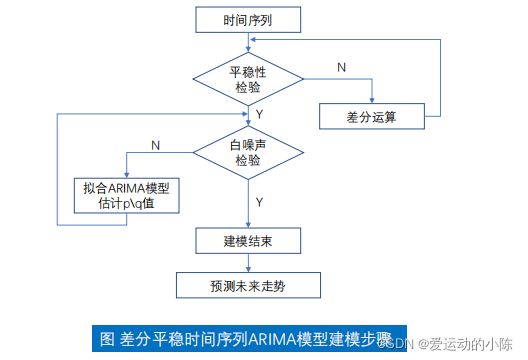
- 一、建模流程
- 二、模型简介
-
- 2.ARIMA模型介绍
-
- 2.1自回归模型AR
- 2.2移动平均模型MA
- 2.3自回归移动平均模型ARMA
- 三、模型识别
- 四、模型检验
-
- 4.1半稳性检验
-
- (1)用途
- (1)什么是平稳序列?
- (2)检验平稳性
- ◆白噪声检验(纯随机性检验)
-
- (1)用途
- (1)什么是纯随机序列?
- (2)检验纯随机性
- 五、Python实战
-
- (一)导入工具及数据
- (二)原始序列的检验
- (三)一阶差分序列的检验
- (四)定阶(参数调优)
- (五)建模与预测
一、建模流程
二、模型简介
2.ARIMA模型介绍
2.1自回归模型AR
自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
自回归模型首先需要确定一个阶数p,表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为:
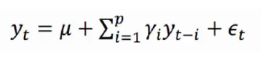 上式中yt是当前值,u是常数项,p是阶数 ri是自相关系数,et是误差。
上式中yt是当前值,u是常数项,p是阶数 ri是自相关系数,et是误差。
自回归模型有很多的限制:
1、自回归模型是用自身的数据进行预测
2、时间序列数据必须具有平稳性
3、自回归只适用于预测与自身前期相关的现象
2.2移动平均模型MA
移动平均模型关注的是自回归模型中的误差项的累加 ,移动平均法能有效地消除预测中的随机波动,q阶自回归过程的公式定义如下:
![]()
2.3自回归移动平均模型ARMA
自回归模型AR和移动平均模型MA模型相结合,我们就得到了自回归移动平均模型ARMA(p,q),计算公式如下:
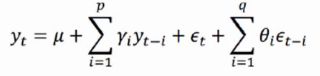
三、模型识别
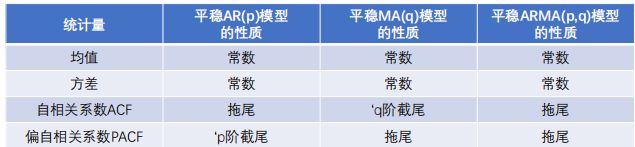
自相关函数ACF:时间序列观测值与其过去的观测值之间的线性相关性。
偏自相关函数PACF:在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性
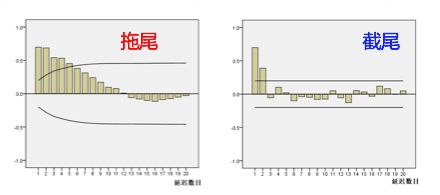
拖尾和截尾
拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小:
四、模型检验
4.1半稳性检验
(1)用途
建模之前,检验时间序列数据是否满足平稳性,才能进-步建模
(1)什么是平稳序列?
如果时间序列在某-常数附件波动且波 动范围有限,数学表达即常数均值和常数方差,并且延迟k期的序列变量的自协方差和自相关系数是相等的,则称该序列为平稳序列。
(2)检验平稳性
方法一:图检验(偏主观)
时序图检验:在某-常数附近波动且波动范围有限。
自相关图检验:平稳序列具有短期相关性,但随着延迟期数k的增加,自相关系数会快速衰减趋向于零。
方法二:单位根检验
不存在单位根即是平稳序列。
◆白噪声检验(纯随机性检验)
(1)用途
建模之前,检验数据是否满足白噪声检验,非白噪声才能进一步建模。
建模后,检验残差是否满足白噪声检验,通过检验,建模才成立。
(1)什么是纯随机序列?
如果-个序例是纯随机序列,那么序列值之间没有任何关系,则自相关系数为零(理论)或接近于零(实际) .
(2)检验纯随机性
方法- -:图检验
自相关图检验:自相关系数为零或接近于零
QQ图检验:大部分点在直线上,则数据符合正态分布
方法二: D-W检验或L .B统计量检验
五、Python实战
(一)导入工具及数据
#导入数据
sale=pd.read_excel("C://Python//分享资料2//arima_data.xls")
print(sale.head())
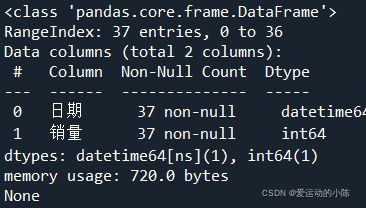
print(sale.info())
(二)原始序列的检验
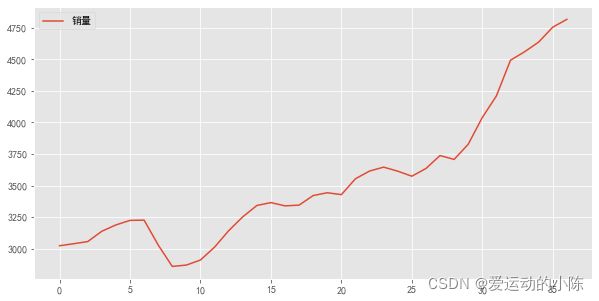
#时序图观看是否平稳序列
plt.figure(figsize=(10,5))
sale['销量'].plot()
plt.legend(['销量'])
plt.show()
自相关图
# 查看自相关图
sale['销量']=sale['销量'].astype('float')
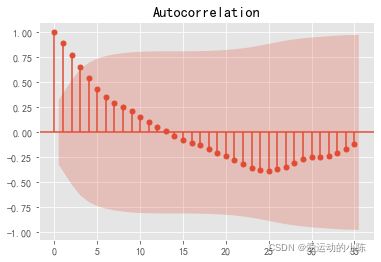
plot_acf(sale['销量'],lags=35).show()
#解读:自相关系数长期大于零,没有趋向于零,说明序列间具有很强的长期相关性。
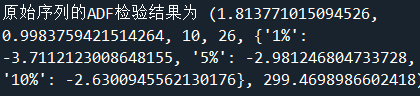
print('原始序列的ADF检验结果为',ADF(sale['销量']))
#解读:P值(第二个)大于显著性水平α(0.05),接受原假设(非平稳序列),说明原始序列是非平稳序列。
(三)一阶差分序列的检验
#方法:单位根检验
# print('原始序列的ADF检验结果为',ADF(sale['销量']))
d1_sale=sale.diff(periods=1, axis=0).dropna()
d1_sale=d1_sale['销量']
#时序图
plt.figure(figsize=(10,5))
d1_sale.plot()
plt.show()
#解读:在均值附件比较平稳波动
#自相关图
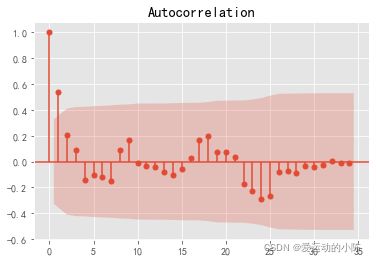
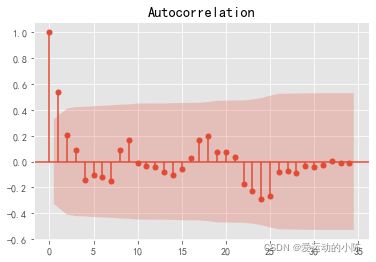
plot_acf(d1_sale,lags=34).show()
#解读:有短期相关性,但趋向于零。
#平稳性检验
print('原始序列的ADF检验结果为:',ADF(d1_sale))
#解读:P值小于显著性水平α(0.05),拒绝原假设(非平稳序列),说明一阶差分序列是平稳序列。

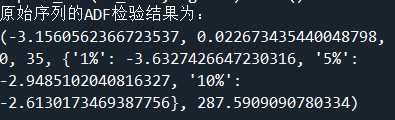
平稳性检验ADF小于0.05,说明一阶差分是平稳的
白噪声检验
print('一阶差分序列的白噪声检验结果为:',acorr_ljungbox(d1_sale,lags=1))#返回统计量、P值
#解读:p值小于0.05,拒绝原假设(纯随机序列),说明一阶差分序列是非白噪声。

p值小于0.05,拒绝原假设(纯随机序列),说明一阶差分序列是非白噪声。
(四)定阶(参数调优)
确定P值和Q值
# 参数调优:BIC
# # 模型调优的方法:AIC和BIC
# # 值越小越好
# # 参数调优的方法非常多,用不同方法得出的结论可能不同
# from pandas.core.frame import DataFrame
# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# bic_matrix=[]
# for p in range(pmax+1):
# tmp=[]
# for q in range(qmax+1):
# try:
# tmp.append(ARIMA(sale,(p,1,q)).fit().bic)
# except:
# tmp.append(None)
# bic_matrix.append(tmp)
# p,q=DataFrame(bic_matrix).stack().idxmin() #最小值的索引
# print('用BIC方法得到最优的p值是%d,q值是%d'%(p,q))
# pmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# qmax=int(len(d1_sale)/10) #一般阶数不超过length/10
# aic_matrix=[]
# for p in range(pmax+1):
# tmp=[]
# for q in range(qmax+1):
# try:
# tmp.append(ARIMA(sale,(p,1,q)).fit().aic)
# except:
# tmp.append(None)
# aic_matrix.append(tmp)
# aic_matrix=pd.DataFrame(aic_matrix)
# p,q=aic_matrix.stack().idxmin() #最小值的索引
# print('用AIC方法得到最优的p值是%d,q值是%d'%(p,q))
用AIC和BIC方法得到的最优的P值和Q值为0,1
(五)建模与预测
#构建模型
model=ARIMA(sale['销量'],(0,1,1)).fit()
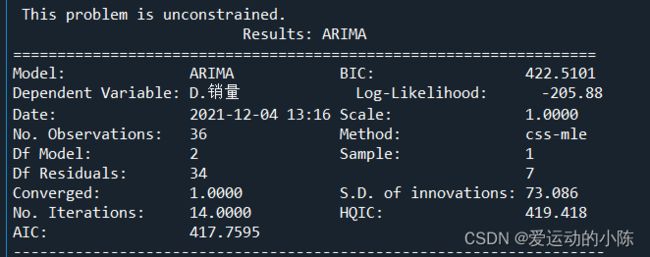
#查看模型报告
print(model.summary2())
#残差检验
#自相关图
resid=model.resid
plot_acf(resid,lags=35).show()
#解读:有短期相关性,但趋向于零。
#偏自相关图
plot_pacf(resid,lags=20).show()
#偏自相关图
plot_pacf(resid,lags=35).show()
#
如图所示一阶,二阶,三阶都是非常小的数,说明它们之间的相关性比较小,可能是一个纯随机序列
#qq图:线性即正态分布
qqplot(resid, line='q', fit=True).show()
#解读:残差服从正态分布,均值为零,方差为常数
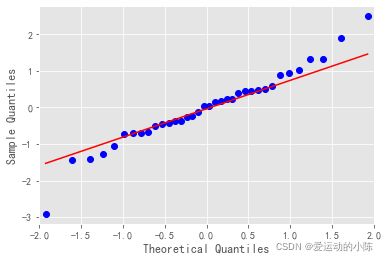
上图可以看出数据均匀的落在直线的周围,说明数据服从正态分布:均值为0,方差为常数,是一个纯随机序列。
预测
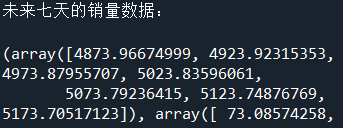
print('未来七天的销量数据:\n')
print(model.forecast(7))
#预测
# print('未来七天的销量数据:\n')
# print(model.forecast(7))
forecast=pd.Series(model.forecast(7)[0],index=pd.date_range('2015-2-7',periods=7,freq='D'))
data=pd.concat((sale,forecast),axis=0)
data.columns=['日期','销量','未来7天销量']
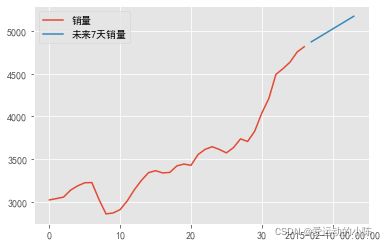
plt.figure(figsize=(10,5))
data[['销量','未来7天销量']].plot()
plt.show()