概率机器人：测距传感器的波束模型

机器人感知

测量模型

测量模型：用于描述客观世界中生成传感器测量数据的过程。

模型的特性取决于传感器：

• 成像传感器 ：通过投影几何学建立
• 声纳传感器 ：通过描述声波和声波在环境表面上的反射建立

测量模型定义为一个条件概率密度$p(z_t|x_t,m)$，表示在环境地图$m$和机器人位姿为$x_t$的条件下，传感器测量得到$z_t$的概率密度。

传感器在进行测量时，将会产生一系列的测量值。如相机传感器返回一组完整的数据（亮度、饱和度、色彩）；同样，测距传感器将产生一些列测距值，其中每个$z_t^k$表示一个独立的测距值：
$$z_t=\{z_t^1,z_t^2,\cdots ,z_t^K\}$$
对每个独立的测量相乘可以得到测量模型：
$$p(z_t|x_t,m)=\prod _{K=1}^{K}p(z_t^K|x_t,m)$$
理想条件下，每个独立测量束噪声之间相互独立，符合马尔可夫假设。

地图

环境的地图（map）给出了环境中物体的列表及其属性，包含特征地图和位置地图两大类。

基于特征的地图

在基于特征的地图（Feature-based Maps）中，用下标$n$表示特征索引，N表示环境中物体的总数：
$$m=\{m_1,m_2,\cdots ,m_N\}$$
每个$m_n(1\le n\le N)$指定一个属性，包含了特征的属性及特征的笛卡尔位置。

基于特征的地图仅指明在指定位置（即地图中包含的对象的位置）的环境的形状，特征描述法使得调节对象的位置更为简单。

基于位置的地图

在基于位置的地图（Location-based Maps）中，用下标$x,y$表示平面地图中，该物体的坐标：
$$m=\{m_{0,0},m_{0,1},\cdots ,m_{x,y}\}$$
每个$m_{x,y}$指定为平面坐标为$(x,y)$的属性。

基于位置的地图具有体积（volumetric），体积地图不仅包含环境物体的信息，也包含了对象没有物体的信息（即闲置区域)

占用栅格地图

占用栅格地图（Occupancy Grid Map）是一种经典的地图表示法，它是基于位置的地图。

占用栅格地图为每一个坐标$(x,y)$分配了一个二值占用值，用于指明该位置是否被某个对象占用。被占用的区域称为占用区域，未被占用的区域称为闲置区域。

占用栅格地图使得搜寻机器人通过闲置区域抵达目标点的路径更为便捷。

测距仪的波束模型

测距仪测量到附近物体的距离，可沿着一个波束测量（激光测距仪优选模型）或在一个测量锥内测量（超声波传感器优选模型）。

模型建立

测距仪的波束模型（Beam Model）$p(z_t|x_t,m)$可以看作是四种在机器人移动过程中存在的噪声的混合，每类噪声代表一种在实际运行中测距仪误差的产生。

噪声一：测量噪声模型

理想情况下，测距仪总是测量位于其测量范围内最近物体的实际距离$z_t^{k\ast }$。但由于测距传感器受到环境噪声影响，所得返回值一般为测量值$z_t^k$。在不同的地图中，可采用不同方式得到实际距离：

• 基于位置的地图：射线投影法
• 基于特征的地图：在测量锥内寻找最近特征以获取

通常采用均值为$z_t^{k\ast }$，标准差为${\sigma }_{hit}$的高斯分布来建模该噪声，如图所示采用$p_{hit}$表示此概率密度：

由于测距传感器存在测量最大值$z_{max}$，同时测量值必定大于等于零，则给定测量噪声表达式：
$$p_{hit}(z_t|x_t,m)=\{\begin{array}{ll}\eta \mathcal{N}(z_t^k;z_t^{k\ast },{\sigma }_{hit}^2)& 0\le z_t^k\le z_{max}\\ 0& 其他\end{array}$$
式中，实际距离$z_t^{k\ast }$由射线投影计算得到；$\mathcal{N}(z_t^k;z_t^{k\ast },{\sigma }_{hit}^2)$表示均值为$z_t^{k\ast }$，方差为${\sigma }_{hit}^2$的关于变量$z_t^k$的正态分布：
$$\mathcal{N}(z_t^k;z_t^{k\ast },{\sigma }_{hit}^2)=\frac{1}{\sqrt{2\pi {\sigma }_{hit}^2}}exp(-\frac{1}{2}\frac{(z_t^k-z_t^{k\ast }{)}^2}{{\sigma }_{hit}^2})$$
$\eta$为归一化因子：
$$\eta =({\int }_0^{z_{max}}\mathcal{N}(z_t^k;z_t^{k\ast },{\sigma }_{hit}^2)d{z}_t^k{)}^{-1}$$
噪声的标准差${\sigma }_{hit}$为测量模型的固有参数。

噪声二：环境噪声模型

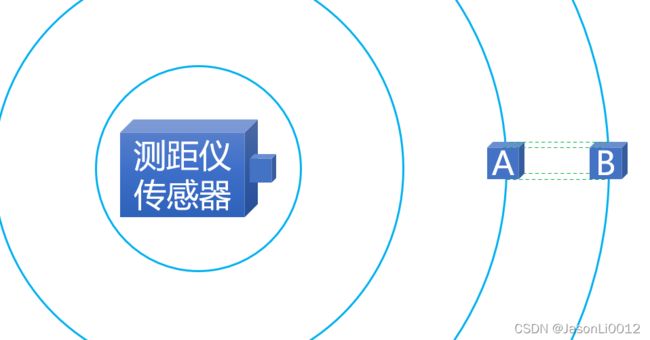
由于地图信息$m$为静态信息而机器人移动环境为动态环境，当实际环境内存在地图信息中不包含的对象时（如建图时，环境内不包含操控机器人的人物所处信息），测距仪将受到意外环境噪声影响。从而将导致实际距离$z_t^{k\ast }$更短。

此类意外对象造成测距仪噪声的可能性随着其距离而概率降低。如图所示，由于测距仪返回距离其最近的物体的距离，此时意外对象A和B出现在地图环境内，且A位于B前侧，则唯有A不出现时，测距仪能够感测到意外对象B的存在，否则仅传回意外对象A存在。

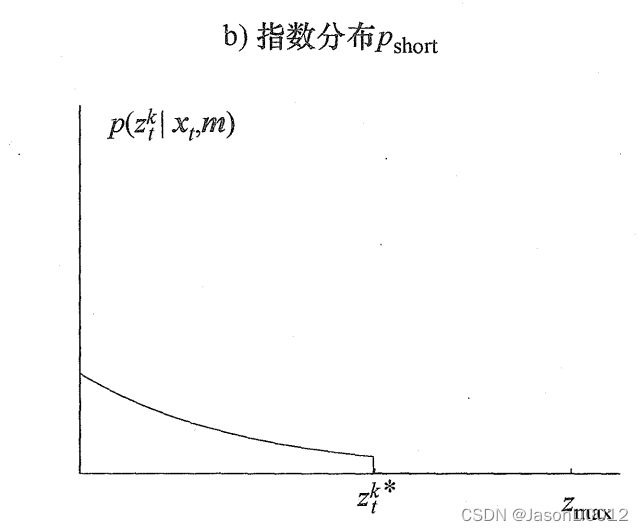
由此，采用指数分布来建模此类噪声现象，如图所示，采用$p_{short}$表示指数分布噪声：

在定义域范围内，模型如下所示：
$$p_{short}(z_t|x_t,m)=\{\begin{array}{ll}\eta {\lambda }_{short}exp(-{\lambda }_{short}\cdot z_t^k)& 0\le z_t^k\le z_t^{k,\ast }\\ 0& 其他\end{array}$$
式中，参量${\lambda }_{short}$为模型的固有参量；$\eta$为归一化因子：
$$\begin{array}{rl}\eta & =({\int }_0^{z_t^{k\ast }}{\lambda }_{short}exp(-{\lambda }_{short}\cdot z_t^k)d{z}_t^k{)}^{-1}\\ & =（-exp(-{\lambda }_{short}{z}_t^{k\ast })+exp(-{\lambda }_{short}0){）}^{-1}\\ & =\frac{1}{1-exp(-{\lambda }_{short}{z}_t^{k\ast })}\end{array}$$

噪声三：失败噪声模型

当所处环境存在镜面类容易反射激光束、声纳等信号的环境，或激光测距仪检测到黑色吸光现象、高光照下激光测量失败等情况时，环境存在测量失败噪声。

此时，测距仪将返回传感器的最大允许范围值$z_{max}$。采用以$z_{max}$为中心的点群分布建模，以$p_{max}$表示该模型：

实际上，$p_{max}$为一个离散分布，上图将其用一个很窄的以$z_{max}$为中心的均匀分布给出，则模型的数学表达式如下所示：
$$p_{max}(z_t^k|x_t,m)=I(z=z_{max})=\{\begin{array}{ll}1& z=z_{max}\\ 0& 其他\end{array}$$
式中，函数$I(z=z_{max})$为指示函数，当括号内条件成立时返回1，其余返回0。

噪声四：随机噪声模型

此外，测距仪传感器可能偶尔存在无法解释的测量，将其简化为在测量区间$[0,z_{max})$中存在一个均匀分布，如图所示，定义为$p_{rand}$：

$$p_{rand}(z_t^k|x_t,m)=\{\begin{array}{ll}\frac{1}{z_{max}}& 0\le z_t^k<z_{max}\\ 0& 其他\end{array}$$

波束模型

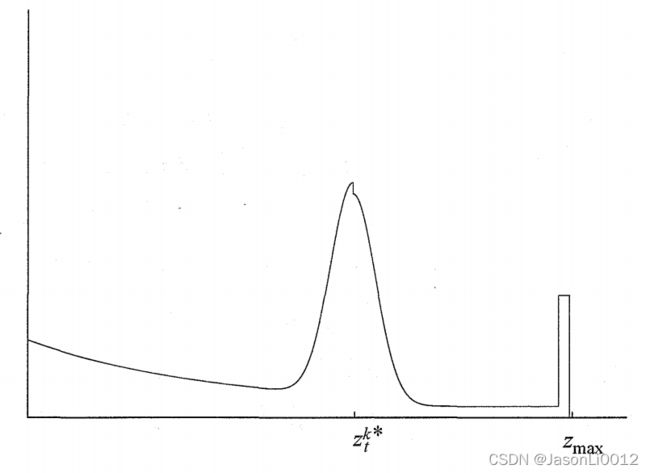
将上述四类噪声模型通过参数$z_{hit}、z_{short}、z_{max}、z_{rand}$进行加权平均混合，得到波束模型$p(z_t^k|x_t,m)$
$$p(z_t^k|x_t,m)={\left[\begin{array}{c}{z}_{hit}\\ z_{short}\\ z_{max}\\ z_{rand}\end{array}\right]}^T\cdot \left[\begin{array}{c}{p}_{hit}(z_t^k|x_t,m)\\ p_{short}(z_t^k|x_t,m)\\ p_{max}(z_t^k|x_t,m)\\ p_{rand}(z_t^k|x_t,m)\end{array}\right]$$
参数间满足和为1的条件：
$$z_{hit}+z_{short}+z_{max}+z_{rand}=1$$
所得模型如图所示：

模型算法

针对测量模型，可设计如下算法实现该模型：

系统输入： 完整的一组测量数据$z_t$、机器人位姿$x_t$、地图环境信息$m$

系统输出： 期望概率$p(z_t^k|x_t,m)$
$$\begin{array}{rl}& Algorithmbeam\_range\_finder\_model(z_t,x_t,m):\\ 1:& q=1\\ 2:& fork=1tokdo\\ 3:& compute{z}_t^{k\ast }forthemeasurement{z}_t^{k}usingraycasting\\ 4:& p=z_{hit}\cdot p_{hit}(z_t^k|x_t,m)+z_{short}\cdot p_{short}(z_t^k|x_t,m)+z_{max}\cdot p_{max}(z_t^k|x_t,m)+z_{rand}\cdot p_{rand}(z_t^k|x_t,m)\\ 5:& q=q\cdot p\\ 6:& returnq\end{array}$$
其中，首先定义变量$q$用于存储概率密度（第一行）。

随后，遍历所有测量数据（第二行），对其内每个数据$z_t^k$采用射线投影法计算其实际距离$z_t^{k\ast }$（第三行）

再次，对每个实际距离$z_t^{k\ast }$采用波束模型计算其期望概率（第四行），并将其累乘至$q$中（第五行）

最终，完整遍历完所有数据后，得到测距仪得到的这一组距离值$z_t$的概率并返回（第六行）。

模型内参

传感器模型参数$\Theta$包括了混合参数$z_{hit}、z_{short}、z_{max}、z_{rand}$以及参数${\sigma }_{hit}$和参数${\lambda }_{short}$。任何传感器测量的似然就是$\Theta$的函数。

通常，可以通过实际数据得到模型的内参。假设参考数据集为$Z=\{z_i\}$、机器人位姿$X=\{x_i\}$、地图信息$m$，其中$z_i$表示每个实际的测量数据；$x_i$表示测量被采纳时机器人的位姿，则可对数据集$Z$进行极大似然估计，从而得到模型的内参：
$$p(Z|X,m,\Theta )$$
为推导极大似然估计，定义一致性变量$c_i$用于表示一个测量值$z_i$产生的可能途径。

波束模型具有四类噪声途径参数测量值$z_i$，则$c_i$的取值有四种类型：$hit$、$short$、$max$、$rand$

对于模型的极大似然估计，首先假设已知一致性变量$c_i$情况下的求解，并由此推广至其未知情况下的求解。

假设已知$c_i$取值

此时，可将测试集$Z$划分为四类不相交的数集，$Z_{hit}$、$Z_{short}$、$Z_{max}$、$Z_{rand}$：
$$\begin{gathered} Z_{hit}\bigcup Z_{short}\bigcup Z_{max}\bigcup Z_{rand}=Z \\ {Z}_{hit}\bigcap Z_{short}=Z_{hit}\bigcap Z_{max}=Z_{hit}\bigcap Z_{rand}=\varnothing \\ {Z}_{short}\bigcap Z_{max}=Z_{short}\bigcap Z_{rand}=Z_{max}\bigcap Z_{rand}=\varnothing \end{gathered}$$

混合参数的极大似然估计

对数据集进行归一化，可得混合参数的极大似然估计：
$$\left[\begin{array}{c}{z}_{hit}\\ z_{short}\\ z_{max}\\ z_{rand}\end{array}\right]=|Z{|}^{-1}\left[\begin{array}{c}|Z_{hit}|\\ |Z_{short}|\\ |Z_{max}|\\ |Z_{rand}|\end{array}\right]$$

固有参数${\sigma }_{hit}$的极大似然估计

首先，求解似然函数：
$$\begin{array}{rl}p(Z_{hit}|X,m,\Theta )=& \prod _{z_i\in Z_{hit}}{p}_{hit}(z_i|x_i,m,\Theta )\\ =& \prod _{z_i\in Z_{hit}}\frac{1}{\sqrt{2\pi {\sigma }_{hit}^2}}exp(-\frac{1}{2}\frac{(z_i-z_i^{\ast }{)}^2}{{\sigma }_{hit}^2})\end{array}$$
式中，$z_i^{\ast }$表示由机器人位姿$x_i$及地图信息$m$计算得到的实际距离。

其次，求解对数似然函数表达式（两边取自然对数）：
$$\begin{array}{rl}\ln p(Z_{hit}|X,m,\Theta )=& \sum _{z_i\in Z_{hit}}[-\frac{1}{2}\ln (2\pi {\sigma }_{hit}^2)-\frac{1}{2}\frac{(z_i-z_i^{\ast }{)}^2}{{\sigma }_{hit}^2}]\\ =& -\frac{1}{2}\sum _{z\in Z_{hit}}[\ln (2\pi {\sigma }_{hit}^2)+\frac{(z_i-z_i^{\ast }{)}^2}{{\sigma }_{hit}^2}]\\ =& -\frac{1}{2}\sum _{z\in Z_{hit}}[\ln (2\pi )+2\ln ({\sigma }_{hit})+\frac{(z_i-z_i^{\ast }{)}^2}{{\sigma }_{hit}^2}]\\ =& -\frac{1}{2}[|Z_{hit}|\cdot \ln (2\pi )+|Z_{hit}|\cdot 2\ln ({\sigma }_{hit})+\sum _{z\in Z_{hit}}\frac{(z_i-z_i^{\ast }{)}^2}{{\sigma }_{hit}^2}]\\ =& -\frac{|Z_{hit}|}{2}\cdot \ln (2\pi )-|Z_{hit}|\cdot \ln ({\sigma }_{hit})-\frac{1}{2{\sigma }_{hit}^2}\sum _{z\in Z_{hit}}(z_i-z_i^{\ast }{)}^2\end{array}$$
将对数似然函数对参数${\sigma }_{hit}$求偏导并使其为0：
$$\begin{array}{rl}\frac{\partial \ln p(Z_{hit}|X,m,\Theta )}{\partial {\sigma }_{hit}}& =0\\ -\frac{|Z_{hit}|}{{\sigma }_{hit}}+\frac{1}{{\sigma }_{hit}^3}\sum _{z_i\in Z_{hit}}(z_i-z_i^{i\ast }{)}^2& =0\\ \frac{1}{{\sigma }_{hit}^3}\sum _{z_i\in Z_{hit}}(z_i-z_i^{i\ast }{)}^2& =\frac{|Z_{hit}|}{{\sigma }_{hit}}\\ \sum _{z_i\in Z_{hit}}(z_i-z_i^{i\ast }{)}^2& =|Z_{hit}|{\sigma }_{hit}^2\end{array}$$
由此，得到似然对数的极大值，也即参数${\sigma }_{hit}$的极大似然估计：
$${\sigma }_{hit}=\sqrt{\frac{1}{|Z_{hit}|}\cdot \sum _{z_i\in Z_{hit}}(z_i-z_i^{i\ast }{)}^2}$$

固有参数${\lambda }_{short}$的极大似然估计

同样，先计算固有参数${\lambda }_{short}$的似然函数：
$$\begin{array}{rl}p(Z_{short}|X,m,\Theta )=& \prod _{z_i\in Z_{short}}{p}_{short}(z_i|x_i,m,\Theta )\\ =& \prod _{z_i\in Z_{short}}[{\lambda }_{short}\cdot exp(-{\lambda }_{short}{z}_i)]\end{array}$$
两侧求自然对数，得到似然函数对数形式：
$$\begin{array}{rl}\ln p(Z_{short}|X,m,\Theta )=& \sum _{z_i\in Z_{short}}[\ln {\lambda }_{short}-{\lambda }_{short}\cdot z_i]\\ =& |Z_{short}|\cdot \ln {\lambda }_{short}-{\lambda }_{short}\sum _{z_i\in Z_{short}}{z}_i\end{array}$$
对其两侧求对参数${\lambda }_{short}$的偏导，并使其为零：
$$\begin{array}{rl}\frac{\partial \ln p(Z_{short}|X,m,\Theta )}{\partial {\lambda }_{short}}& =0\\ \frac{|Z_{short}|}{{\lambda }_{short}}-\sum _{z_i\in Z_{short}}{z}_i& =0\\ \frac{|Z_{short}|}{{\lambda }_{short}}& =\sum _{z_i\in Z_{short}}{z}_i\end{array}$$
由此，得到似然对数的极大值，也即参数${\lambda }_{short}$的极大似然估计：
$${\lambda }_{short}=\frac{|Z_{short}|}{{\sum }_{z_i\in Z_{short}}{z}_i}$$

未知$c_i$取值

上述推导假设参数$c_i$已知，将其推广至参数$c_i$未知情况下。设计采用期望值最大算法（Expectation Maximization，EM）实现两步迭代：

• 计算$c_i$的期望值
• 在该期望下计算模型参数

期望计算

首先，定义数据集$Z$的似然函数：
$$\begin{array}{rl}p(Z|X,m,\Theta )=& \prod _{z_i\in Z}p(z_i|x_i,m,\Theta )\\ =& \prod _{z_i\in Z_{hit}}{p}_{hit}(z_i|x_i,m)\cdot \prod _{z_i\in Z_{short}}{p}_{short}(z_i|x_i,m)\cdot \\ & \prod _{z_i\in Z_{max}}{p}_{max}(z_i|x_i,m)\cdot \prod _{z_i\in Z_{rand}}{p}_{rand}(z_i|x_i,m)\end{array}$$
对似然函数两侧进行自然对数：
$$\begin{array}{rl}\ln p(Z|X,m,\Theta )=& \sum _{z_i\in Z_{hit}}\ln p_{hit}(z_i|x_i,m)+\sum _{z_i\in Z_{short}}\ln p_{short}(z_i|x_i,m)+\\ & \sum _{z_i\in Z_{max}}\ln p_{max}(z_i|x_i,m)+\sum _{z_i\in Z_{rand}}\ln p_{rand}(z_i|x_i,m)\end{array}$$
将变量$c_i$带入上式，可知数据集$Z$内测量值$z_i$将采用对应的噪声模型计算：
$$\begin{array}{rl}\ln p(Z|X,m,\Theta )=\sum _{z_i\in Z}[& I(c_i=hit)\cdot \ln p_{hit}(z_i|x_i,m)\\ +& I(c_i=short)\cdot \ln p_{short}(z_i|x_i,m)\\ +& I(c_i=max)\cdot \ln p_{max}(z_i|x_i,m)\\ +& I(c_i=rand)\cdot \ln p_{rand}(z_i|x_i,m)]\end{array}$$
由于参数$c_i$未知，则次啊用期望最大算法，希望对上式计算最大期望：
$$\begin{array}{rl}1:E[\ln p(Z|X,m,\Theta )]=\sum _i[& p(c_i=hit)\cdot \ln p_{hit}(z_i|x_i,m)+p(c_i=short)\cdot \ln p_{short}(z_i|x_i,m)+\\ & p(c_i=max)\cdot \ln p_{max}(z_i|x_i,m)+p(c_i=rand)\cdot \ln p_{rand}(z_i|x_i,m)]\\ 2：E[\ln p(Z|X,m,\Theta )]=:\sum _i[& e_{i,hit}\cdot \ln p_{hit}(z_i|x_i,m)+e_{i,short}\cdot \ln p_{short}(z_i|x_i,m)+\\ & e_{i,max}\cdot \ln p_{max}(z_i|x_i,m)+e_{i,rand}\cdot \ln p_{rand}(z_i|x_i,m)]\end{array}$$
式中，第二行符号$=:$含义为记作 ，其中参数$e_{i,hit}、e_{i,short}、e_{i,max}、e_{i,rand}$表示有这四种模型引起的产生测量值$z_i$的概率：
$$\left[\begin{array}{c}{e}_{i,hit}\\ e_{i,short}\\ e_{i,max}\\ e_{i,rand}\end{array}\right]:=\left[\begin{array}{c}p(c_i=hit)\\ p(c_i=short)\\ p(c_i=max)\\ p(c_i=rand)\end{array}\right]=\eta \left[\begin{array}{c}{p}_{hit}(z_i|x_i,m)\\ p_{short}(z_i|x_i,m)\\ p_{max}(z_i|x_i,m)\\ p_{rand}(z_i|x_i,m)\end{array}\right]$$
式中，符号$:=$表示意为。$\eta$为归一化因子：
$$\eta =[p_{hit}(z_i|x_i,m)+p_{short}(z_i|x_i,m)+p_{max}(z_i|x_i,m)+p_{rand}(z_i|x_i,m){]}^{-1}$$

极大似然估计

极大似然估计的混合参数为归一化的期望：
$$\left[\begin{array}{c}{z}_{hit}\\ z_{short}\\ z_{max}\\ z_{rand}\end{array}\right]=|Z{|}^{-1}\sum _i\left[\begin{array}{c}{e}_{i,hit}\\ e_{i,short}\\ e_{i,max}\\ e_{i,rand}\end{array}\right]$$
极大似然估计的参数${\sigma }_{hit}$及${\lambda }_{short}$可将上述在已知$c_i$取值情况下，计算所得的表达式中的硬分配替换为用期望加权的软分配，从而推广至未知$c_i$取值下的表达式：
$${\sigma }_{hit}=\sqrt{\frac{1}{{\sum }_{z_i\in Z}{e}_{i,hit}}\cdot \sum _{z_i\in Z}{e}_{i,hit}(z_i-z_i^{i\ast }{)}^2}$$

$${\lambda }_{short}=\frac{{\sum }_{z_i\in Z}{e}_{i,short}}{{\sum }_{z_i\in Z}{e}_{i,short}{z}_i}$$

参数调节算法

系统输入： 测距仪测量数据集$Z$、机器人位姿数据集$X$、地图信息$m$

系统输出： 模型内参$\Theta$
$$\begin{array}{rl}& Algorithmlearn\_intrinsic\_parameters(Z,X,m):\\ 1:& repeatuntilconvergencecritensatisfied\\ 2:& forall{z}_{i}inZdo\\ 3:& \eta =[p_{hit}(z_i|x_i,m)+p_{short}(z_i|x_i,m)+p_{max}(z_i|x_i,m)+p_{rand}(z_i|x_i,m){]}^{-1}\\ 4:& calculate{z}_i^{\ast }\\ 5:& e_{i,hit}=\eta p_{hit}(z_i|x_i,m)\\ 6:& e_{i,short}=\eta p_{short}(z_i|x_i,m)\\ 7:& e_{i,max}=\eta p_{max}(z_i|x_i,m)\\ 8:& e_{i,rand}=\eta p_{rand}(z_i|x_i,m)\\ & \\ 9:& z_{hit}=|Z{|}^{-1}\sum _i{e}_{i,hit}\\ 10:& z_{short}=|Z{|}^{-1}\sum _i{e}_{i,short}\\ 11:& z_{max}=|Z{|}^{-1}\sum _i{e}_{i,max}\\ 12:& z_{rand}=|Z{|}^{-1}\sum _i{e}_{i,rand}\\ 13:& {\sigma }_{hit}=\sqrt{\frac{1}{{\sum }_i{e}_{i,hit}}\cdot \sum _i{e}_{i,hit}(z_i-z_i^{i\ast }{)}^2}\\ 14:& {\lambda }_{short}=\frac{{\sum }_i{e}_{i,short}}{{\sum }_i{e}_{i,short}{z}_i}\\ 15:& return\Theta =\{z_{hit},z_{short},z_{max},z_{rand},{\sigma }_{hit},{\lambda }_{short}\}\end{array}$$
第三行，计算归一化因子

第四行，有机器人位姿及地图信息，计算测量值的实际值，也即在地图环境$m$下机器人处于位姿$x_i$时提取到的测距值$z_i^{\ast }$

第五行~第八行，计算由四类噪声模型独立引起产生测量值$z_i$的概率

第九行~第十四行，遍历完成后计算模型的六个内参

算法采用期望最大化算法实现极大似然估计参数，通过迭代数据实现对内参的迭代优化。

算法效果

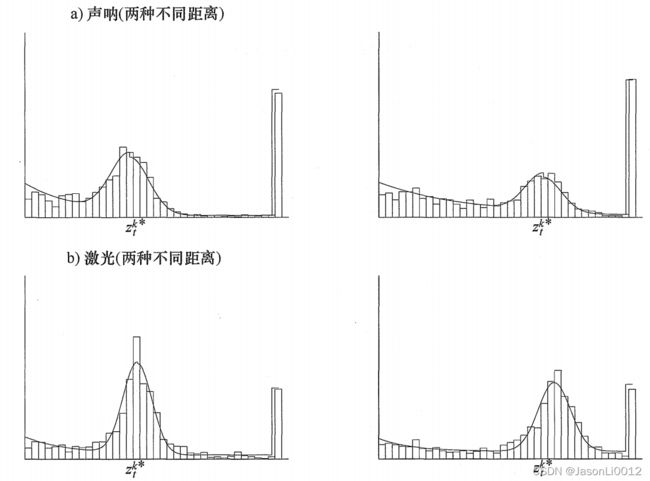
如图为两组机器人在办公室环境下获取到的10 000个测量数据，左图为声纳传感器测量数据，右图为激光传感器测量数据。图中x轴为计数个数，y轴为传感器测量距离：

其中，测量的期望范围为3m，也即真实距离300cm，最大量程为500cm。用所设计的极大似然估计参数模型测试，得到如下效果图。

其中，左侧数据为采用上述测试集测试得到的图像（$z_t^{k\ast }=3$）；右侧一组则为对照数据的分布图像（$z_t^{k\ast }>3$），由图可以分析得到：

• 实际距离$z_t^{k\ast }$越小，模型测量的数据越精准
• 短距离测量的高斯分布（左侧）较长距离测量的高斯分布（右侧）更窄
• 激光传感器（b组）比超声波传感器（a组）测量更准确，（高斯分布更窄且最大值分布更少）

同时给出一组$180°$激光传感器的扫描环境图，该机器人被已经获得地图信息$m$的占用栅格地图中走廊位置处，扫描自身周围的环境：

则下图中，给出了地图信息与测量似然$p(z_t|x_t,m)$映射到$x-y$空间的平面图，其中显示颜色越深处，机器人处于该位置的可能性就越高。

上图显示，所有高似然区域处于走廊中，这和机器人的实际情况相符合。同时概率分散在整个走廊上也表明单一传感器难以确切确定机器人位姿。（走廊环境大致相同，无特殊特征，难区分）

同时，后验有规则地分布在两条水平带状区上是因为难以确定机器人的航向，由此形成两种可能的朝向对应两条区域。

局限性

波束模型需要耗费大量计算力，用于对每一个单一测量$z_t^k$通过射线投影计算其实际测量$z_t^{k\ast }$。如激光雷达每次扫描将得到一组$180°$的数据，对这180个数据需要逐一进行计算，将耗费大量时间与计算量。

此外，该模型缺乏光滑性。在由许多小障碍的混乱环境中，概率分布$p(z_t^k|x_t,m)$在机器人位姿$x_t$处很不光滑。机器人位姿的小变化将引起测距模型大的位移变化。