贪心算法（小记）

区间贪心

试一下做法，区间问题无外乎就是排序，要么按左端点排序，要么按右端点排序，要么双关键字排序
所以贪心的题如果没有什么思路的话，可以自己试一下
试完之后举一些例子看看自己的做法是不是对的，如果没问题的话，可以尝试证明一下这个算法

贪心算法一般就是猜+证明
贪心题有个特点就是每次都选择当前最好的情况走过去

先来个例题吧

我的思路就是找一下交集，有交集取交集，没交集取全集

然后发现还可以简化，你排序之后，直接找最边上的点，看看这个点在那几个集合，在的集合就直接删去

这个怎么证明对呢？假设答案是res，然后选出来的点是ans个 ，证明res<=ans, res>=ans就行
证明第一个：你要每个区间都有点，res里面你已经去掉了有重合的部分公共的点，这个很好理解吧
第二个：由题意可得，我选择的区间有一个关系就是，两两之间没有任何一个相交，然后你想要覆盖ans个区间，你最少就是要用ans个，也就是res>=ans

#include 
#include 

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &W)const
    {
        return r < W.r;
    }
}range[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n);

    int res = 0, ed = -2e9;//res是选了多少个点，ed是选的上一个点的下标 
    for (int i = 0; i < n; i ++ )
        if (range[i].l > ed)
        {
            res ++ ;
            ed = range[i].r;
        }

    printf("%d\n", res);

    return 0;
}

好问题啊这问题竟然跟上面那个一样，不说了，代码也一样。
不过有意思的是，这里是最大值，证明不太一样，还是设res是答案，ans是选择的方案数，由于res是所有的互不相交的区间的最大值，所以res>=ans
第二个直接证，选完ans个区间，每个区间都至少有一个点了，假设res > ans，如果我们有>ans个不相交的区间的话，ans一定覆盖不完全，所以res<=ans

一般来说就是考个模型，也就是之前出现过的问题，区间贪心问题一般都是排序

再来个区间题目

有多个组符合题意，随便挑一个扔进去就行

证明一下：

ans是答案，cnt是按照算法得到的组数
cnt按照上述算法一定是一个合法方案，然后ans是最小的，所以ans一定小于等于cnt
当开第cnt个组的时候，我们发现，前cnt-1个组一定是跟第cnt个组有公共点的，也就是都至少能在每一个组里面找出来一个点，有公共点，我们就可以 直接当成cnt那个区间的左端点，然后那个点就是所有的公共点，然后就发现至少要分cnt组，所以cnt<=ans.
综上 ans就是答案

#include 
#include 
#include 

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &W)const
    {
        return l < W.l;
    }
}range[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }

    sort(range, range + n);

    priority_queue<int, vector<int>, greater<int>> heap;//存的是所以的组的最大的r 
    for (int i = 0; i < n; i ++ )
    {
        auto r = range[i];
        if (heap.empty() || heap.top() >= r.l) heap.push(r.r);
        else
        {
            heap.pop();
            heap.push(r.r);
        }
    }

    printf("%d\n", heap.size());

    return 0;
}

区间覆盖

正确性：

首先，按照上诉算法能够找出来的一定是一个可行方案，把这个方案中区间的数量记成cnt，ans表示所有可行方案里面的最小值，所以ans<=cnt;
第二个:对于每一个ans都可以由任意的cnt挨个替换区间，每次替换都不会增加区间的数量，然后替换成cnt，然后就会发现其实ans就是等于cnt

所以这个题是可以直接证明相等的，任何一个ans都可以挨个区间替换，然后变成cnt

设起点为start，终点为end，其中start每一次被覆盖后，都变成新加区间的最右端

#include 
#include 

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &W)const
    {
        return l < W.l;
    }
}range[N];

int main()
{
    int st, ed;
    scanf("%d%d", &st, &ed);
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }

    sort(range, range + n);

    int res = 0;
    bool success = false;
    for (int i = 0; i < n; i ++ )
    {
        int j = i, r = -2e9;
        while (j < n && range[j].l <= st)//遍历所有在start左边的这些区间的右端点，最大值是多少 
        {
            r = max(r, range[j].r);
            j ++ ;
        }

        if (r < st)
        {
            res = -1;
            break;
        }

        res ++ ;
        if (r >= ed)
        {
            success = true;
            break;
        }

        st = r;
        i = j - 1;
    }

    if (!success) res = -1;
    printf("%d\n", res);

    return 0;
}

哈夫曼树

例题

很简单，每次挑两个最小的合并就行

证明：
第一个要证明的是，数最小的两个数，一定是这个树深度最深的两个节点，并且可以是兄弟节点，也就是我们第一步就把他们合并
合并一次之后的n-1个果子的最优解，一定是n个果子的最优解吗
证明：f(n) = f(n-1)+a+b,也就是合并n个果子可以由合并n-1个果子加上a+b得到，
也就是f(n) = f(n-1)+a+b，由于第一步都是将a和b合并，也就是a+b，然后a+b就可以都先去掉，然后再求最小值，也就是求f(n-1)的最小值

#include 
#include 
#include 

using namespace std;

int main()
{
    int n;
    scanf("%d", &n);

    priority_queue<int, vector<int>, greater<int>> heap;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        heap.push(x);
    }

    int res = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        res += a + b;
        heap.push(a + b);
    }

    printf("%d\n", res);
    return 0;
}

排序不等式

例题

这个题比较简单，直接从小到大排序就行

证明：如果不是按照从小到大拍，就一定存在两个连续的，前边比后边大
这时候把两个人交换位置，对其他人没有影响，发现交换前比交换后大，然后就证明完了
一般来说，贪心问题的证明，最常用的还是反证法
还有一个证明两个方向，一个大于等于，一个小于等于
数学归纳法也是可以的

绝对值不等式

例题来咯
排序不等式
我们可以把这些点的值设出来，然后看一下公式长什么样子，然后从公式的角度推一下我们的最小值应该是什么样子

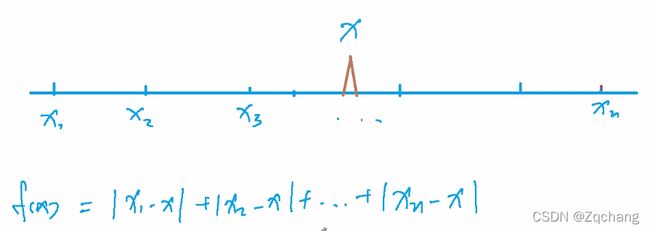
把这个公式分成若干组，第一个和最后一个一组，第二个和倒数第二个一组…

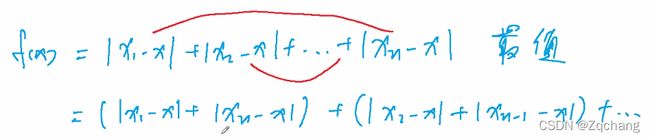
问题也就转化为

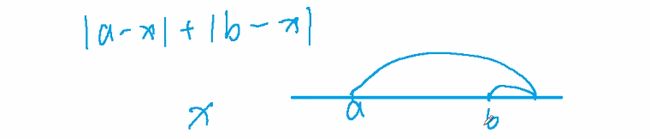
也就是只要x在他们之间就行，上述公式也就

如果n是偶数等号在中心两个点之间（包含那两个点）能实现， 如果是奇数就是中间那个数也就直接a[n/2]

#include 
#include 

using namespace std;

const int N = 100010;

int n;
int q[N];

int main()
{
    scanf("%d", &n);

    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    sort(q, q + n);

    int res = 0;
    for (int i = 0; i < n; i ++ ) res += abs(q[i] - q[n / 2]);

    printf("%d\n", res);

    return 0;
}

推公式

例题

贪心问题里面，很多都是先把公式推出来，然后从公式的角度，用一些不等式的原理，如均值不等式，柯西不等式，绝对值不等式，贪心中涉及到的模型大多为在数学里面被研究过的
结论：

证明，

这样的排法一定是大于等于最优解，因为最优解一定是方案中最小的那一个
第二个：假设最优解不是按照上述方法排序，那么它一定存在相邻的两头牛
wi + si >w(i+1) + s(i+1)
假如交换一下他俩

消去同类项

同时加上si + s(i+1)

然后根据数据范围，可以得到，si < wi + si，并且已知的是wi +si > w(i+1) + s(i+1)
所以交换后的那一行，两个数里面的最大值一定小于交换前两个里面的最大值，也就是最大值一定变小了
所以只要存在逆序，我们把它正过来之后，最起码能够保证，最大值不会变大，
也就是我们的最优解如果不是从小到大递增的，那我们一定可以把他们变成从小到大递增的，而且变的过程中，最大值一定是不会变大的，也就是得到的解小于等于最优解，因此第二问部分得证、

#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 50010;

int n;
PII cow[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int s, w;
        scanf("%d%d", &w, &s);
        cow[i] = {w + s, w};
    }

    sort(cow, cow + n);

    int res = -2e9, sum = 0;
    for (int i = 0; i < n; i ++ )
    {
        int s = cow[i].first - cow[i].second, w = cow[i].second;
        res = max(res, sum - s);
        sum += w;
    }

    printf("%d\n", res);

    return 0;
}