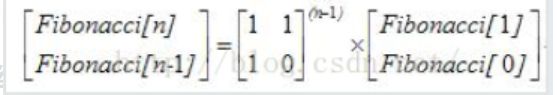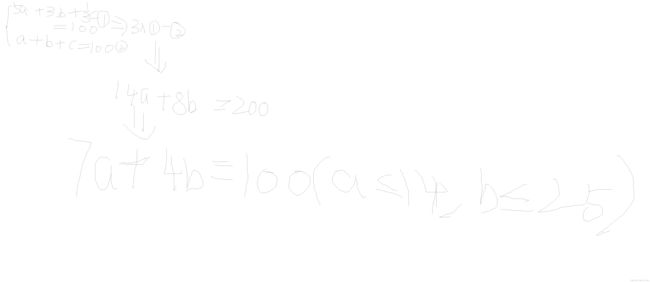C语言课程设计——25道蓝桥杯练习题
文章目录
- 一、基础练习
-
- 1.fib数列
-
- 题目
- 解题思路
- 解题代码
-
- 解法一(简单递推):时间复杂度O(n)
- 解法二(矩阵快速幂):时间复杂度O(logn)
- 2.闰年判断
-
- 题目
- 解题思路
- 解题代码
- 3. 数列特征
-
- 题目
- 解题思路
- 解题代码
- 4.查找整数
-
- 题目
- 解题思路
- 解题代码
-
- 解法一:C风格
- 解法二:C++风格
- 5.杨辉三角形
-
- 题目
- 解题思路
- 解题代码
- 6.数列排序
-
- 题目
- 解题思路
- 解题代码
- 7.算法训练 P0701 单词变复数
-
- 题目
- 题目详解
- 解题代码
- 8.算法训练 P0702 实现strcmp
-
- 题目
- 解题思路
- 解题代码
- 9.试题 算法训练 P0703 反置数
-
- 题目
- 解题思路
- 解题代码
- 10.试题 算法训练 P0704 满足条件的回文数和质数
-
- 题目
- 解题思路
- 解题代码
- 11.试题 算法训练 P0601 实现删除字符函数
-
- 题目
- 解题思路
- 解题代码
-
- 解法一:只为解题的解题(适合真正比赛时)
- 解法二:从左到右的扫描更新法 O(n) (使用于面试官问你后,你的回答)
- 12.试题 算法训练 P1103 复数加减乘除类的设计
-
- 题目
- 解题思路
- 解题代码
- 13.试题 算法训练 删除数组零元素
-
- 题目
- 解题思路
- 解题代码
- 14.试题 算法训练 大整数加法
-
- 题目
- 解题思路
- 解题代码
- 15.试题 算法训练 最小乘积(基本型)
-
- 题目
- 解题思路
- 解题代码
- 16.试题 算法训练 矩阵运算
-
- 题目
- 解题思路
- 解题代码
- 17.试题 算法训练 百鸡百钱
-
- 题目
- 解题分析
- 解题代码
- 18.试题 算法训练 数据传递加密
-
- 题目
- 题目解析
- 解题代码
- 二、算法提高
-
- 19. 试题 算法提高 心形
-
- 题目
- 题目解析
- 解题代码
- 20.试题 算法提高 字符串查找
-
- 题目
- 题目解析
- 解题代码
- 21.试题 算法提高 校门外的树
-
- 题目
- 解题思路
- 解题代码
- 22.试题 算法提高 第二大整数
-
- 题目
- 解题分析
- 解题代码
- 三、历届试题
-
- 23.四平方和【第七届】【省赛】【C组】
-
- 题目
- 题目解析
- 解题代码
- 24.历届真题 错误票据【第四届】【省赛】【B组】
-
- 题目
- 题目解析
- 解题代码
- 25. 历届真题 密码发生器【第三届】【省赛】【本科组】
-
- 题目
- 题目解析
- 解题代码
一、基础练习
1.fib数列
题目
题目链接
Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。
数据规模与约定
1 <= n <= 1,000,000。
解题思路
很明显,数据规模并不大,O(n)时间复杂度便可解决。
但如果数据规模非常庞大,我们可以利用到下面这张图的矩阵递推公式再根据矩阵快速幂解决:
解题代码
解法一(简单递推):时间复杂度O(n)
适用于数据量少于10^8的情况
#include 解法二(矩阵快速幂):时间复杂度O(logn)
适用于数据量大于10^8的情况
//
// Created by Alone on 2021/11/19.
//
#include 2.闰年判断
题目
题目链接
解题思路
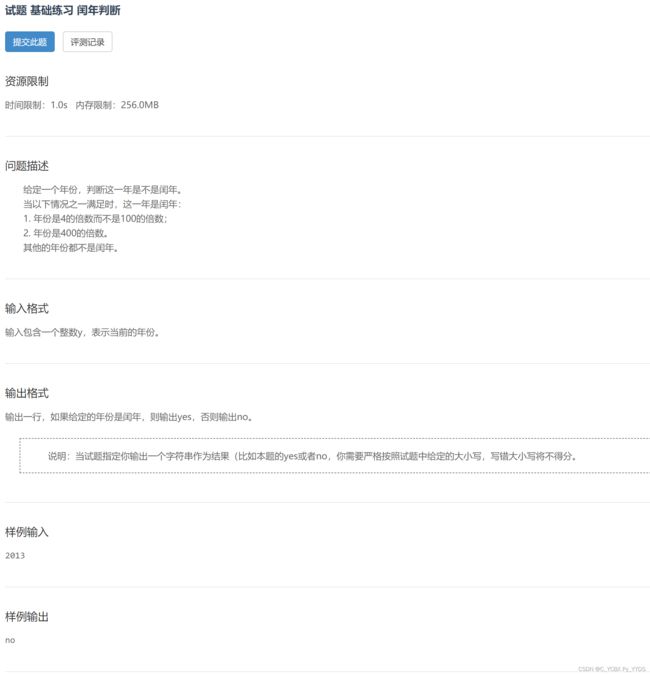
只要挑选处闰年即可,闰年有个判断方式将其判断:
关于闰年的解释:
- 普通年份能被4整除,且不能被100整除的,是闰年。( 如2004年就是闰年)
- 世纪年份能被400整除的是闰年。( 如2000年是闰年,1900年不是闰年)
如果年份是闰年,那么它的二月份就会比平常多1天。
解题代码
#include3. 数列特征
题目
题目链接
解题思路
求一个数组的最大值和最小值以及所有数字的和。。
解题代码
#include4.查找整数
题目
题目链接
解题思路
按照题目意思来就行,直接查找第一次出现的位置即可。
解题代码
解法一:C风格
#include 解法二:C++风格
由于C++98不支持lamda表达式,所以需要把传入的函数单独写出来了。
#include C++11风格
#include 5.杨辉三角形
题目
题目链接
解题思路
根据杨辉三角的性质来做,对于杨辉三角第 i 行、第 j 列的元素,我们用 dp[i][j] 来进行表示,那么有以下关系:
d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − 1 ] ( 0 < j < m ) 1 ( j = 0 , j = m ) dp[i][j] = \left\{ \begin{array}{l} dp[i-1][j]+dp[i-1][j-1](0
解题代码
#include 6.数列排序
题目
题目链接
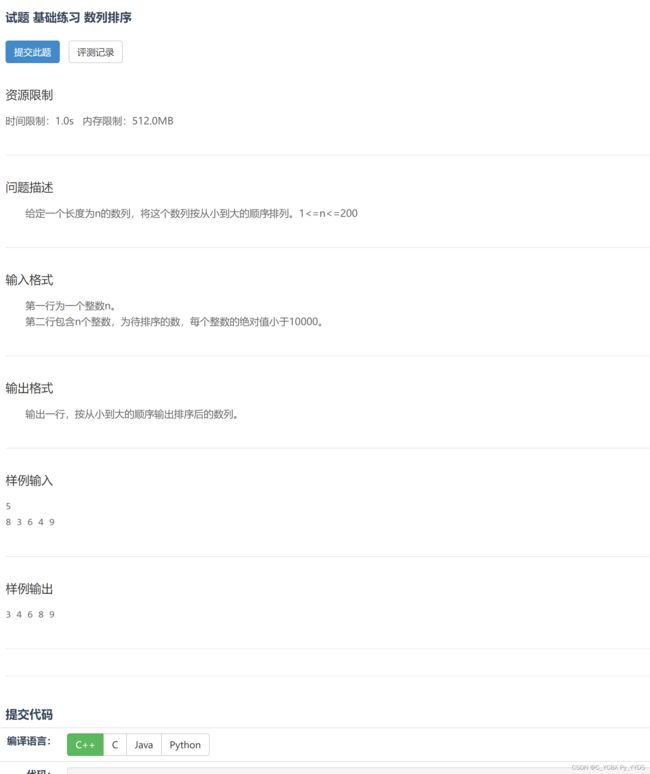
解题思路
排序算法,有很多,有冒泡/插入/选择/基数/基尔/快速/堆/归并/桶排序等等等,这些大概是10大必会的排序,其中以快排运用最广,而快排,又分几种实现方式,大概分两类,基于比较的挖坑填补实现,以及直接基于比较的交换实现。我这里手写的快排用的是交换实现。
解题代码
#include 7.算法训练 P0701 单词变复数
题目
题目链接
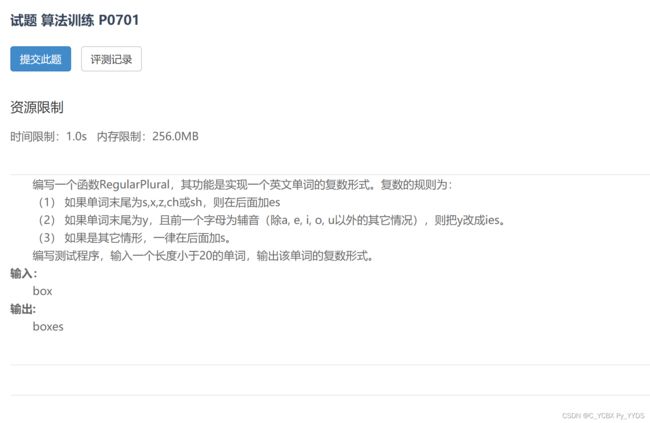
题目详解
简单明了的三种分类讨论,我这里实现一个专门判断是否以某个字符结尾的函数,然后一切就引刃而解了。
解题代码
完全的纯种C优质代码:
#include 8.算法训练 P0702 实现strcmp
题目
题目链接
解题思路
- 由于我平时是比较对源码感兴趣的,所以本人也比较喜欢写这种造轮子的题目。
strcmp的比较无非就是三种情况:
- 完全匹配,如"abc",“abc”
- 部分匹配,如"abcd",“abf”
- 单方面完全匹配,如"abcd",“ab”
而计算差值的时候我们就需要对以上三种情况进行思考。
接下来结合代码应该就非常好理解了。
解题代码
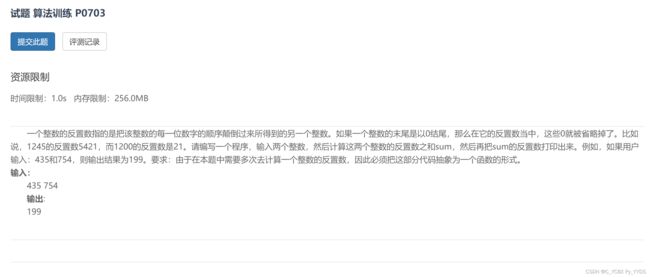
#include 9.试题 算法训练 P0703 反置数
题目
题目链接
解题思路
我认为有至少两种解题思路:
- 按照题目给的过程进行模拟,这个过程其实也很简单,直接就写两个函数就可以解决问题:
一个用于去掉后缀0的函数以及一个用于把整数的数值反转的函数。这个方法非常好写,也很快,但如果数字很大就没法了。 - 通过字符串模拟加法过程,恰好字符串大数加减的正常过程就是先反转再加减的,而这题正好就是需要反向加减。所以完全可以用字符串模拟大数加减解决。但我们需要对字符串前后的0进行处理,否则不符合打印要求。(正好后面还有大数加减的题目,我就偷个懒用它了)
解题代码
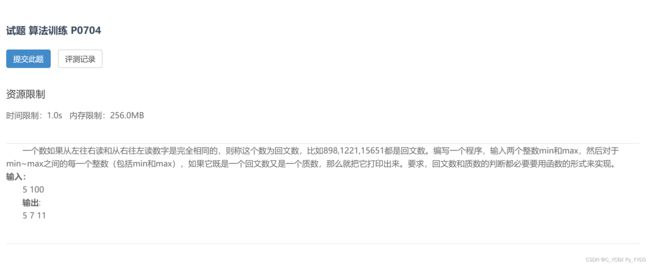
#include 10.试题 算法训练 P0704 满足条件的回文数和质数
题目
题目链接
解题思路
分离连个逻辑函数即可简单实现功能:
- 判断是否为质数。
- 判断是否是回文数。
这两个数的判断都有多种方法进行,这里不过多赘述。
我用的都是最质朴的方法进行判断。
解题代码
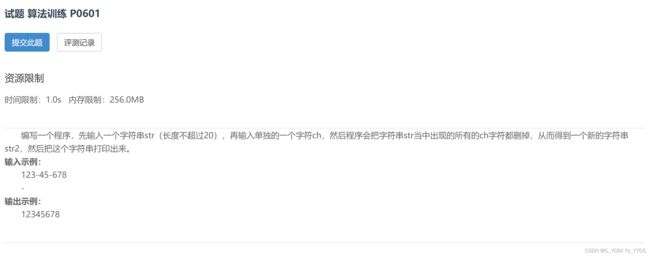
#include 11.试题 算法训练 P0601 实现删除字符函数
题目
题目链接
解题思路
如果这题只是为了解题,那么很简单,直接碰到这个字符就不打印即可。
如果是为了实现这个删除给定字符的函数功能,我有两种思路:
- 如果不创建新的内存进行删除,那么最直观的方法就是一个一个字符的来进行删除操作,如果等于这个字符,那么直接进行一轮删除后的平移。时间复杂度较高,最坏为O(n^2)。当然可以优化为O(n)级别的,那就是我们采取给整个数组赋值的思路,从左到右扫描赋值,如果等于对应字符,那么就跳过不赋值,最后在后面加个 ‘\0’ 即可。
- 如果创建新内存进行,那么很简单的就可以实现O(n)级别的。
解题代码
解法一:只为解题的解题(适合真正比赛时)
#include 解法二:从左到右的扫描更新法 O(n) (使用于面试官问你后,你的回答)
#include 12.试题 算法训练 P1103 复数加减乘除类的设计
题目
编程实现两个复数的运算。设有两个复数 和 ,则他们的运算公式为:
要求:(1)定义一个结构体类型来描述复数。
(2)复数之间的加法、减法、乘法和除法分别用不用的函数来实现。
(3)必须使用结构体指针的方法把函数的计算结果返回。
说明:用户输入:运算符号(+,-,*,/) a b c d.
输出:a+bi,输出时不管a,b是小于0或等于0都按该格式输出,输出时a,b都保留两位。
输入:
- 2.5 3.6 1.5 4.9
输出: - 1.00±1.30i
解题思路
- 把高中那套负数加减乘除的公式套用进去即可!
这里C的话可用函数式的面向的对象实现,C++的话用一个类重载所有的运算符即可。
解题代码
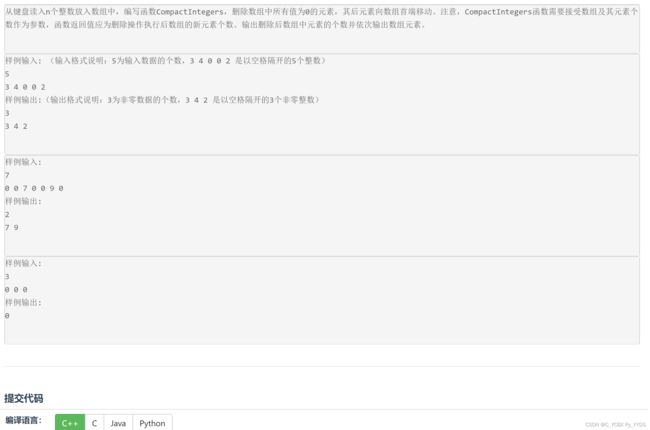
#include 13.试题 算法训练 删除数组零元素
题目
题目链接
解题思路
这和之前的删除字符的题目没有任何的本质区别。就是直接通过一个指针从左到右遍历,而另一个指针从左到右更新。
代码即是思路。
解题代码
#include 14.试题 算法训练 大整数加法
题目
资源限制
时间限制:1.0s 内存限制:256.0MB
问题描述
任意输入两个正整数a,b,求两数之和。(注:本题会输入超过32位整数限制的大整数)
样例输入
4611686018427387903 4611686018427387903
样例输出
9223372036854775806
数据规模和约定
1= 由于前面都用到了大整数加法,所以直接拿前面的代码来用了。具体实现思路也很简单,就是一个加法的模拟过程,一般来说三步走: 资源限制 时间限制:1.0s 内存限制:512.0MB 问题描述 给两组数,各n个。 那么对应乘积取和的最小值应为: 输入格式 第一个行一个数T表示数据组数。后面每组数据,先读入一个n,接下来两行每行n个数,每个数的绝对值小于等于1000。 输出格式 一个数表示答案。 样例输入 样例输出 根据题目意思,很明显,我们把数组的位置,一个排成从小到大,一个排成从大到小,对应相乘即可。 资源限制 时间限制:1.0s 内存限制:512.0MB 问题描述 给定一个n*n的矩阵A,求A+AT的值。其中AT表示A的转置。 输入格式 输入的第一行包含一个整数n。1<=n<=100。 输出格式 输出n行,每行n个整数,用空格分隔,表示所示的答案。 样例输入 3 样例输出 2 6 10 这里直接用二维数组存下矩阵然后得到另一个转置矩阵再相加即可。 我一般碰到这类关于某种数据类型的运算,我喜欢把它们抽象为类,然后再进行计算。所以我这题是设计了一个mat类,里面重载了加法等。 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 我国古代数学家张丘建在《算经》一书中提出的数学问题:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,问鸡翁、鸡母、鸡雏各几何? 输出格式 满足条件的鸡翁、鸡母和鸡雏的只数,中间空格隔开。每种情况输出到一行。 纯纯的用代码解方程,分析草稿如下图: 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 某个公司传递数据,数据是四位整数,在传递过程中需要进行加密的,加密规则如下:每位数字都加上5,然后除以10的余数代替该位数字。再将新生成数据的第一位和第四位交换,第二位和第三位交换。要求输入4位整数,输出加密后的4位整数。比如:输入一个四位整数1234,则输出加密结果为9876。 样例输入 1234 样例输出 9876 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 根据给出的最大宽度,输出心形(注意空格,行末不加多余空格)。 输入格式 一行一个整数width,表示最宽的一行中有多少个“*”。 输出格式 若干行表示对应心形。注意为让选手更清晰观察样例,样例输出中用“-”表示空格,请选手在提交的程序中不要输出“-”。 样例输入 13 样例输出 数据规模和约定 width总是4的倍数加一,且width >= 13。 这种打印类型题目要学会逐一找规律剖析! 在我的写法里面,这个心形能够解分为三个部分:(如下图) 首先我们需要确认一个元素的组成长度!本题输入的就是第二部分的长度,比如样例的13,而我们发现每个部分由两个字符构成,所以我们下面的讨论都是以两个字符为单位。而拆分成不同的元素种类的话也只有两种:1. 以下所有用到的 n 均表示输入的变量值。 一、第一部分 关于第一部分我还是分为三个部分进行每一行的打印: 二、第二部分 第二部分就没有那么多弯弯绕绕了,直接 n 是多少就打印多少个星。 三、第三部分 第三部分分为两部分: 当星元素递减为1个的时候结束! 资源限制 时间限制:1.0s 内存限制:512.0MB 问题描述 给定两个字符串a和b,查找b在a中第一次出现的位置。 输入格式 输入包括两行,分别为两个字符串a和b,字符串中可能含有空格。字符串的长度不超过500。请注意读入一行字符串的方法。 输出格式 输出b在a中第一次出现的位置。如果b没有在a中出现,则输出-1。 样例输入 hello world 样例输出 6 样例输入 hello world 样例输出 -1 题目链接 不知道是不是这道题的缘故,好像只能提交一个函数体内的代码,不能提交完整代码! 所以我都AC代码如下所示: AC截图: 其实本题我是想拿来练练kmp算法的,奈何只能写部分代码块进行提交,连函数都不能写,所以只好作罢。 实际直接调用语言的内部函数库的话,可以像下面这样: C version cpp version 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 某校大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置;数 轴上的每个整数点,即0,1,2,……,L,都种有一棵树。 输入格式 输入文件的第一行有两个整数L(1 <= L <= 10000)和 M(1 <= M <= 100),L代表马路的长度,M代表区域的数目,L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数,用一个空格隔开,表示一个区域的起始点 和终止点的坐标。 输出格式 输出文件包括一行,这一行只包含一个整数,表示马路上剩余的树的数目。 样例输入 500 3 样例输出 298 数据规模和约定 对于20%的数据,区域之间没有重合的部分; 题目链接 这题蓝桥杯平时训练的时候,只能说是写烂了。。这题本可以按照首尾区间 =1 +1 的方式来处理,但是由于本题是删除区间内的元素后不能重复删除的情况,所以目前我只能想到用直接暴力的覆盖法 直接暴力的覆盖: 每次给定区间后,我们就把这个区间的树砍掉,如果树已经被砍(值为0),则没变化。 资源限制 时间限制:1.0s 内存限制:512.0MB 问题描述 编写一个程序,读入一组整数(不超过20个),当用户输入0时,表示输入结束。然后程序将从这组整数中,把第二大的那个整数找出来,并把它打印出来。说明:(1)0表示输入结束,它本身并不计入这组整数中。(2)在这组整数中,既有正数,也可能有负数。(3)这组整数的个数不少于2个。 样例输入 5 8 -12 7 0 样例输出 7 题目链接 如果仅仅只是为了解题,那么这题最简单的方式肯定是直接存下数据排序即可。 当然这道题的正统解法应该是,通过两个变量进行更新即可。 资源限制 时间限制:1.0s 内存限制:256.0MB 四平方和定理,又称为拉格朗日定理: 比如: 对于一个给定的正整数,可能存在多种平方和的表示法。 程序输入为一个正整数N (N<5000000) 例如,输入: 再例如,输入: 再例如,输入: 资源约定: 请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法。 对于以上这句话,你可以理解为,题目要你从四个for循环的正常顺序里面找到第一个符合要求的答案,很多人可能就是没搞清楚这个说明的关键所在。所以直接能用下面这段代码暴力秒了。。。当然也不是直接的一个判断就秒,而需要对每层循环进行判断是否已经超出表示范围,然后排除。 当然这样暴力的方法,当然不是这道题的真正意义,虽然也能够通过 像这种几个for循环找某个数的题目,大概有以下三类优化方法: 很明显我们如果想真正做这类题,正统的方法应该是第三种,我们需要一个哈希表映射值和下标来方便拿取答案。我们可以用STL里面的哈希表用int映射pair是可以的,但效率不够好。由于本题的数据范围其中的值不会太大,所以完全可以用最原始的数组充当哈希表来使用,平时我们在竞赛题中你用哈希表来映射多元的东西,能不用STL就不用,因为查找和遍历的效率太慢了。 两个数组充当哈希表进行提前存储映射,来把4个for优化为2个for。 提交代码的效率: 资源限制 时间限制:1.0s 内存限制:256.0MB 某涉密单位下发了某种票据,并要在年终全部收回。 每张票据有唯一的ID号。全年所有票据的ID号是连续的,但ID的开始数码是随机选定的。 因为工作人员疏忽,在录入ID号的时候发生了一处错误,造成了某个ID断号,另外一个ID重号。 你的任务是通过编程,找出断号的ID和重号的ID。 假设断号不可能发生在最大和最小号。 要求程序首先输入一个整数N(N<100)表示后面数据行数。 要求程序输出1行,含两个整数m n,用空格分隔。 例如: 则程序输出: 再例如: 则程序输出: 资源约定: 请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 注意: main函数需要返回0 提交时,注意选择所期望的编译器类型。 题目链接 读完题后,我们发现,它的输入,我们需要格外注意一下,因为是以行输入,而每行要输入的数据是多少也没告诉你,所以很多人可能会被这个给难到,而实际的解题过程并不复杂,只需要创建一个数组用它的下标将每个你输入的值进行记录,然后如果重复记录则就是第二个输出,在输入的途中,你将他的最小值和最大值给记录下来,最后再遍历一遍数组即可得到中间缺的那个数! 具体数组的细节操作: 具体的输入操作细节: 解题效率: 资源限制 时间限制:1.0s 内存限制:256.0MB 在对银行账户等重要权限设置密码的时候,我们常常遇到这样的烦恼:如果为了好记用生日吧,容易被破解,不安全;如果设置不好记的密码,又担心自己也会忘记;如果写在纸上,担心纸张被别人发现或弄丢了… 这个程序的任务就是把一串拼音字母转换为6位数字(密码)。我们可以使用任何好记的拼音串(比如名字,王喜明,就写:wangximing)作为输入,程序输出6位数字。 变换的过程如下: 第一步. 把字符串6个一组折叠起来,比如wangximing则变为: 第二步. 把所有垂直在同一个位置的字符的ascii码值相加,得出6个数字,如上面的例子,则得出: 第三步. 再把每个数字“缩位”处理:就是把每个位的数字相加,得出的数字如果不是一位数字,就再缩位,直到变成一位数字为止。例如: 228 => 2+2+8=12 => 1+2=3 上面的数字缩位后变为:344836, 这就是程序最终的输出结果! 要求程序从标准输入接收数据,在标准输出上输出结果。 输入格式为:第一行是一个整数n(<100),表示下边有多少输入行,接下来是n行字符串,就是等待变换的字符串。 例如,输入: 则输出: 题目链接 非常简单的模拟题。。 按照下面两步走即可: 解题效率:解题思路
解题代码
#include 15.试题 算法训练 最小乘积(基本型)
题目
请调整每组数的排列顺序,使得两组数据相同下标元素对应相乘,然后相加的和最小。要求程序输出这个最小值。
例如两组数分别为:1 3 -5和-2 4 1
(-5) * 4 + 3 * (-2) + 1 * 1 = -25
n<=8,T<=10002
3
1 3 -5
-2 4 1
5
1 2 3 4 5
1 0 1 0 1
-25
6
解题思路
解题代码
#include 16.试题 算法训练 矩阵运算
题目
接下来n行,每行n个整数,表示A中的每一个元素。每个元素的绝对值不超过10000。
1 2 3
4 5 6
7 8 9
6 10 14
10 14 18解题思路
解题代码
#include 17.试题 算法训练 百鸡百钱
题目
例如 :
0 25 75
4 18 78解题分析
解题代码
#include 18.试题 算法训练 数据传递加密
题目
题目解析
解题代码
#include 二、算法提高
19. 试题 算法提高 心形
题目
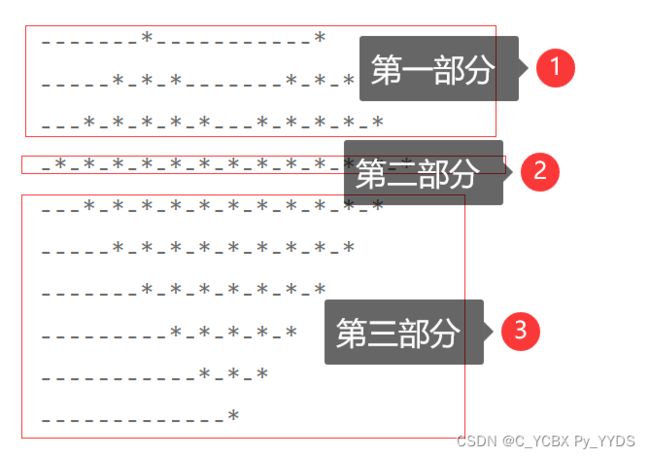
题目解析
" "(两个空格)称为空白元素 2. " *"(一个空格一个星)称为星元素。
后续这部分元素都以每次递减一个的趋势。
*所以起始元素长度为:1+(deep-1)2 ,而后续以每次递减2个的趋势。
解题代码
#include 20.试题 算法提高 字符串查找
题目
如a=“hello world”,b=“world”时,b第一次出现是在a的第7个字符到第11个字符,按照C++的习惯,位置从0开始编号,所以b在a中第一次出现的位置为6。
world
tsinsen题目解析
int n = 0;while (b[n]!=0)n++;//计算b的长度
int i=0,j;
while (a[i]!=0){
j = 0;
while (b[j]!=0){
if(a[i+j]!=b[j]){
break;
}
j++;
}
if(j==n){
return i;
}
i++;
}
return -1;
解题代码
#include #include 21.试题 算法提高 校门外的树
题目
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已 知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树 都移走后,马路上还有多少棵树。
150 300
100 200
470 471
对于其它的数据,区域之间有重合的情况。解题思路
解题代码
#include 22.试题 算法提高 第二大整数
题目
输入格式:输入只有一行,包括若干个整数,中间用空格隔开,最后一个整数为0。
输出格式:输出第二大的那个整数。
输入输出样例解题分析
解题代码
#include 三、历届试题
23.四平方和【第七届】【省赛】【C组】
题目
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去,就正好可以表示为4个数的平方和。
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
(^符号表示乘方的意思)
要求你对4个数排序:
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法
要求输出4个非负整数,按从小到大排序,中间用空格分开
5
则程序应该输出:
0 0 1 2
12
则程序应该输出:
0 2 2 2
773535
则程序应该输出:
1 1 267 838
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 3000ms
注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。题目解析
#include
解题代码
#include 24.历届真题 错误票据【第四届】【省赛】【B组】
题目
接着读入N行数据。
每行数据长度不等,是用空格分开的若干个(不大于100个)正整数(不大于100000)
每个整数代表一个ID号。
其中,m表示断号ID,n表示重号ID
用户输入:
2
5 6 8 11 9
10 12 9
7 9
用户输入:
6
164 178 108 109 180 155 141 159 104 182 179 118 137 184 115 124 125 129 168 196
172 189 127 107 112 192 103 131 133 169 158
128 102 110 148 139 157 140 195 197
185 152 135 106 123 173 122 136 174 191 145 116 151 143 175 120 161 134 162 190
149 138 142 146 199 126 165 156 153 193 144 166 170 121 171 132 101 194 187 188
113 130 176 154 177 120 117 150 114 183 186 181 100 163 160 167 147 198 111 119
105 120
峰值内存消耗 < 64M
CPU消耗 < 1000ms
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include , 不能通过工程设置而省略常用头文件。题目解析
一、cin输入的时候在输入缓冲区会留下一个换行符没有读取 '\n',而getline对于数据读取是碰到换行符就结束,所以在用getline读取一行之前我们需要掉用cin.ignore()把换行符给处理掉,否则会导致getline无法读入数据!
二、stringsteam类每次读入且完全被写出的时候,需要重新调用clear()来刷新缓冲区才能够进行下一次的读入写出!解题代码
#include 25. 历届真题 密码发生器【第三届】【省赛】【本科组】
题目
wangxi
ming
228 202 220 206 120 105
输出格式为:n行变换后的6位密码。
5
zhangfeng
wangximing
jiujingfazi
woaibeijingtiananmen
haohaoxuexi
772243
344836
297332
716652
875843。题目解析
解题代码
#include