数据结构 线段树--权值线段树 详解

| Powered By HeartFireY | Weighted Segment Tree

一、权值线段树 简介

1.线段树

线段树是一种用于维护区间信息的高效数据结构，可以在 $O(\log N)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树维护的信息必须满足可加性，即能以可以接受的速度合并信息和修改信息，包括在使用Lazy标记时，标记也要满足可加性

具体有关线段树的的讲解请参考博客：线段树 详解与模板

2.权值线段树

权值线段树是一种建立在基本线段树之上的数据结构。因此它的基本原理仍是基于对区间的维护操作。但与线段树相区分的点是：权值线段树维护的信息与基本线段树有所差异：

• 基本线段树中每个系欸但用来维护一段区间的最大值或总和等；
• 权值线段树每个结点维护的是一个区间的数出现的次数。

实际上，权值线段树可以看作是一个桶，桶的操作它都支持，并且能够以更快的方式去完成。

根据权值线段树的性质，我们可以知道其主要用途：

权值线段树一般用于维护一段区间的数出现的次数，从它的定义来看，它可以快速计算出一段区间的数的出现次数。

在实际应用中，我们使用权值线段树查询区间第$K$大的值。

二、权值线段树的基本原理与操作

1.权值线段树维护信息的原理

基础线段树和权值线段树的一个较大的区别点在于：(此处特指使用数组储存树结构)基础线段树根据初始的一个序列建立树结构，具有单独的建树操作；而权值线段树不需要进行建树操作，初始状态下默认建立一棵所有点权为$0$的空树，对于每个元素，在遍历的时候相应的结点做自增运算。换而言之：

• 权值线段是一棵已经建好的线段树，储存树结构的下标范围根据区间最大值最小值确定(一般开大空间即可)；
• 初始状态下所有的点权均为$0$；
• 执行插入元素的操作时，会导致插入值$v$对应的$A[v]++$，同时引发单点更新操作。
• 可以从上述描述中得到基本推论：向空的权值线段树中插入一个无序序列，则插入完成后在树上无法再得到原序列的遍历，但能通过遍历得到有序序列(无序序列变有序序列)

我们可以通过结构对比线段树与权值线段树的区别，以此理解原理。

我们给定序列$\{1,2,2,3,3,3,4,4,4,4\}$，以该序列为例建立两种线段树。

首先，序列长度为$10$，建立基础区间和查询线段树，结构图如下：

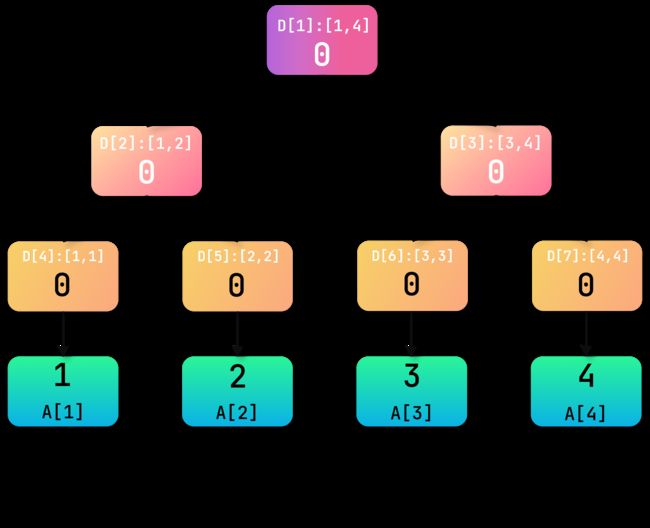
对应具体的细节不再阐述。我们继续建立权值线段树：首先给出一棵空树：

(注：为演示方便，A数组下标做+1操作，树上的范围也对应变化，这里懒得改了~)

然后按照序列顺序插入元素：

解释：

$A[1]=1$：原序列中存在值为$1$的元素$1$个
$A[2]=1$：原序列中存在值为$2$的元素$2$个
$A[3]=1$：原序列中存在值为$3$的元素$3$个
$A[4]=1$：原序列中存在值为$4$的元素$4$个

$D[k]$：一定区间内所含元素的个数

我们继续探究查找第$K$大元素的方法：

由于权值线段树每个节点记录了某段区间内包含的元素个数，且元素在叶子节点构成的序列中是有序的：

• 对于整列数中第$K$大/小的值，我们从根节点开始判断（这里按第$K$大为例），如果$K$比右儿子大，就说明第$K$大的数在左儿子所表示的值域中。然后，$K$要减去右儿子。（这是因为继续递归下去的时候，正确答案，整个区间的第$K$大已经不再是左儿子表示区间的第$K$大了)。如此递归到叶子节点时即为答案。
• 整棵线段树的根节点就表示整个值域有几个数。

我们很容易看出：在权值线段树中，采用元素到下标数组映射的方式进行插入。这样会导致一个问题：在数据离散程度较大的情况下，空间的利用效率比较低。因此我们对于线段树所开空间不足时，常采用离散化的方式进行解决。

| 此处的前导知识：离散化(具体的参见离散化的讲解)

2.权值线段树的基本操作与实现

①.查询第$K$大/小元素

假设$K=5$，那么查询过程是怎样的？

首先我们从根节点出发，由于要查询第$K$大，是相对于终点而言的，因此从右子结点开始判断：

当前节点右子树包含$4$个元素，所以应该向左子树遍历，注意：此时应该减去右子树的$4$个元素！

寻找第$K$小的操作与上方类似，区别在于相对于起点OR终点而言(遍历时对左右子树的判断顺序)。

再次回顾整个步骤：对于整列数中第$K$大/小的值，我们从根节点开始判断（这里按第$K$大为例），如果$K$比右儿子大，就说明第$K$大的数在左子树中。然后，$K$要减去右子节点的值。（这是因为继续递归下去的时候，正确答案，整个区间的第$K$大已经不再是左子树表示区间的第$K$大了)。如此递归到叶子节点时即为答案

根据以上分析步骤，我们可以写出查询第$K$大和第$K$小的函数：

int query_kth(int pos, int l, int r, int k){
    if(l == r) return l;
    int mid = (l + r) >> 1, right = tree[pos << 1 | 1];
    if(k <= right) return query(pos << 1 | 1, mid + 1, r, k);
    else return query(pos << 1, l, mid, k - right);
}

int query_kth(int pos, int l, int r, int k){
    if(l == r) return l;
    int mid = (l + r) >> 1, left = tree[pos << 1];
    if(k <= left) return query(pos << 1, l, mid, k - left);
    else return query(pos << 1 | 1, mid + 1, r, k);
}

②.单点更新操作

类似基础线段树，递归到叶子节点$+1$然后回溯

void add(int l, int r, int v, int x){
    if (l == r) tree[v]++;
    else{
        int mid = (l + r) >> 1;
        if (x <= mid) add(l, mid, v << 1, x);
        else add(mid + 1, r, v << 1 | 1, x);
        tree[v] = tree[v << 1] + tree[v << 1 | 1];
    }
}

③.查询某个数出现的个数

树上二分查找的思想，代码如下：

int find(int l, int r, int v, int x){
    if (l == r) return tree[v];
    else{
        int mid = (l + r) >> 1;
        if (x <= mid) return find(l, mid, v << 1, x);
        else return find(mid + 1, r, v << 1 | 1, x);
    }
}

④.查询一段区间的数出现的次数

int find(int l, int r, int v, int x, int y){
    if (l == x && r == y) return tree[v];
    else{
        int mid = (l + r) >> 1;
        if (y <= mid) return find(l, mid, v << 1, x, y);
        else if (x > mid) return find(mid + 1, r, v << 1 | 1, x, y);
        else return find(l, mid, v << 1, x, mid) + find(mid + 1, r, v << 1 | 1, mid + 1, y);
    }
}

3.区间离散化

如前所述，在将元素个数映射到叶子节点的过程中，离散程度较大时会导致极低的空间利用效率。对本种数据结构，我们关心的仅仅是元素之间的大小关系，因此可以采用离散化的方法对空间进行优化。

离散化的知识在此不展开赘述，直接采用C++STL算法

int get_discretization(){
    for (int i = 1; i <= n; ++i) a[i] = read(), b[i] = a[i]; //读入数据
    sort(b + 1, b + n + 1);
    int len = unique(b + 1, b + n + 1) - b - 1;
    for (int i = 1; i <= n; ++i){
        int pos = lower_bound(b + 1, b + len + 1, a[i]) - b;
        a[i] = pos;
    } //离散化
}