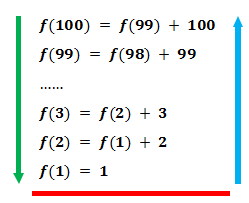【数据结构与算法Java(递归)】
递归
- 递归定义
-
- 递归练习
-
- 1.前n项求和
- 2.斐波那契数列
- 分治算法
-
- 定义
- 经典案例学习
-
- 全排列
- 迷宫问题
- 八皇后问题
递归定义
程序调用自身的编程技巧称为递归。
它通常将一个大型复杂的问题进行层层转化为一个与原问题相似的规模较小的问题进行求解。它的优点是代码量少,因为它是将复杂的大型问题分隔成多个相似的小型问题,大大的减少了代码量。
递归它需要有边界条件,递归前进段和递归返回段。若是边界不满足时,递归前进;当边界条件满足时,则递归返回。
递归练习
1.前n项求和
public class Demo01 {
public static void main(String[] args) {
System.out.println(sum(100));
}
public static int sum(int num){
if(num == 1){//边界条件
return 1;
}
return sum(num-1)+num;
}
}
2.斐波那契数列
斐波那契数列为 1,1,2,3,5,8,13,21……
它的第一项和第二项均为1,其余项为前两项之和。
package digui;
public class Demo01 {
public static void main(String[] args) {
System.out.println(fab(10));
}
public static int fab(int num){
if(num == 1 || num == 2){//边界条件
return 1;
}
return fab(num-1)+fab(num-2);
}
}
分治算法
定义
分治算法由两部分组成,分与治;分就是递归解决较小的问题;而治是从子问题的解构建原问题的解。
分治算法的递归实现中,每一层递归都会涉及三个操作:
1.分解:将原问题分解成一系列子问题;
2.解决:递归地求解每个子问题,若是子问题足够小,直接求解。
3.合并:将子问题的结果合并成原问题。
可以用分治算法解决的问题一般需要满足这些条件:
1.原问题与分解成的小问题具有相同的模式;
2.原问题分解成的子问题可以独立求解,子问题之间没有相关性。
3.具有分解终止条件,就是当问题足够小时,可以直接求解。
4.可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了。
经典案例学习
处理汉诺塔问题,我们可以将多个盘子分为两部分,假设有64个,第一部分是第64个,第二部分是前63个;我们需要先将前63个盘子通过辅助轴移动,然后才能将第64个盘子移动到目标位置;对于前63,我们也是分为第63个和前62个盘子;下面是栈的操作分析:
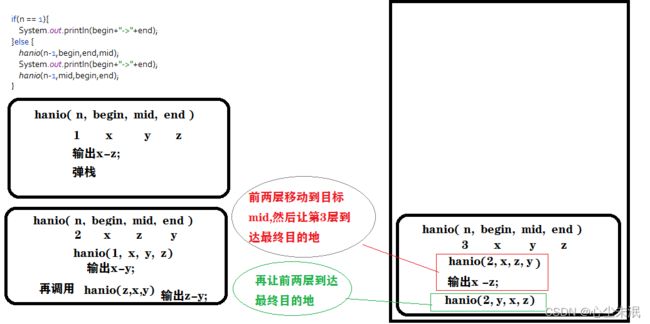
代码:
package digui;
public class Hanio {
public static void main(String[] args) {
String x = "X";
String y = "Y";
String z = "Z";
hanio(3,x,y,z);
}
private static void hanio(int n, String begin, String mid, String end) {
if(n == 1){
System.out.println(begin+"->"+end);
}else {
hanio(n-1,begin,end,mid);
System.out.println(begin+"->"+end);
hanio(n-1,mid,begin,end);
}
}
}
全排列
求所给字符串“ABC”的全排列,不包含重复;
分析:在全排列实现方法中,我们先后交换
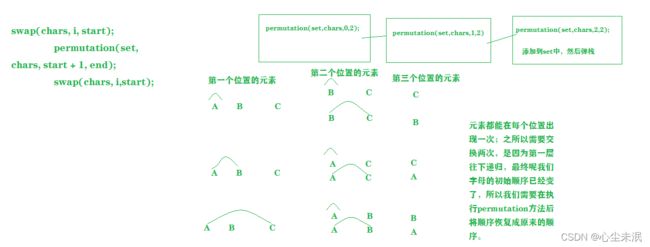
import java.util.HashSet;
public class QuanPai {
public static void main(String[] args) {
String str = "ABC";
//将所给字符串变成字符数组;
char[] chars = str.toCharArray();
//使用set进行去重操作
HashSet<String> set = new HashSet<>();
permutation( set,chars,0,chars.length-1);
System.out.println(set.toString());
}
private static void permutation(HashSet<String> set,char[] chars, int start, int end) {
if(start == end){
set.add(String.valueOf(chars));
}else {
for (int i = start; i <= end; i++) {
swap(chars, i, start);
permutation(set, chars, start + 1, end);
swap(chars, i,start);
}
}
}
private static void swap(char[] chars, int i, int start) {
char temp = chars[i];
chars[i] = chars[start];
chars[start] = temp;
}
}
迷宫问题
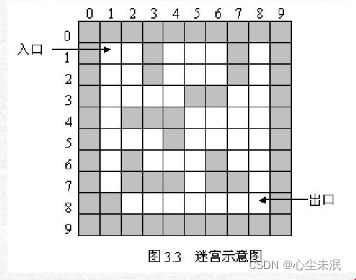
迷宫问题就是我们从一个口进,通过一系列操作找到出口的过程;在这我们是通过二维数组模仿的,路设置值为0;墙设置值为1;符合条件的路径坐标放在栈中;
代码
import lianbiao.LinkedList;
public class Maze {
private static int entryX = 1;
private static int entryY = 0;
private static int outX = 7;
private static int outY = 8;
//设置每个位置的状态是否已访问;
private static boolean visited[][] = new boolean[9][9];
//代表方向的数组;
private static int[][] direction = {
{-1,0},{0,1},{1,0},{0,-1}
};
private static int[][] maze = {
{1, 1, 1, 1, 1, 1, 1, 1, 1},
{0, 0, 1, 0, 0, 0, 1, 1, 1},
{1, 0, 1, 1, 1, 0, 1, 1, 1},
{1, 0, 0, 1, 0, 0, 1, 1, 1},
{1, 1, 0, 1, 1, 0, 0, 0, 1},
{1, 0, 0, 0, 0, 0, 1, 0, 1},
{1, 0, 1, 1, 1, 0, 0, 0, 1},
{1, 1, 0, 0, 0, 0, 1, 0, 0},
{1, 1, 1, 1, 1, 1, 1, 1, 1}
};
public static void main(String[] args) {
boolean flag = go(entryX,entryY);
if(flag){
for(String path : stack){
System.out.println(path);
}
}else{
System.out.println("迷宫不通!");
}
}
private static LinkedList<String> stack = new LinkedList<>();
private static boolean go(int X, int Y) {
//将该位置进行压栈,然后将其设置为已访问;
stack.push("("+X+","+Y+")");
visited[X][Y] = true;
//在进行下一个找路操作前先判断是否已找到出口;
if(X == outX && Y == outY){
return true;
}
//找路操作,遍历方向数组,按顺序进行每个方向的判断,是否可以前进。
for(int i = 0;i< direction.length;i++){
int newX = direction[i][0] + X;
int newY = direction[i][1] + Y;
if(InArea(newX,newY) && isRoad(newX,newY) && !visited[newX][newY]){
if(go(newX,newY)){
return true;
}
}
}
//将压栈的错误路径出栈,并返回false,表示次路不通,请换方向;
stack.pop();
return false;
}
private static boolean InArea(int newX, int newY) {
return newX>=0 && newX < 9 && newY >=0 && newY < 9;
}
private static boolean isRoad(int newX, int newY) {
return maze[newX][newY] == 0;
}
}
八皇后问题

八皇后问题就是一行放一个皇后,在一个位置放置皇后后,在下一行放置时,有条件约束,就是在它的正上方,左上方,右上方是不能放置的。然后找到所有的解。
代码
public class NQueen {
private static int count = 0;//解的个数
private static final int N = 8;//棋盘大小
private static int[][] arr = new int[N][N];//棋盘数据
public static void main(String[] args) {
queen(0);
}
//递归解决第row角标行皇后的问题。row=n;就是一个解
private static void queen(int row) {
if(row == N){
count++;
System.out.println("第"+count+"个解:");
printArr();
}else{
//遍历当前行的列;
for(int col = 0;col<N;col++){
if(!isDangerous(row,col)){
//每次要放置皇后的时候,需要先将同行清空
for(int c = 0;c<N;c++){
arr[row][c] = 0;
}
arr[row][col] = 1;
queen(row+1);
}
}
}
}
//判断该位置是否能放置皇后;
private static boolean isDangerous(int row, int col) {
//正上方
for(int r = row-1;r>=0;r--){
if(arr[r][col] == 1){
return true;
}
}
//左上方(对角线)
for(int r = row -1,c=col-1;r>=0&&c >=0;r--,c--){
if(arr[r][c] == 1){
return true;
}
}
//右上方(对角线)
for(int r=row-1,c=col+1;r>=0&&c<N;r--,c++){
if(arr[r][c] == 1){
return true;
}
}
return false;
}
private static void printArr() {
for(int i=0;i<N;i++){
for(int j=0;j<N;j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
}