LeetCode 958. 二叉树的完全性检验【c++/java详细题解】

1、题目

给定一个二叉树，确定它是否是一个完全二叉树。

百度百科中对完全二叉树的定义如下：

若设二叉树的深度为 h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。（注：第 h 层可能包含 1~ $2^h$ 个节点。）

示例 1：

输入：[1,2,3,4,5,6]
输出：true
解释：最后一层前的每一层都是满的（即，结点值为 {1} 和 {2,3} 的两层），且最后一层中的所有结点（{4,5,6}）都尽可能地向左。

示例 2：

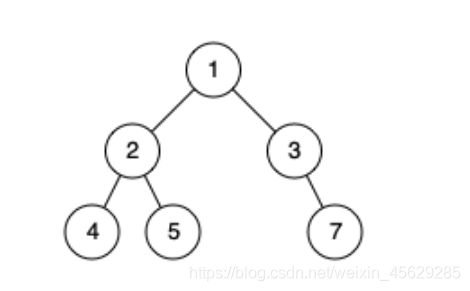
输入：[1,2,3,4,5,null,7]
输出：false
解释：值为 7 的结点没有尽可能靠向左侧。

提示：

1. 树中将会有 1 到 100个结点。

2、思路

(dfs) $O(n)$

完全二叉树的堆式存贮，堆就是一个完全二叉树，而完全二叉树可以用数组表示。我们将一个值为1~n的连续数组表示成一个完全二叉树如下图所示：

在完全二叉树中，用 1 表示根节点编号，则对于任意一个节点 x，它的左孩子为 2*x，右孩子为 2*x + 1 。那么我们可以发现，一颗二叉树是完全二叉树当且仅当节点编号依次为 1, 2, 3, ...n 且没有间隙。换句话说，可以将其表示为一个值为1~n的连续数组。而在一个值从1开始的连续数组中，数组中最大元素值等于数组大小。 在根节点编号值为1的完全二叉树则是，节点编号最大值等于节点个数。

因此，我们可以对一颗二叉树进行dfs搜索，如果搜索出的节点编号序列值恰好可以组成一个升序的数组并且编号序列是一个从1开始的无间隔的连续数组，则该二叉树为完全二叉树。

递归函数设计：

bool dfs(TreeNode* root , int k) //k是当前节点编号

root是当前遍历的节点，k是当前节点编号。

搜索过程如下：

• 1、我们从根节点开始搜索，并将根节点编号值设置为1。
• 2、然后搜索左子树，并传递其根节点值为2*k。搜索右子树，并传递其根节点值为2*k+1
• 3、在递归搜索过程中，记录节点个数n和当前最大节点编号值p。
• 4、最后判断最大节点值p和节点数n是否相等，相等则该二叉树是完全二叉树，否则不是。

递归边界：

• 1、题目规定树中最多有100个节点，如果节点编号k > 100，说明该二叉树不合法，返回false。
• 2、递归到叶子节点，子树递归结束，返回true。

时间复杂度分析： $O(n)$，其中 $n$是树节点个数 。

3、c++代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int n = 0, p = 0;  //n是节点数，p是最大节点编号值
    bool isCompleteTree(TreeNode* root) {
        if(!dfs(root,1)) return false; //还没有递归到终点就返回false，说明其不是完全二叉树
        return n == p;  //判断最大节点值是否和节点数相等
    }
    bool dfs(TreeNode* root , int k) //k是当前节点编号
    {
        if(!root) return true;  //递归到了叶子节点
        if(k > 100) return false;
        n++, p = max(p,k); //记录节点数和最大节点编号值
        return dfs(root->left,2*k)&&dfs(root->right,2*k + 1); //递归左右子树
    }
}; 

4、java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int n = 0, p = 0; 
    public boolean isCompleteTree(TreeNode root) {
        if(!dfs(root,1)) return false;
        return n == p;
    }
    public boolean dfs(TreeNode root , int k) //k是当前节点编号
    {
        if(root == null) return true;  //递归到了叶子节点
        if(k > 100) return false;
        n++;  p = Math.max(p,k); //记录节点数和最大节点编号值
        return dfs(root.left,2*k)&&dfs(root.right,2*k + 1); //递归左右子树
    }
}

原题链接： 958. 二叉树的完全性检验