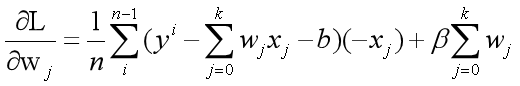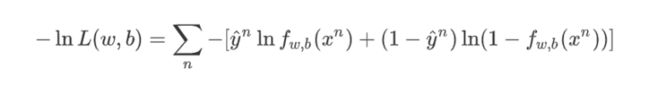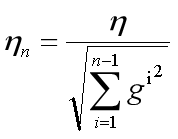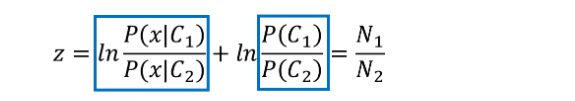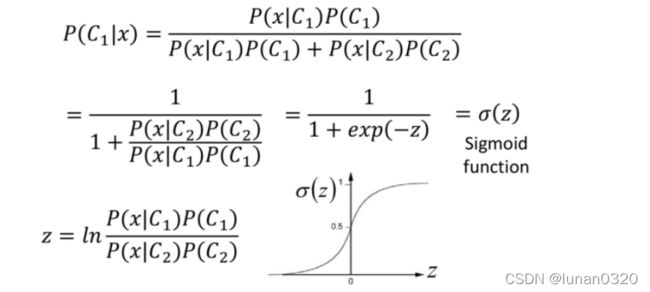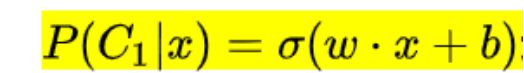机器学习实验二（李宏毅-判断年收入）

机器学习 Lab2 实验报告

欢迎大家访问我的GitHub博客

https://lunan0320.github.io/

一、实验目的

  掌握Classification中的生成模型generative model以及logistic regression model。
  掌握二分类问题的机器学习方法，根据已有数据，判断该人年收入是否大于5万美元。

二、实验要求及环境

2.1 实验要求

1、不可以使用tensorflow或者pytorch库
2、可以使用pandas库读取csv文件数据信息(其他库亦可)
3、使用概率生成模型解决问题
4、使用logistic regression解决问题
5、概率生成模型可以完善给出代码，也可自行完成

2.2实验环境

戴尔G3游匣 Intel core i7 Windows10
Python3.8 PyCharm

三、设计思想

3.1 文件描述

  train.csv：3256115的表格，每一行有15个情况，其中最后一列是年收入的情况。
  X_train：32561106的表格。是对train.csv文件通过one-hot方法处理之后的文件。对每一个行有106个特征，其中106是将前14种属性值展开后的结果，代表了age, workclass, fnlwgt (总人数), education, education num, marital-status, occupation, relationship, race, sex, capital-gain, capital-loss, hours-per-week, native-country, make over 50K a year or not。
  Y_train:325611的表格。是对train.csv文件通过one-hot方法处理之后的结果。每一行只有一个特征，就是年收入。其中，年收入小于50k，则赋予label 0，否则赋予label 1。
  test.csv: 1628114的表格。是需要通过训练后的模型去计算各自对应的年收入值。
  X_test:16281*106的表格。是对test.csv文件通过one-hot方法处理之后的结果。

3.2 模型方法

3.2.1 Gaussian Distribution

3.2.2偏微分计算

3.2.3 Logistic Regression

3.2.4 Loss function（Cross Entropy）

3.2.5 Adagrad过程

3.3模型构想

3.3.1 模型一：补充代码Generative model

3.3.2 模型二：自行完成Generative model

3.3.3 模型三：logistic regression

四、模型一

  使用生成模型，generative model来处理问题
  代码及数据见文件：generative补充代码.py output.csv

4.1数据读取及预处理

  观察后发现，给出的代码是采用了类的方式处理过程，因此直接在总类data_manager()之下完成补充函数即可。

  首先需要将三个通过one-hot方法处理之后的文件读取出来，对X_train、Y_train、X_test分别读取。
  观察之后发现没有格式不正确、不合规的数字，因此直接对文件进行读取处理。
  读取的过程中需要对首行进行过滤，此处是使用了切片的方式将文件的内容以浮点float的类型读取出来，rows即是读取到的数组。

  读取出数据之后，由于每个特征数据的分布情况是不同的，因此需要对数据进行标准化处理，对数据标准化处理可以使得数据的结果不会受某个特征的影响太大或者太小，此处是使用了正态分布的标准化处理方式。
  对于标准化，如果是X_train文件则使用numpy的函数mean求均值，使用std函数求方差，同时将其均转化为一行的shape，即转化之后计算得到的mean和std均是1*106的数组格式。
  依次对rows的每一行进行标准化遍历。对每一行执行正太分布标准化的方式进行。即可完成。

  对于X_test的标准化，则是使用X_train的中得到的均值和方差，也就是类中的self.mean和self.std，直接使用标准化方法即可。

  最后将结果索引到data[name]中。

4.2参数的计算

4.2.1 对训练数据分类

将训练数据分为两类，class_0和class_1。分类的方法是去遍历Y_train中的元素，如果说等于0，则将下标索引加入到class_0_id中。否则就将它加入到class_1_id中。
接着需要在X_train中找到这些下标对应的值，并将其作为对应的class。

4.2.2 计算均值和协方差

  此处假设服从的是高斯分布Gaussian Distribution。推到过程使用极大似然估计法。

  最优的均值和协方差的计算直接使用推导的最后的公式即可。

  使用numpy的库函数，mean()方法，对每一列求均值，对两个class分别得到对应的均值mean_0和mean_1，均是1*106的数组。

  协方差的计算即是实际值与均值差的平方，此处由于是矩阵形式，需要先转置后矩阵相乘。
  首先是对两个类的协方差的初始化。
  此处的n其实就是整个的维度，也就是特征值的数量。

  矩阵相乘使用了numpy中的dot（）方法。对每一行依次计算，得到的分别是两个类的106*106的协方差矩阵。
  计算得到的N0和N1是两个中元素的数量，即行数。
  最后求得协方差需要除以类中的行数。

  为了使得模型更加完善，此处使用了两个类共享一个协方差的方法。
  对两个计算得到的协方差加权平均即可。

4.2.3 计算w和b

  对z的推导过程如下

  对z 的计算即可得到如下结果：

  经过化简之后，得到如下的表达式。可以看到前面是个一次项，后面是个常数项。
  这就类似于线性回归中的w*x+b的方法。因此，在求后验概率的时候就需要先求得w和b这两个参数。

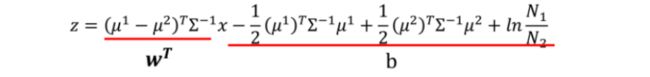
  此处，对于w和b而言，所有的项都已知，只是需要先对协方差求逆运算。

  因此，对于w和b的求取只需要将相应的参数代入即可。过程如下。

  求得w和b之后需要计算得到z，并使得其过一次sigmoid（）函数，得到结果位于0-1之间的对y的预测值。

  其中sigmoid函数的定义是已经有公式给出的。

  func函数的实现过程如下。对x的每一行分别计算其z的取值，根据sigmoid()函数，求得界于0-1之间的预测值。

  接着需要用这些得到的界于0-1之间的过sigmoid（）函数的值去预测y。

预测函数即是对求得的result取整规化为0和1的过程。

4.3准确率的计算

  为了考察模型的准确率，此时需要将模型计算得到的预测值与实际的Y_train文件的值求绝对差的平均值。也就是计算了错误率。
  准确率的计算需要在此基础上用1减去错误率即可。

4.4 X_test的预测

  在建立好模型，得到相关参数数据之后，需要使用该模型去预测未知量。对给定的X_test文件预测其年收入情况。
  result是对X_test的每一行过一次sigmoid()函数之后得到的界于0-1之间的数据。answer是对result的整数化的结果。也就是说answer就是最终的预测值。

  最后将预测值以特定的格式按行写入output.csv文件中。

4.4 模型建立并预测过程

1、创建类

2、文件读取与预处理

3、参数计算

4、预测数据并写入文件

五、模型二

使用生成模型，generative model来处理问题（自行完成的生成模型）
代码见文件：generative自己完成.py
数据见文件：Y_predict_generative.csv

5.1数据读取及预处理

  首先需要将三个通过one-hot方法处理之后的文件读取出来，对X_train、Y_train、X_test分别读取。
  观察之后发现没有格式不正确、不合规的数字，因此直接对文件进行读取处理。
  读取时候使用的方法是使用pandas库的方法读取csv文件，此处需要注意的是因为文件的首行是特征的名称集合，因此需要设置header=0的方式跳过首行。

  将读取到的文件内容通过numpy库函数转换为数组格式。并将该数组data返回。

  对数据的读取，分别调用data_read()函数对处理后的数据读取。

  对数据进行归一化处理，此处需要对X_train和X_test分别归一化。

将x_train和x_test使用numpy的concatenate()函数，将二者统一处理。求出x_all的均值和方差，对x_all实行正态分布的标准化处理方法，

  此处得到的x_mean和x_std是1*106的一维数组，为了实现更加方便的数组之间直接进行运算，需要将x_mean和x_std数组扩展为和x_all在第一维度同维度的数组。  在扩展过程中，使用的是numpy的tile函数。
  得到扩展后的x_mean和x_std之后就可以对数据进行标准化。

  对整体进行标准化之后，再将整体数据分为x_train和x_test数据即可。此时得到的x_train和x_test即是统一标准化之后的结果。

5.2 训练集与验证集分割

  对于X_train和Y_train数据需要进行分割，分为训练集和验证集两部分。其中，训练集用于模型的学习，验证集用于模型准确率的验证。

  分割的时候需要提前设置分割比例。此处设置比率为0.9，即是训练集：验证集=9：1

  为了使得验证集和训练集的选取更加随机，而不是直接选择前面的若干行为验证集或训练集，此处在查阅资料之后了解到numpy的shuffle生成随机序列的函数。

  此处使用该函数对X和Y进行随机化处理。
  首先是生成一个随机序列，长度就是x的行数。
  接着对该随机序列调用shuffle函数，对随机序列随机化。
  最后让X和Y使用该随机序列的顺序，即可实现对X和Y数据的打乱。

  得到该随机序列之后即可得到一个随机化的X和Y。此时再取0.9的训练集，0.1的验证集就是一个很随机的情况了。
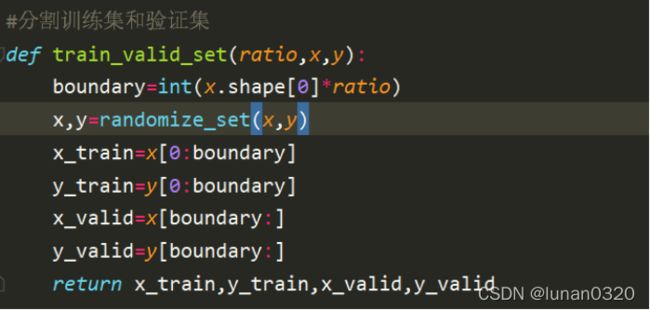
  为了使得序列直接取到前ratio的部分，设置了boundary界限。
  依次对x和y取出bounary的部分。返回值依次到x_rrain，y_train，x_valid、y_valid。即可实现对训练集和验证集的分隔。

5.3 计算均值和协方差

  此时需要求两个分类的均值u1、u2以及共用的cov协方差，两个类的元素数量N1、N2.

  首先需要进行分类，此处使用了比较快捷的方式，zip函数对X_train和Y_train进行打包处理。对于Y为1就归为第一类。对于Y为0则处理为第二类。

  使用numpy的求均值的mean方法，求出两个类的u1和u2

  计算N1和N2就是求出两个类的一维长度。也就是两个类的元素数量。

与模型一类似，代入相关数据，直接使用公式即可得到每个类的协方差。对协方差求加权平均，即可得到。

5.4计算w和b

  由于在求z的过程中需要求中间变量w和b。

  该过程需要用到协方差的逆，因此先对协方差求逆。

  同模型一类似，也是使用公式直接即可求得w和b。

5.5计算验证集的准确率

  在求得参数训练好模型之后，就可以使用验证集去验证一下准确率的大小。

对验证集求准确率即是先找到x_valid的预测值，过一次sigmoid()函数，求出界于0-1之间的数值。通过around函数四舍五入。

  此处为了避免由于数值太小，通过numpy的clip函数，将其转换为了界于1e-8和1-(1e-8)的数字。
  之后统计出现相同的频率即可找到其准确率。

5.6 X_test的预测

  在建立好模型，得到相关参数数据之后，需要使用该模型去预测未知量。对给定的X_test文件预测其年收入情况。

  对X_test进行预测，对X_test过sigmoid函数，并四舍五入，得到y_test，将y_test写入Y_predict_generative.csv文件。

  预测得到的结果如下：

5.7 模型建立并预测过程

1、首先数据处理，对x数据标准化
2、分割训练集和验证集
3、对训练集分类，求出每一类的u1、u2、cov
4、利用公式用u1、u2、cov求出w和b
5、用w、b过sigmoid函数，得到分类函数f
6、对验证集每个数过分类函数，得到验证的准确率
7、对test数据过分类函数，将输出以0、1格式输出到Y_predict_generative.csv文件中

六、模型三

使用生成模型，logistic Regression来处理问题
代码见文件：Logistic_Regression.py
数据见文件：Y_predict_logistic.csv

6.1数据读取及预处理

  首先需要将三个通过one-hot方法处理之后的文件读取出来，对X_train、Y_train、X_test分别读取。
  观察之后发现没有格式不正确、不合规的数字，因此直接对文件进行读取处理。
  将读取到的文件内容通过numpy库函数转换为数组格式。并将该数组data返回。

  对数据的读取，分别调用data_read()函数对处理后的数据读取。

  对数据进行归一化处理，此处需要对X_train和X_test分别归一化。

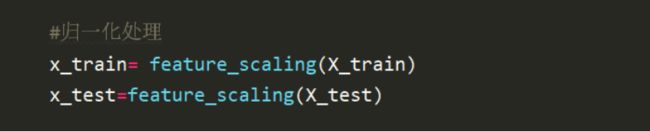
  将x_train和x_test分别调用该函数，求出均值和方差后，是1*106的数组，然后按列处理，对每一列依次进行标准化，此处+1e-8是因为为了避免出现异常问题。

6.2 训练集与验证集分割

  对于X_train和Y_train数据需要进行分割，分为训练集和验证集两部分。其中，训练集用于模型的学习，验证集用于模型准确率的验证。

  分割的时候需要提前设置分割比例。此处设置比率为0.9，即是训练集：验证集=9：1

  为了使得验证集和训练集的选取更加随机，而不是直接选择前面的若干行为验证集或训练集，此处与模型二类似使用的是numpy的shuffle生成随机序列的函数。

  得到该随机序列之后即可得到一个随机化的X和Y。此时再取0.9的训练集，0.1的验证集就是一个很随机的情况了。
为了使得序列直接取到前ratio的部分，设置了boundary界限。

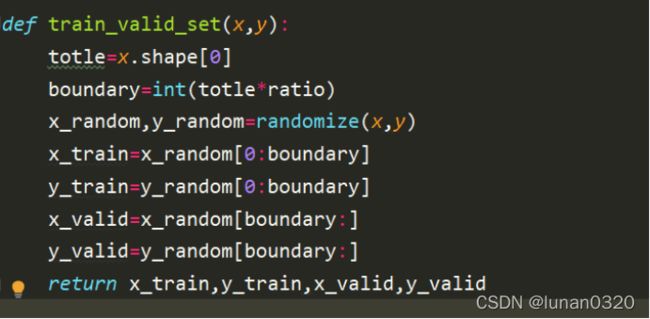
  依次对x和y取出bounary的部分。返回值依次到x_rrain，y_train，x_valid、y_valid。即可实现对训练集和验证集的分隔。

6.3 计算w和b

  Logistic_Regression使用的是直接求解w和b的方法，因此此处也直接使用的是Adagrad梯度下降的方法求解。

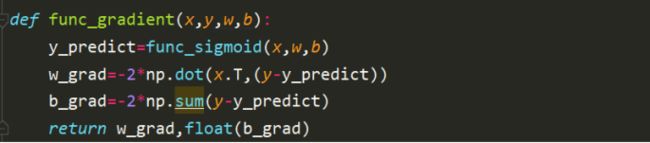
  由于梯度下降的数据量过大，因此，此处使用的是每10行更新一次的方法，初始化设置学习率lr=0.1。相当于是每10行为一个block处理，梯度下降的函数在上一个实验中已经完成过。

  类似的可以得到本模型的梯度下降函数。

  需要注意的是，此处的每次迭代是分块进行的，每一次的更新是以块为单位更新的。

6.4计算验证集的准确率

  在求得参数训练好模型之后，就可以使用验证集去验证一下准确率的大小。

对验证集求准确率即是先找到x_valid的预测值，过一次sigmoid()函数，求出界于0-1之间的数值。然后对该值利用求交叉熵cross_entropy的方法求得loss值。然后对预测的y通过around函数四舍五入。
  计算准确率的时候，需要求y和预测值之间的偏差的均值，也就是错误率。用1-错误率即可。得到验证集的准确率和交叉熵（loss）。

  此处为了避免由于数值太小，通过numpy的clip函数，将其转换为了界于1e-8和1-(1e-8)的数字。

6.5 X_test的预测

  在建立好模型，得到相关参数数据之后，需要使用该模型去预测未知量。对给定的X_test文件预测其年收入情况。

  对X_test进行预测，对X_test过sigmoid函数，并四舍五入，得到y_test，将y_test写入Y_predict_logistic.csv文件。

6.6 Regularization正则化的影响

  需要改动的地方是对w和b的求取，以及准确率和loss值的计算的地方。

  此时，需要对交叉熵重新计算。加入正则项。正则项的加入如图红色框线。

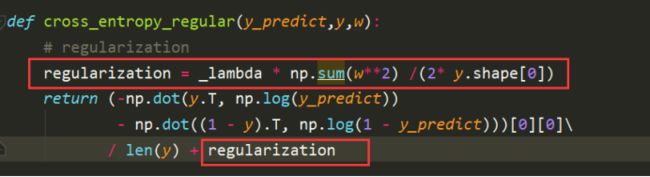
  重新计算w梯度，加入正则项。对每一列一次遍历，_lambda已在全局变量中给出。

6.7 验证集准确率分析比较

  此处给出的是迭代10次之后的结果。训练集设定的是9：1。可以看到，正则化之后并没有对验证集的准确率与交叉熵loss值有所改善。
  分析之后，发现此模型仍然是属于线性模型，没有高次项，而正则化是对高次项的过拟合现象有较好的改良，对于此处的线性模型其实优化效果一般。

6.8 影响最大的特征

  讨论哪个特征对实验结果的影响最大其实就是找出哪个特征对应的w的绝对值最大。
  在实验求得w和b之后，寻找w最大值所对应的特征即可。该特征即是影响因素最大的。

  从结果种可以看出，影响最大的特征是capital_gain，也就是资本收益对于收入能否大于50k是影响最大的。

七、模型评价

7.1优点

7.1.1、模型特征综合考虑

  为了得到模型的较优解，此处是直接计算了模型的全部特征，即使某个特征没有什么影响，也可以视为此处的w为0，这样就不容易错过一些有影响的特征，从而提高了模型的准确率。

7.1.2、分类之间共用协方差

为了提高模型的准确性，在生成模型Generative Model中对协方差是采取了共用的方式。

7.1.3、使用高阶Gradient方法

  在模型三Logistic Regression的过程中，使用了Adagrad作为主要求梯度的方法，使得学习率随着迭代次数动态变化。

7.1.4、Feature Scaling特征标准化

  使用归一化技术，使得消除了不同特征之间的影响，更容易收敛到最佳情况。

7.1.5、验证集均匀分布

  将训练集和验证集分割，而验证集又是充分随机选取，使得模型更容易推广，从而降低了test数据下的误差。

7.2缺点

7.2.1、未综合考虑多种迭代方式

  对于使用Logistic_Regression时，可以考虑采用多种迭代方式，在梯度下降的过程中，除了Adagrad之外，可以考虑SGD的放大，可以对比综合考虑。

7.2.2、考虑了部分无用特征

  考虑了部分无用特征，从总特征中可以看出，显然的是并非所有的特征都是有效的。对于没有用的特征其实是可以不考虑的，但是从求出的w可以看出，并没有哪一个特征对应的w为0的情况，都会或多或少的有一定的值。这就会将误差加入进去。

7.2.3、生成模型假设单一

  生成模型只考虑了假设其是服从高斯分布的情况，并没有考虑类似朴素贝叶斯（当然不可能是这个）等其他分布情况，因此这就使得假设直接按照Gaussian Distribution的过程进行，假设的条件单一。

7.2.4、Adagrad优化瓶颈

  虽然通过Adagrad方法使得不同的变量有了各自的学习率，但是初始情况的全局学习率需要自己指定。
  此时，如果设置的全局学习率过大，则优化一样是不稳定的；
  如果设置的全局学习率过小，则随着迭代过程的进行，根据Adagrad的学习特性，学习率可能会越来越小，很有可能在没有到达极值点的时候就已经是停滞不前的状态了。

八、实验心得

  在分类问题中可以类比回归模型的思路，尤其是在Logistic Regression中更是体会到了与回归的对比。
  在考虑特征值的时候并不一定是所有的特征值都有用，即使选取全部特征值，对于某些特征值的w可以为0，但是在实际训练情况中，几乎没有w为0的情况，或多或少均会引入误差。
  在本问题中使用生成模型求解和使用logistic regression求解的结果其实是差不多的，都是比较适合本问题的求解方法。
  对同一问题的解决过程，如果使用不同的模型，结果可能也是差不多的。但是在一些条件下，结果的差距可能是很大的。
  在Logistic Regression里面，是没有做任何实质性的假设，没有对Probability distribution有任何的描述，我们就是单纯地去找b和w。
  而在Generative model里面，对Probability distribution是有实质性的假设的，之前我们假设的是Gaussian(高斯分布)，甚至假设在相互独立的前提下是否可以是naive bayes(朴素贝叶斯)，根据这些假设我们才找到最终的b和w。
  Training Data和Validation Data要区分开，不能在训练集中直接选取一部分用来验证求loss值的大小。Training Data中用来训练模型，而Validation Data用来验证模型优劣，计算loss值。

九、参考文献

[1] [机器学习]正规化_for justice-CSDN博客_正规化
https://blog.csdn.net/jidong2622/article/details/79354332
[2] numpy.tile()
https://blog.csdn.net/qq_18433441/article/details/54897250
[3] 数组对象
https://www.numpy.org.cn/reference/arrays/
[4]numpy.random.shuffle打乱顺序函数
https://blog.csdn.net/jasonzzj/article/details/53932645
[5] Pandas手册
https://www.pypandas.cn/docs/getting_started/basics.html
[6] Adagrad 优化
https://www.jiqizhixin.com/graph/technologies/7eab38a3-23ec-494c-a677-415b6f85e6c5

十、提交文件注解

训练集：X_train Y_train
预测集：X_test
1、模型一：
代码 generative补充代码.py 数据 output.csv
2、模型二：
代码 generative.py 数据 Y_predict_generative.csv
3、模型三：
代码 Logistic_Regression.py 数据 Y_predict_logistic.csv