2020年第十一届蓝桥杯A组省赛

A.门牌制作（5分）
答案：624

分析：
送分题，直接遍历1~2020之间每一个数，分析该整数的每一位，计算2的个数。

#include
using namespace std;
int main(){
	int cnt=0;
	for(int i=1;i<=2020;i++){
		int x=i;
		while(x){
			if(x%10==2) cnt++;
			x/=10;
		}
	}
	cout<<cnt<<endl;
	return 0;
} 

---

B.既约分数（5分）
答案：2481215

分析：
考察最大公因数gcd的用法。 分子分母双重循环分别遍历1~2020之间的每一个数，判断分子和分母的最大公因数是否是1，若是1，则结果加一。

#include
using namespace std;
inline gcd(int a,int b){
	return b?gcd(b,a%b):a;
} 
int main(){
	int cnt=0,n=2020;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(gcd(i,j)==1) cnt++;
		}
	}
	cout<<cnt<<endl;
	return 0;
} 

---

C.蛇形填数（10分）
答案：761

分析：
很容易可以发现主对角线的元素是有规律的。 即从1，5，13, … 可知， 主对角线上的第i个元素比第i-1个元素大4 * (i-1)。要是不信，可以手动多写几个试试看。

#include
using namespace std;
int main(){
	int ans=1;
	for(int i=2;i<=20;i++){
		ans+=(i-1)*4;
	}
	cout<<ans<<endl;
	return 0;
} 

---

D.七段码(10分）
答案：80

分析：
递归枚举+并查集维护。由于数码管只有7段，每根数码管只有选和不选两种情况；所以所有可能的情况共有2^7=128种。 对于每种情况，我们借助并查集判断一下是否是连通的。由于并查集是一种将连通结点放在同一个连通块的方法，所以我们对于每条选中的边，需要将其结点合并。

#include
using namespace std;
bool vis[10];
int fa[10];
int u[10]={0,1,2,3,4,5,6,6};
int v[10]={0,2,3,4,5,6,1,3};
long long ans=0;
inline int find(int x){
	return x==fa[x]?x:fa[x]=find(fa[x]);
}
void Union(int u,int v){
	if(find(u)==find(v)) return ;
	fa[find(u)]=find(v);
}
void check(){
	int pos=0;
	for(int i=1;i<=6;i++) fa[i]=i;
	for(int i=1;i<=7;i++){
		if(vis[i]) {
			pos=u[i];
			Union(u[i],v[i]);
		}
	}
	if(!pos) return;
	for(int i=1;i<=7;i++){
		if(vis[i]) {
			if(find(u[i])!=find(pos)||find(v[i])!=find(pos)) return ;
		}
	}
	ans++;
}
void dfs(int x){
    if(x<=7){
    	vis[x]=true;  dfs(x+1);  //选第x根 
    	vis[x]=false; dfs(x+1); //不选第x根 
	}
	else check();
}
int main(){
	for(int i=1;i<=7;i++) vis[i]=false;
    dfs(1);
    cout<<ans<<endl;
	return 0;
} 

---

E.平面分割(15分）
答案：

分析：
对于一点立体想象能力都没有的我来说，还是放弃吧！！！

---

F.成绩分析(15分）

分析：
水题，水的一批。

#include
using namespace std;
#define INF 0x7fffffff
int main(){
	int maxx=-INF,minn=INF,n;
	double aver=0.0;
	cin>>n;
	for(int i=1;i<=n;i++){
		int x; cin>>x;
		maxx=max(maxx,x);
		minn=min(minn,x);
		aver+=x;
	}
	aver/=n;
	printf("%d\n%d\n%.2lf",maxx,minn,aver);
	return 0;
} 

---

G.回文日期(20分）

分析：
一道简单模拟题。由于数据范围是8位数的限制，在O(n)的时间复杂度下直接暴力便可求出结果。用一个数组yue[15]存1~12月的天数；然后对于每一年都需要判断是平年还是闰年，若是平年，则yue[2]=28,否则，yue[2]=29。 然后判断对于遍历到的某个数i，它的月份和日期是否规范；最后再判断他是否是回文数字，若是回文再判断它是否是ABABBABA型数字，用res1和res2分别记录结果即可。

#include
using namespace std;
#define INF 0x7fffffff
int yue[15]={0,31,28,31,30,31,30,31,31,30,31,30,31},a[10];
bool is_run(int year){
	if(year%400==0||(year%4==0&&year%100!=0)) return true;
	return false;
}
bool is_huiwen(int year,int month,int day){
     a[1]=year/1000;a[2]=(year/100)%10;a[3]=(year/10)%10;a[4]=year%10;
     a[5]=month/10;a[6]=month%10;a[7]=day/10;a[8]=day%10;
     for(int i=1;i<=4;i++) if(a[i]!=a[8-i+1]) return false;
	 return true; 
}
bool is_ABAB(){
	if(a[1]==a[3]&&a[3]==a[6]&&a[6]==a[8]&&a[2]==a[4]&&a[4]==a[5]&&a[5]==a[7]) return true;
	return false;
}
int main(){
	int n; cin>>n;
	int res1=0,res2=0;
	for(int i=n+1;i<=99999999;i++){
		int year=i/10000,month=(i/100)%100,day=i%100;
		if(is_run(year)) yue[2]=29; 
		else yue[2]=28;
		if(month>12||day>yue[month]) continue;
	    if(is_huiwen(year,month,day)){
		    if(!res1) res1=i; 
			if(!res2&&is_ABAB()) res2=i;
			if(res1&&res2) break;
		}
	}
	cout<<res1<<"\n"<<res2<<endl;
	return 0;
} 

---

H.子串分值（20分）

考场骗分做法：60分

思路：
观察输入的用例规模，会发现有一个60%的用例，n<=10000,显然恰好适合双重for循环暴力； 在考场实在没有完美方案的情况下暴力将是得分的好帮手。第一重循环遍历子串起点，第二重循环遍历子串终点，用标记数组vis[30]记录某一个字符出现次数，cnt记录子串str[i…j]的仅出现一次的字符个数，若某字符第一次出现，即vis[]=0,则标记为1，cnt++；若第二次出现，即vis[]=1,则标记为2,cnt - -。这样便能求出每一个子串的结果了，全部相加便是最后结果。

#include
using namespace std;
#define INF 0x7fffffff
const int maxn=1e5+100;
long long ans=0;
int main(){
	char str[maxn]; cin>>str;
	int n=strlen(str),vis[30]; 
    for(int i=0;i<n;i++){
    	int cnt=0;
    	memset(vis,0,sizeof(vis));
    	for(int j=i;j<n;j++){
    		if(!vis[str[j]-'a']) vis[str[j]-'a']=1,cnt++;
    		else if(vis[str[j]-'a']==1) cnt--,vis[str[j]-'a']=2;
    		ans+=cnt;
		}
	}
	cout<<ans<<endl;
	return 0;
} 

AC做法

思路：
对于第i个字符，我们记录它前面离它最近的一个相同字符的位置l[i]，若没有，初始化为0；再记录它后面离它最近的一个相同字符的位置r[i]，若没有，初始化为n+1。 对于第i个字符对最终结果的贡献有以下规律：
1. 它本身一个字符对答案有贡献值1.
2. 它到r[i]中间字符的个数tail（不包括它本身和r[i]），对答案有贡献值tail。
3. 它到l[i]中间字符的个数head（不包括它本身和l[i]），对答案有贡献值 head*tail+head。如何理解这部分呢？ 贡献值head与第二点一致。而对于贡献值head * tail来说，子串从head中任意一点出发，它到r[i]的贡献值都是tail。

#include
using namespace std;
#define INF 0x7fffffff
typedef long long ll;
const int maxn=1e5+100;
ll ans=0,n;
int l[maxn],r[maxn],vis[30];
void Init(){
	for(int i=0;i<n;i++) l[i]=0,r[i]=n+1;
} 
int main(){
	char str[maxn]; cin>>str;
	n=strlen(str); 
	Init(); memset(vis,0,sizeof(vis));
	for(int i=0;i<n;i++){
		if(!vis[str[i]-'a']) vis[str[i]-'a']=i+1;
		else l[i]=vis[str[i]-'a'],vis[str[i]-'a']=i+1;
	}
	memset(vis,0,sizeof(vis));
	for(int i=n-1;i>=0;i--){
		if(!vis[str[i]-'a']) vis[str[i]-'a']=i+1;
		else r[i]=vis[str[i]-'a'],vis[str[i]-'a']=i+1;
	}
	for(int i=0;i<n;i++){
	    int head=0,tail=0;
		tail=r[i]-i-2;
		head=i-l[i];
	    head=head*tail+head;
		ans+=head+tail+1;  		
	}
	cout<<ans<<endl;
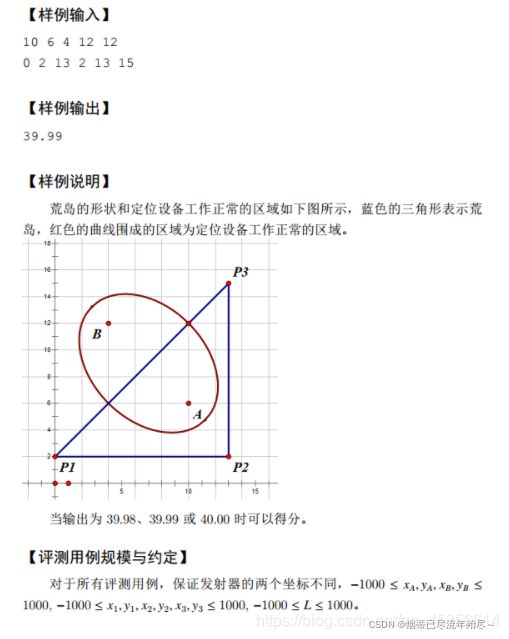
	return 0;
} 

---

I.荒岛探测（25分）

分析：

---

J.子串排序（25分）


考场骗分做法：30分

分析： 直接打表骗分，毕竟25*0.3=7.5分，可是相当于一道半的A题分值。当然如果时间允许，甚至还能搞到50%的样例。哈哈哈

#include
using namespace std;
#define INF 0x7fffffff
typedef long long ll;
const int maxn=1e5+100;
int main(){
    int n; cin>>n;
    if(n==1)  cout<<"ba"<<endl;
    else if(n==2) cout<<"baa"<<endl;
    else if(n==3) cout<<"cba"<<endl;
    else if(n==4) cout<<"bbaa"<<endl;
    else if(n==5) cout<<"cbaa"<<endl;
    else if(n==6) cout<<"dcba"<<endl;
    else if(n==7) cout<<"cbaaa"<<endl;
    else if(n==8) cout<<"cbbaa"<<endl;
    else if(n==9) cout<<"dcbaa"<<endl;
    else if(n==10) cout<<"edcba"<<endl;
    else if(n==11) cout<<"cbbaaa"<<endl;
    else if(n==12) cout<<"dcbaaa"<<endl;
    else if(n==13) cout<<"dcbbaa"<<endl;
    else if(n==14) cout<<"edcbaa"<<endl;
    else if(n==15) cout<<"fedcba"<<endl;
    else if(n==16) cout<<"ccbbaaa"<<endl;
    else if(n==17) cout<<"dcbbaaa"<<endl;
    else if(n==18) cout<<"edcbaaa"<<endl;
    else if(n==19) cout<<"edcbbaa"<<endl;
    else if(n==20) cout<<"fedcbaa"<<endl;
	return 0;
} 

---