算法--前缀和

算法基础系列

---

概念

做题思路：暴力枚举 — 算法优化

 前言
 对于一个数组，为了快速求 [L,R]内的和，引入前缀和概念，求静态数组内的和

前缀和：从第一个数 到 当前位置 的 总和

核心思想：空间换时间

普通数组
S₀ = 0
S₁ = a₁;
S_n = a₁ + a₂ + … + a_n;

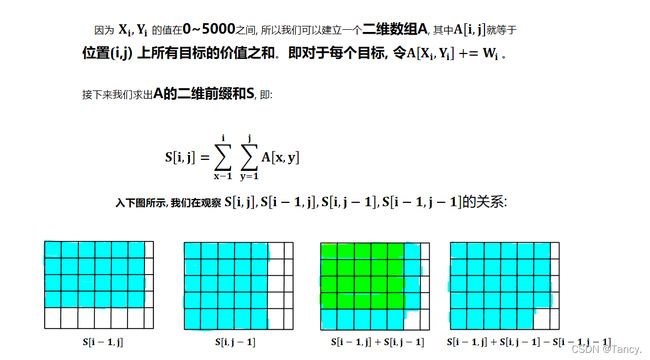
前缀和数组 :开一个数组专门记录前缀和
S_i = S_i-1 + a_i

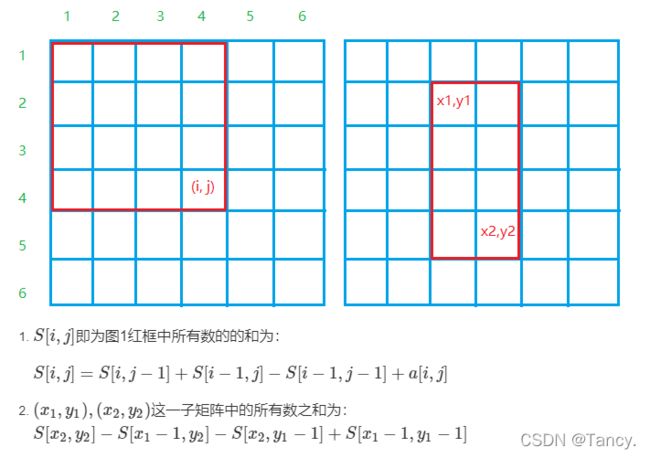
因此，求[L,R]内的和
S_LR = S_R - S_L-1

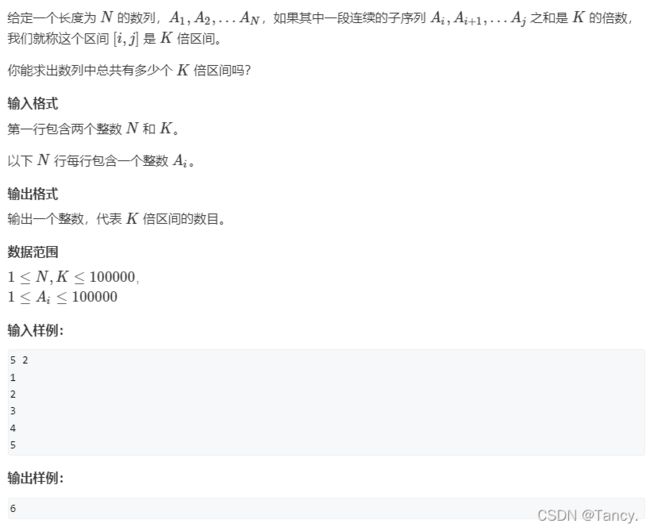
练习题

模板题 795. 前缀和

#include 

using namespace std;

const int N = 1e5 + 10;

int a[N];//正常数组 记录输入的序列
int s[N];// 前缀和数组
int n, m;

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &a[i]);
        s[i] = s[i - 1] + a[i];
    }

    for (int i = 0; i < m; i++)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l - 1]);
    }
    return 0;
}

796. 子矩阵的和

二维的前缀和
利用容斥定理

#include 

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            scanf("%d", &a[i][j]);
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
        }
    while (q--)
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

99. 激光炸弹

思路

#include 
#include 
#include 

using namespace std;

const int N = 5010;

int n, m;
int s[N][N];

int main()
{
    int cnt, R;
    cin >> cnt >> R;
    R = min(5001, R);

    n = m = R;
    while (cnt -- )
    {
        int x, y, w;
        cin >> x >> y >> w;
        x ++, y ++ ;
        n = max(n, x), m = max(m, y);
        s[x][y] += w;
    }

    // 预处理前缀和
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

    int res = 0;

    // 枚举所有边长是R的矩形，枚举(i, j)为右下角
    for (int i = R; i <= n; i ++ )
        for (int j = R; j <= m; j ++ )
            res = max(res, s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R]);

    cout << res << endl;

    return 0;
}

1230. K倍区间

• 思路
  先暴力枚举，发现时间复杂度是n三次方，会TLE

for(int r = 1; r <= n; r ++)
    for(int l = 1; l <= r; l ++)
    {
        int sum = 0;
        for(int i = l; i <= r; i ++)
            sum += a[i];
        if(sum % k == 0) ans ++;
    }

然后用前缀和优化，变为n的平方，还是会超时

for(int i = 1; i <= n; i ++) s[i] = s[i - 1] + a[i]; // 求前缀和

for(int r = 1; r <= n; r ++)
    for(int l = 1; l <= r; l ++)
        if((s[r] - s[l - 1]) % k == 0) ans ++;

用数学方法优化，第二层循环的作用是枚举左端点，
也就是，在 0 到 R-1 内，有多少个 (R - L)%k==0 ，因为 L 在 0 到 R-1内取，所以就是 (R - [0,R-1])%k==0
这个式子的意思就是：在模k的情况下，之前所有点和当前点有都少个相等

代码

#include 

using namespace std;
const int N = 1e5 + 10;
typedef long long LL;//防止爆 int

int n, k;

LL s[N], cnt[N];//cnt 存余数

int main()
{
    scanf("%d%d", &n, &k);

    for (int i = 1; i <= n; i++)
    {
        scanf("%lld", &s[i]);
        s[i] += s[i - 1];//前缀和
    }
    LL res=0; 
    cnt[0] = 1; //第一个余数为1
    for (int i = 1; i <= n; i++)
    {
        res += cnt[s[i] % k];
        cnt[s[i] % k]++;
    }
    printf("%lld\n", res);
    return 0;
}