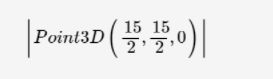在三维空间中表示平面和直线
平面和直线是三维计算机视觉和计算机图形学中有用的几何实体。将它们表示为一组点是低效的,这会导致很大的内存需求,具体取决于用于生成点的步长。
在本文中,我将讨论如何使用向量方程表示平面和直线。我还将介绍如何使用向量形式找到直线和平面之间的交点。
三维线条
我们可以用下面的等式[1]表示向量形式的直线。
p = l₀ + l * ** d,** d ∈ R
其中,I是一个向量,表示直线方向,l₀是直线上的一个点,d是标量。
p是直线上的通用点,这些点定义了线。因此,为了定义直线,我们只需要知道6个数字/参数,就可以用向量形式完整地表示它。
我创建了一个类来表示线向量并绘制它。它由一个vector和一个point_on_line参数化,它们都是3x1 numpy列向量。
要在直线上获得点,我们可以使用该方程。通过缩放vector改变d。
import matplotlib.pyplot as plt
import numpy as np
class Line:
def __init__(self, vector, point_on_line) -> None:
self.vector = np.array(vector).reshape(3, 1)
self.point_on_line = np.array(point_on_line).reshape(3, 1)
def plot(self, step_size=0.1):
points = np.zeros((3, 0))
for i in np.arange(-10, 10, step_size):
points = np.concatenate(
(points, self.point_on_line + i * self.vector), axis=1)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(points[0, :].ravel(),
points[1, :].ravel(),
points[2, :].ravel(),
s=1)
ax.scatter(*self.point_on_line, "r")
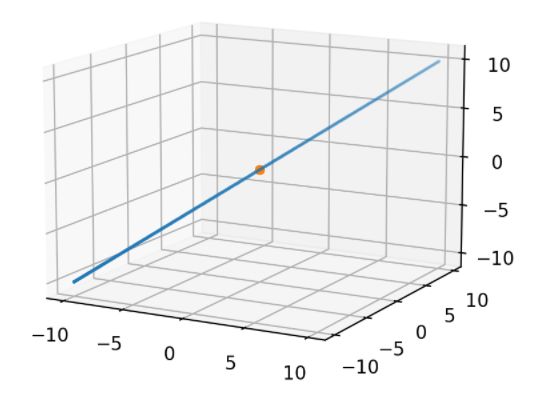
plt.show()我将展示一些样本行。
向量(1,1,1)点(0,0,0);
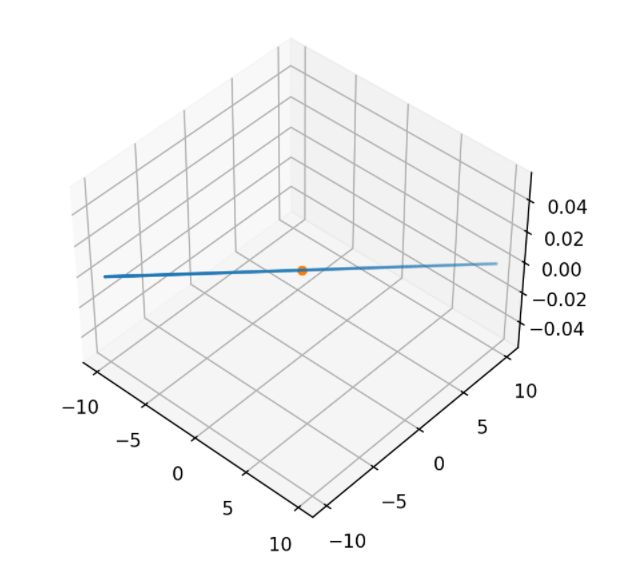
如果你想要一条横跨二维平面的线,那么你可以使用一个在两个坐标中只有非零值的向量,你将在二维平面中得到一条线。
向量(1,1,0)点(0,0,0):
三维平面
我们可以用下面的等式表示向量形式的平面。
(p — p₀) * n = 0,其中n是平面的法向(垂直)向量,p₀是平面上的点。
上述方程式中所有点p的轨迹定义了该平面。(p — **p₀)**表示平面中的向量,n表示平面的正交向量或法向量。因此,对于平面上所有点p的这些向量,相互正交的这两个向量的点积将为零。
用六个数字来表达一个平面十分优雅!
下面是Python中使用上述定义的平面类。
class Plane:
def __init__(self, normal_vector, point_on_plane) -> None:
self.normal_vector = np.array(normal_vector).reshape(3, 1)
self.point_on_plane = np.array(point_on_plane).reshape(3, 1)在本文中,你可以阅读更多表示平面的方法:https://medium.com/@daniel.j.lenton/part-iii-projective-geometry-in-3d-37f36746733b
接下来,让我们看看如何找到直线和平面的交点。
3D中点与平面的交点
现在我们知道了如何在3D中表示点和平面,我们可以看看如何找到这两个几何图形之间的交点。
如果一条直线和某个平面在点p相交,它将同时满足直线和平面方程。因此,为了找到交点,将p的值从直线方程代入平面方程。
(( **l₀ + l * ** d) — p₀) * n = 0
展开这些项可以得到以下等式。
(l * n) d + (l₀ — p₀) * n = 0
求解d得到:
d = (p₀ — l₀) * n / (l * n)
这返回给我们一个点,该点位于直线和平面上。
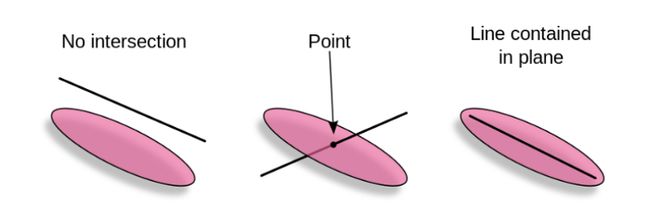
有三种情况。
首先是直线和平面平行,但直线不在平面内。
接下来是,正好有一个交点。
最后,直线平行于平面并在平面中,在这种情况下,直线中的每个点也将位于平面上。因此,在这种情况下,将有无限多个点同时满足这两个方程。
对于前两个案例,l * n = 0,因为对于它们,I垂直于法向量n。否则,我们将得到一个实数d,它可以在直线方程中替换回来,以得到交点:
p = l₀ + l * d
我已经为平面和直线类编写了一个基于上述方程计算交点的函数。请注意,函数是相同的等式,唯一不同的是代码语法。
class Line:
def __init__(self, vector, point_on_line) -> None:
self.vector = np.array(vector).reshape(3, 1)
self.point_on_line = np.array(point_on_line).reshape(3, 1)
def intersect(self, plane):
if plane.normal_vector.ravel().dot(self.vector.ravel()) != 0:
d = (plane.point_on_plane - self.point_on_line).ravel().dot(
plane.normal_vector.ravel()) / plane.normal_vector.ravel().dot(
self.vector.ravel())
return self.point_on_line + (d * self.vector)
return Noneclass Plane:
def __init__(self, normal_vector, point_on_plane) -> None:
self.normal_vector = np.array(normal_vector).reshape(3, 1)
self.point_on_plane = np.array(point_on_plane).reshape(3, 1)
def intersect(self, line: Line):
if self.normal_vector.ravel().dot(line.vector.ravel()) != 0:
d = (self.point_on_plane - line.point_on_line).ravel().dot(
self.normal_vector.ravel()) / self.normal_vector.ravel().dot(
line.vector.ravel())
return line.point_on_line + (d * line.vector)
return None现在,我们可以使用plane和line类来查找它们之间的交点。
例如:
l1 = Line((1, 1, 0), (0, 0, 0))
p1 = Plane((1, 1, 1), (5, 5, 5))
print(p1.intersect(l1))
# Output
#[[7.5]
# [7.5]
# [0. ]]我们可以使用Symphy验证结果:
from sympy.geometry import Line, Segment
from sympy import Point, Eq
l1 = Line(Point(0,0,0), Point(1,1,0))
from sympy import Plane, Point3D
p1 = Plane((5,5,5), normal_vector=(1,1,1))
print(p1.intersection(l1))我们也使用Symphy实现来验证我们的代码。
结论
在本文中,我们研究了3D中的线和平面。我们看到了它们的向量方程,以及如何用一个向量和一个点来表示它们。
这是一个非常紧凑的表示,只有六个数字。我们最终了解了如何找到两者之间的交叉点,并查看了三种可能的交叉点情况。
参考文献
[1] https://en.wikipedia.org/wiki/Line%E2%80%93plane_intersection
☆ END ☆
如果看到这里,说明你喜欢这篇文章,请转发、点赞。微信搜索「uncle_pn」,欢迎添加小编微信「 woshicver」,每日朋友圈更新一篇高质量博文。
↓扫描二维码添加小编↓