“函数”是高中课本就有的概念,“关系”是大学离散数学里研究集合元素的联系时出现的更常见的概念。上课的时候其实大部分内容没有难度,给人“废话”的感觉,但是还是有些东西超出了高中的认知,还有些与程序设计结合起来后认识更深了。
什么是关系
关系(relation):有集合\(A,B\),那么\(A\times B\)(直积)的任意子集都是一个\(A\to B\)的关系。关系相当于一个可以一对多的函数,每个A中元素可对应B中多个元素,每个B中元素可以对应A中任意元素。任取A中一个元素x和B中一个元素y,x和y要么是“有关系”,要么是“没有关系”。用\(xRy\)表示存在关系\(\langle x,y\rangle\)也可以选择用谓词\(f(x,y)\)表示x和y是否有关系,有则为真,无则为假。
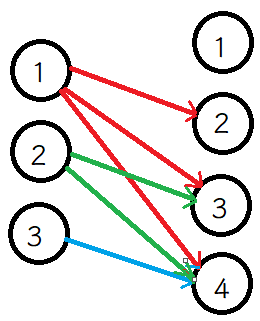
关系可以用“连线图”来表示,也可以用矩阵来表示,比如\(\{1,2,3\}\to\{1,2,3,4\}\)上的小于关系:
关系的逆很好理解,将箭头倒转就可以,关系的复合就是在右侧加上第二列连线到第三列,那么能从第一列连到第三列的所有元素对就是复合关系,这与函数的理论是基本一致的。
自反,对称与传递
对于一个自身上的映射(即\(A\times A\)上),几个耳熟但不能详的名词:
- 自反(reflexive):任意\(x\in A\)都有\(xRx\),那么A就是自反关系,即每个元素都有到自己的关系。
- 非自反(inreflexive):任意\(x\in A\)都有\(x/ \hspace{-0.6em}Rx\),那么A就是非自反关系,即每个元素都不存在到自己的关系。显然集合只能是自反,非自反,和两者都不是中的一种。
- 对称(symmetric):任意\(xRy\),则必有\(yRx\),那么A就是对称关系,对称关系也可以用“逆关系等于自身”来描述。
- 反对称(antisymmetric):任意\(xRy\),若有\(yRx\),则必有\(x=y\),即不存在两个不同元素有互相的对称关系。但是可以指向自身,因此有些关系可以既对称又反对称。
- 传递(transitive):任意\(xRy\)和\(yRz\),则必有\(xRz\),那么A就是传递关系,传递关系也可以用\(R^2\subseteq R\)来表述(\(R^2\)表示R与R的复合\(R\cdot R\))。
构造关系闭包
关系闭包提出的问题是:给定任意关系\(R\),并在\(R\)基础上添加最少的关系,如何把\(R\)变成具有给定性质的关系?
创建一个自反闭包很简单,把所有\(xRx\)加上就可以;创建对称闭包也很简单,对于每个\(xRy\),如果\(yRx\)不存在,加上就可以。
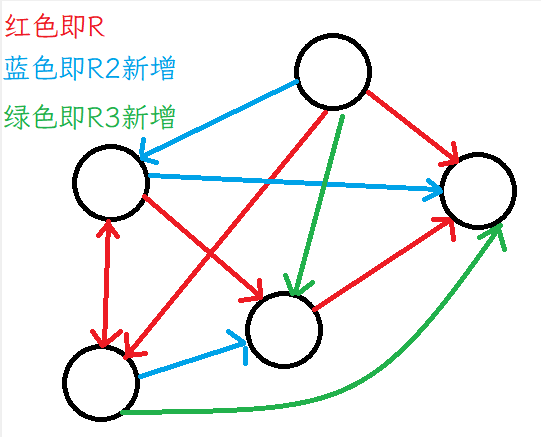
那么传递闭包呢?传递闭包的结论是:构造\(R_t=R\cup R^2 \cup R^3\cup...\),得到的\(R_t\)即为包含R的传递闭包关系。
证明两边相等:先证右属于左,用归纳法证明,右侧\(R^1\subseteq R_t\)显然;假设\(R^n\subseteq R_t\),那么任意\(\langle x,y\rangle\in R^{n+1}=R^n\cdot R\),都应该存在\(z\)使\(\langle x,z\rangle\in R\wedge \langle z,y\rangle\in R^n\),而\(R,R^n\subseteq R_t\),所以\(\langle x,z\rangle,\langle z,y\rangle\)都是\(R_t\)的元素,由传递集合性质\(\langle x,y\rangle\in R_t\)。
再证左属于右,任意\(R\cup R^2 \cup R^3\cup...\)中的元素一定在某一个\(R^i\)中,设有\(\langle x,z\rangle\in R_s\),\(\langle z,y\rangle\in R_t\),显然有\(\langle x,y\rangle\in R_{s+t}\)也在集合中,因此\(R\cup R^2 \cup R^3\cup...\)就是传递的,它比最小闭包\(R_t\)大或相等。因此等式成立。
这个结论是正确的,同时也是可计算的,含有n个元素的集合,最多有\(2^{n^2}\)种可能的关系,所以右边的集合一定会出现重复,数量是有限的。
传递关系与Warshell算法
传递关系要求\(f((x,y)\wedge f(y,z))\to f(x,z)\)。\(R\)相当于x直接走到z,\(R^2\)相当于x走两步到z,以此类推,只要最终x能走到z,就有\(f(x,z)=1\),我们用下面的流程计算\(R\cup R^2 \cup R^3\cup...\)(假设有n个元素):
- 令\(k = 1\)
- 枚举所有\(\langle i,j\rangle\in n\times n\),若\(f_{k-1}(i,k)\wedge f_{k-1}(k,j)\),则令\(f_k(i,j)=1\)。(这里的\(f_k\)指不超过k步能走到)
- 递增k,重复运算到k大于n。
每一次k取A的枚举解出\(R\cup...R^A\),代表求解i能否在A步以内走到j,由于A步以下的答案都已经求解,若i能在A-1步内走到k,k能在A-1步内走到j,那么i就可以走到j。复杂度为\(O(n^3)\)。
刚刚一直在用“走到”来描述一次关系变换,其实这个问题是可以抽象为一个图论问题的,关系就是一张有向图,每个图能走到的所有点全部加起来就是传递闭包。在实际编程中,上述算法的第一维可以省略,这样就变成了Floyed算法。
//Floyed
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
f[i][j] = f[i][k] | f[k][j];
等价,偏序与拟序
介绍了自反,对称与传递,下面得说说他们存在的意义了。
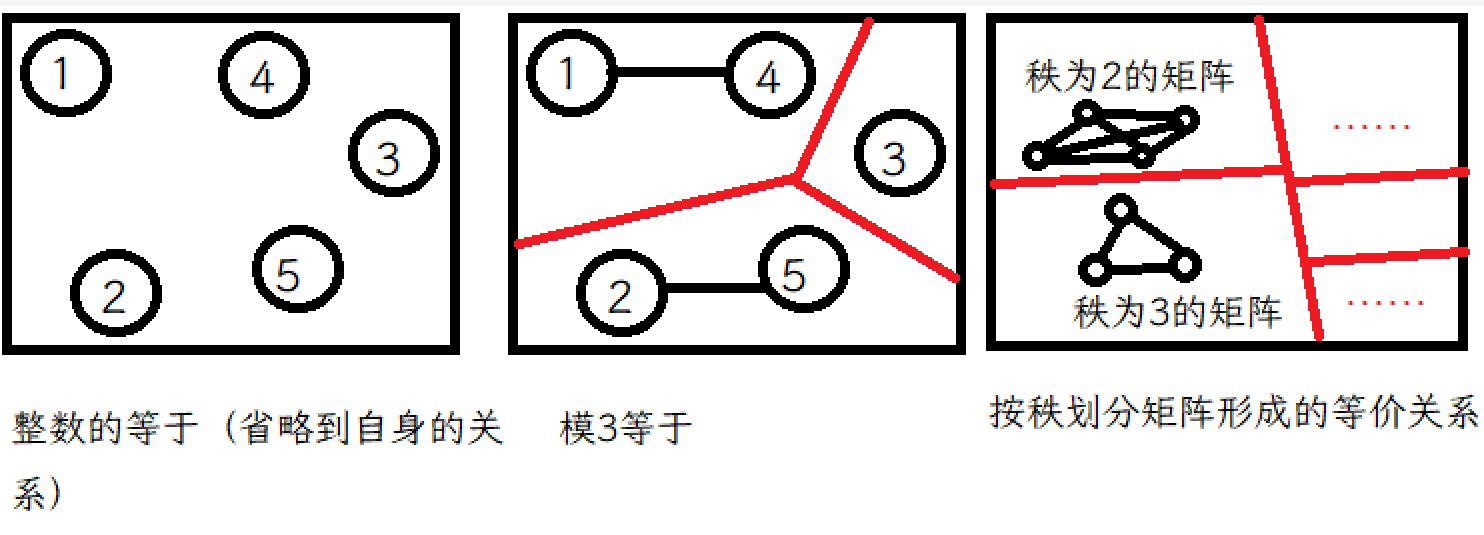
等价关系(equivelance):满足自反,对称,传递的关系即为等价关系。自然数的“等于”是典型的等价关系。假设有集合\(\{1,2,3,4,5,6,7,8\}\),显然只有\(eq(x,x)=1, eq(x,y)=0\)每个元素只和自己相等。“模3等于”也是等价关系,此时模3得1的数互相关系,模3得2的数互相关系,模3得0的数互相关系,他们之间却都没有关系。
容易发现,等价关系将集合中的元素进行了“分组”,组内是全联通的,任意两元素都等价,而组间都没有关系,数的等于是等价关系,矩阵的相似等一样是等价关系,都是按照性质分类带来的结果。
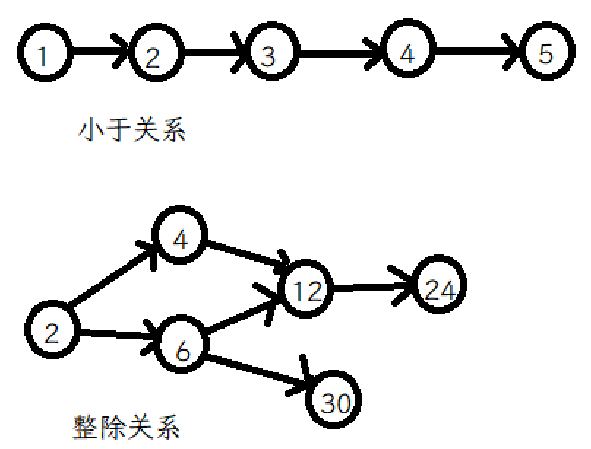
偏序关系(partial order):满足自反,反对称,传递的关系即为偏序关系,自然数的“小于等于”是典型的偏序关系,整数的整除关系也是典型的偏序关系。
拟序关系(quasi order):满足非自反和传递的关系即为拟序关系(显然是反对称的),“小于”是典型的拟序关系。
偏序和拟序的差别在于有无自反。省略到自己的关系,在偏序或拟序关系下,由于反对称性,元素会形成一张有向无环图。对于“小于”来说,所有元素形成了一条链,这就是排序的基础。
关系的规则与程序设计
“自然数的等于”是等价关系的典型,“自然数的小于”是拟序关系的典型。这样的规则一方面便于我们记忆,另一方面解释了这些关系的本质。
而第三个方面,我们要确保使用小于和等于时满足这些性质。比如在C++里,使用map和set需要支持==号,使用sort需要一个小于号,如果你重载了自定义类型的比较运算符号,就一定要确保它满足对应的性质。比如重载小于号的时候,一定要保证重载出的符号满足非自反性和传递性,只有这样才能把全体元素连成一条链,按链上的大小规则排序,否则(比如使用了小于等于号导致自反)将不能正确排序。
典型例题:洛谷 P2123 皇后游戏