一般线性回归---完整过程
##线性回归包括几个方面:数据观察,初步拟合,交互作用,多重共线性,回归诊断,拟合中出现的离群点,杠杆值,强影响点,删除后,重新拟合,模型比较--之后可能要预测,因此需要数据交叉验证分成2部分,一部分拟合,一部分验证。
数据为state.x77数据集---本次利用ols 最小二乘法=最小平方法直线回归拟合分析
###线性回归
##线性回归包括几个方面:数据观察,初步拟合,交互作用,多重共线性,回归诊断,拟合中出现的离群点,杠杆值,强影响点,删除后,重新拟合,模型比较--
##之后可能要预测,因此需要数据交叉验证分成2部分,一部分拟合,一部分验证。
rm(list = ls())
gc()
library(car)
###本次利用ols 最小二乘法=最小平方法直线回归拟合分析---数据来自于state.x77数据集
state.x77
data<-state.x77
data<-as.data.frame(data) ###lm一定要data.frame格式
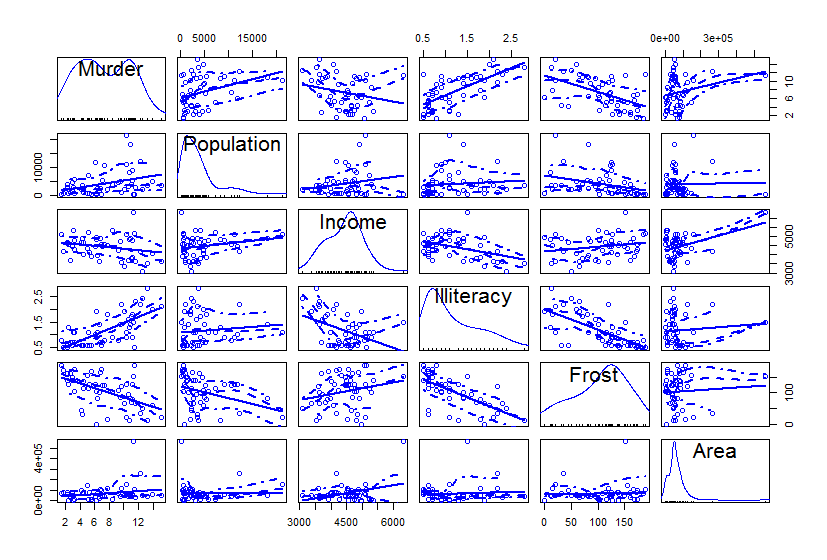
###先看看数据特点 car包的scatterplotMatrix()
data1<-data[,c("Murder","Population","Income","Illiteracy","Frost","Area")]
scatterplotMatrix(data1)
###线性拟合
fit<-lm(formula = Murder ~ Population +Income+Illiteracy+Frost +Area, data = data)
###多重共线性:sqrt(vif(fit))>2那一列 删去
sqrt(vif(fit))
summary(fit) ###Population Illiteracy 具有与murder的线性关系
###看看之间是不是具有交互项
summary(lm(Murder~Population+Illiteracy+Population:Illiteracy,data=data)) ###没有交互项
summary(lm(Murder~Population+Illiteracy,data=data)) ##公式为:Murder=1.652e+00+2.242e-04*Population+4.081e+00*Illiteracy
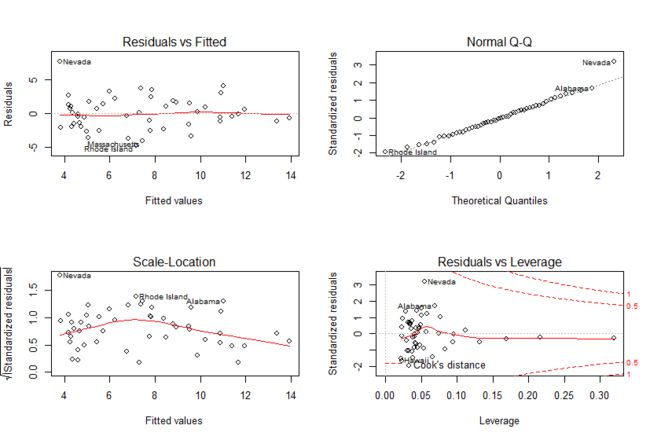
###残差-回归诊断 线性 正态性 独立性 方差齐性
op<-par(mfrow=c(2,2))
plot(lm(Murder~Population+Illiteracy,data=data)) ## 没有强影响点(没有大的cook值),Nevada>2(y值)为离群点,删去离群点
par(op)
###删去Nevada 重新拟合
rownames(data)
data2<-data[rownames(data)!="Nevada",]
summary(lm(Murder~Population+Illiteracy,data=data2))
op<-par(mfrow=c(2,2))
plot(lm(Murder~Population+Illiteracy,data=data2)) ## 没有强影响点(没有大的cook值),Nevada>2(y值)为离群点,删去离群点
par(op)
###改进的残差分析
class(data2)
str(data2)
fit_1<-lm(Murder~Population+Illiteracy,data=data2)
qqPlot(fit_1,id.method="identify",labels=row.names(data2)) ###qqplot正态性检验
durbinWatsonTest(fit_1) ##独立性 durbin-watson检验 p>0.05,残差独立
crPlots(fit_1) ###线性
ncvTest(fit_1) ###方差齐性 p>0.05
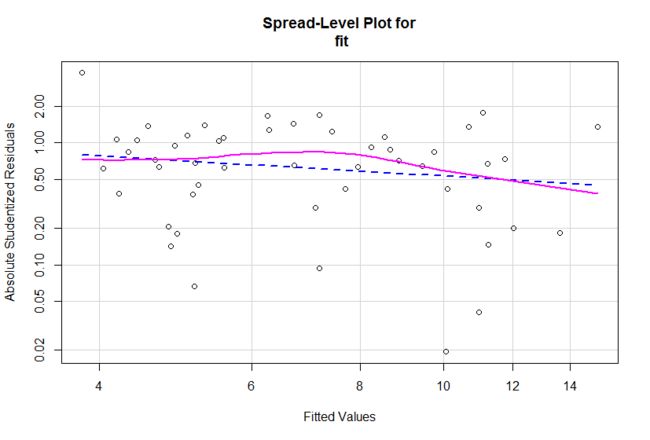
spreadLevelPlot(fit) ###方差齐性作图 水平随机分布的直线
###异常观察值检测 -总和方法
influencePlot(fit_1,id.method="identify")
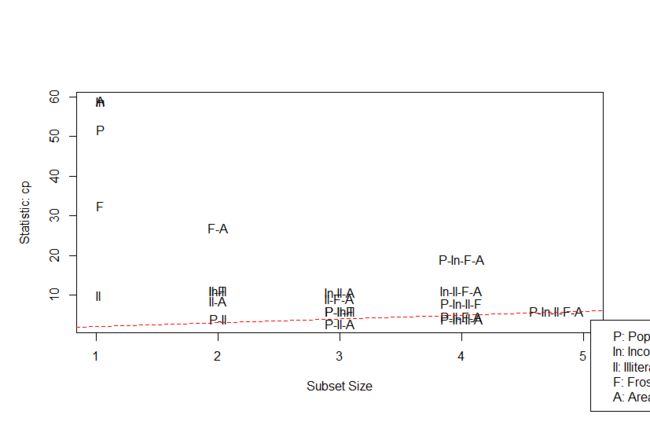
###最佳回归模型确定--全子集回归
library(leaps)
leaps<-regsubsets(Murder ~ Population +Income+Illiteracy+Frost +Area, data = data,nbest = 5)
plot(leaps,scale="adjr2") ##最好是2个自变量x
library(car)
subsets(leaps,statistic = "cp")
abline(1,1,lty=2,col="red")
###以上分析只是为了在数据基础上建模和解释参加模拟的数据;如果要模拟的曲线用来预测将要出来的数据时怎么办?-深度分析之交叉验证
##交叉验证--9成数据来模拟,1成数据来验证
##set.seed()保证操作的可重复性,别人也用1234,产生的随机数就和你的一样了
set.seed(1234)
##选取训练集--从nrow(df)中即699个数字中,无放回(如果放回,replace=T)抽取0.7*nrow(df)个数字
train<-sample(nrow(data),0.7*nrow(data))
##提取出训练集的列表
df.train<-data[train,]
###提取验证集的列表
df.validate<-data[-train,]
##看看各个列表的数目
table(df.train$Murder)
table(df.validate$Murder)
##拟合:
fit_logit<-lm(Murder~.,data = df.train,family = binomial())
summary(fit_logit)
##用模拟的数据在新的数据集中,进行数据的验证: type = "response" 直接返回预测的概率值0~1之间
prob<-predict(fit_logit,df.validate,type="response")
prob
#3将概率大于0.5的定义为恶性肿瘤;概率小于0.5的定义为良性肿瘤,
logit.pred<-factor(prob>.5,levels = c(FALSE,TRUE),labels = c("benign","malignant"))
logit.pred
##3得出实际与预测的交叉表
logit.perf<-table(df.validate$class,logit.pred,dnn=c("Actual","Predicted"))
###预测出118个良,76个恶性
#### 准确率为(76+118)/(129+81)=0.92 (76+118)/200=0.97
(76+118)/(129+81) ###有问题
(76+118)/200
###再回归来看 有几个模拟概率>0.05,不满足,可以删除再模拟,也可以用下面的方法
logit.fit.reduced<-step(fit_logit)
###哪个x值贡献最大呢?scale先规范化为均值为1,方差为0的数据集
data_3<-scale(data) #scale数据
data_3<-as.data.frame(data_3)
coef(lm(formula = Murder ~ Population +Income+Illiteracy+Frost +Area, data = data_3))
数据如下:
A B
25 7
25 9
25 9
27 12
27 14
27 16
24 16
30 14
30 16
31 16
30 17
31 19
30 21
28 24
32 15
32 16
32 17
32 25
34 27
34 15
34 15
35 15
35 16
34 19
35 18
36 17
37 18
38 20
40 22
39 25
43 24
setwd("c:/Users/xx/Desktop/Homework_4A/")
> data<-read.table(file ="data_1.txt",header=T,sep = "\t")
> ##散点图
> attach(data)
The following objects are masked from data (pos = 5):
A, B
The following objects are masked from data (pos = 6):
A, B
The following objects are masked from data (pos = 8):
A, B
> ###pearson线性相关关系分析
> cor.test(data$A,data$B)
Pearson's product-moment correlation
data: data$A and data$B
t = 4.1427, df = 29, p-value = 0.0002712
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.3257757 0.7927878
sample estimates:
cor
0.6097313
> pic<-lm(B~A,data = data)
> print(pic)
Call:
lm(formula = B ~ A, data = data)
Coefficients:
(Intercept) A
-2.3350 0.6113
> summary(pic)
Call:
lm(formula = B ~ A, data = data)
Residuals:
Min 1Q Median 3Q Max
-5.9469 -2.4765 -0.6145 1.4137 9.2193
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.3350 4.7717 -0.489 0.628274
A 0.6113 0.1476 4.143 0.000271 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.831 on 29 degrees of freedom
Multiple R-squared: 0.3718, Adjusted R-squared: 0.3501
F-statistic: 17.16 on 1 and 29 DF, p-value: 0.0002712
> #拟合直线
> plot(B~A,data=data)
> abline(pic)
> anova(pic)
Analysis of Variance Table
Response: B
Df Sum Sq Mean Sq F value Pr(>F)
A 1 251.85 251.846 17.162 0.0002712 ***
Residuals 29 425.57 14.675
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> ##拟合直线诊断-残差分析:标准方法
> op<-par(mfrow=c(2,2))
> plot(pic)
> par(op)
> ###改进的回归拟合诊断方法:
> ##正态性检验
> qqPlot(pic,id.method="identify",simlabels=row.names(data),ulate=TRUE,main="Normal Q-Q Plot")
[1] 14 19
> ###残差独立性检验 p>0.05,独立
> library(car)
> durbinWatsonTest(pic)
lag Autocorrelation D-W Statistic p-value
1 0.4027404 1.111413 0.008
Alternative hypothesis: rho != 0
> ##残差线性
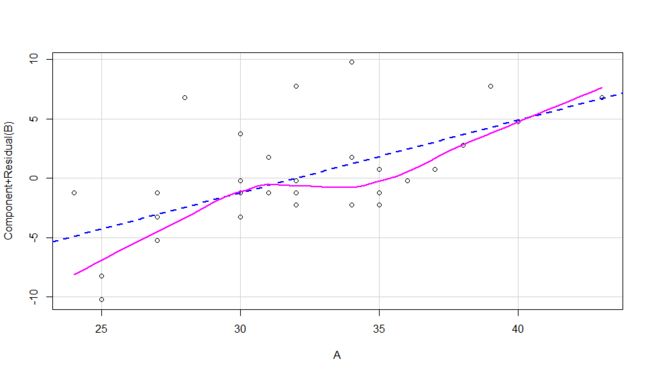
> crPlots(pic)
> ##同方差性 >0.05,满足方差不变
> ncvTest(pic)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 1.413038, Df = 1, p = 0.23455
> spreadLevelPlot(pic)
Suggested power transformation: 3.43003
> ##离群值
> outlierTest(pic)
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
14 2.741071 0.010545 0.3269
> ##强影响点
> avPlots(pic)
> ####将离散点、杠杆值、强影响点做到一个图中 纵坐标绝对值大于2为离群点;水平大于0.2或者0.3的是高杠杆值;
> #圆圈大小与影响成正比
> influencePlot(pic,main="Influence Plot",sub="Circle size is proportional to Cook`s distance")
StudRes Hat CookD
1 -1.69284861 0.10495836 1.578707e-01
7 1.02479319 0.12721355 7.640411e-02
14 2.74107120 0.05599694 1.819728e-01
19 2.46795140 0.03819278 1.028721e-01
31 0.01449139 0.21178329 2.921952e-05
> ## 验证 可信度
> anova(pic)
Analysis of Variance Table
Response: B
Df Sum Sq Mean Sq F value Pr(>F)
A 1 251.85 251.846 17.162 0.0002712 ***
Residuals 29 425.57 14.675
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#广义线性模型-logistic 与泊松回归 Y值类型为0/1或者一些计数型的
#logistics-AER包,婚外情数据affairs,各种因素是不是跟婚外情有关系
data(Affairs,package = "AER")
#变量x的统计分析
summary(Affairs)
#相应变量y的统计数值
table(Affairs$affairs)
#这时候我们需要把婚外情变化成二值型数据0/1 只关心有没有 ynaffair可以任意取名字,新增的一列而已
Affairs$ynaffair[Affairs$affairs>0]<-1
Affairs$ynaffair[Affairs$affairs==0]<-0
Affairs$ynaffair<-factor(Affairs$ynaffair,levels = c(0,1),labels = c("No","Yes"))
table(Affairs$ynaffair)
##此时因为Y变为二值型变量0/1,可以用logistic回归了
fit<-glm(ynaffair~gender+age+yearsmarried+children+religiousness+education+occupation+rating,data=Affairs,family=binomial())
summary(fit)
#去除拟合不好的再拟合
fit_reduced<-glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family=binomial())
summary(fit_reduced)
##因为fit_reduced拟合是fit拟合的子集,可以用卡方检验的anova进行比较 p>0.05,没有差别,因此可以删去无关的数据
anova(fit_reduced,fit,test = "Chisq")
##可以用coef单独看看系数
coef(fit_reduced)
##方法一:用优势比解释系数
##因为响应变量是Y=1的log值,不好解释,可以e-指数化后恢复原来的值;保持年龄什么的不变,婚龄增加一年,婚外情
##优势比乘于1.106.。。因此大于1,上升,小于1下降优势比 若分析几年,就乘于几年就好了*n --n年
exp(coef(fit_reduced))
##系数置信区间
confint(fit_reduced)
##指数化的结果--一般用这个
exp(confint(fit_reduced))
##方法二:用概率解释系数
##创建感兴趣的数据集
testdata<-data.frame(rating=c(1,2,3,4,5),age=mean(Affairs$age),yearsmarried=mean(Affairs$yearsmarried),
religiousness=mean(Affairs$religiousness))
testdata
testdata$prob<-predict(fit_reduced,newdata = testdata,type = "response")
testdata
##过度离势的判断,避免不准确的显著性检验
fit_reduced<-glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family=binomial())
fit.od<-glm(ynaffair~age+yearsmarried+religiousness+rating,data=Affairs,family = quasibinomial())
#检验 >0.34,没有过度离势,之前的检验显著可信;
pchisq(summary(fit.od)$dispersion*fit_reduced$df.residual,fit_reduced$df.residual,lower=F)
##常见的回归诊断可以用线性回归诊断也可以用下面的
##一般方法:
op<-par(mfrow=c(2,2))
plot(fit_reduced)
par(op)
###本章的方法 预测值与残差值
plot(predict(fit_reduced,type = "response"),residuals(fit_reduced,type="deviance"))
###异常值--hat value 学生化残差,cook距离
plot(hatvalues(fit_reduced))
plot(rstudent(fit_reduced))
plot(cooks.distance(fit_reduced))
###泊松回归分析---robust包
library(robust)
data(breslow.dat,package = "robust")
names(breslow.dat)
summary(breslow.dat[c(6,7,8,10)])
##基本图形描述
op<-par(no.readonly = T)
par(mfrow=c(1,2))
attach(breslow.dat)
hist(sumY,breaks = 20,xlab = "Seizure Count",main = "Distribution of Seizures")
boxplot(sumY~Trt,xlab="Treatment",main="Group Comparisons")
par(op)
###回归拟合:
fit_BS<-glm(sumY~Base+Age+Trt,family = poisson(),data=breslow.dat)
summary(fit_BS)
###系数分析
coef(fit_BS)
##指数化
exp(coef(fit_BS))
##过度离势分析
##残差偏差与残差自由度比值 远远大于1 说明过度离势
deviance(fit_BS)/df.residual(fit_BS)
#或用qcc包中进行过度离势分析 p<0.05 进一步说明过度离势
library(qcc)
qcc.overdispersion.test(breslow.dat$sumY,type="poisson")
##将poisson换成quasipoisson 重新拟合
fit<-glm(sumY~Base+Age+Trt,family = quasipoisson(),data=breslow.dat)
summary(fit)
##########################################################
##第五题 回归分析
data_5<-read.table("final5/diabetes.txt",header = T,sep = "\t")
data_5<-as.data.frame(data_5)
boxplot(data_5)
library(car)
scatterplotMatrix(data_5,spread=F,main="Scatter Plot Matrix")
##拟合
fit_5<-lm(Y~X1+X2+X3+X4,data = data_5)
summary(fit_5)
#回归诊断--标准方法
op<-par(mfrow=c(2,2))
plot(fit_5)
par(op)
par(par(mfrow=c(2,2)))
##离群点
outlierTest(fit_5)
##逐步回归分析 P大于0.05可以删去x1 x2
fit_5_new<-lm(Y~X3+X4,data = data_5)
anova(fit_5,fit_5_new)
##交互作用
fit_5_ab<-lm(Y~X3+X4+X3:X4,data = data_5)
fit_5_ab
##交互结果展示
library(effects)
plot(effect("X3:X4",fit_5_ab),multiline=T)
##线性回归包括几个方面:数据观察,初步拟合,交互作用,多重共线性,回归诊断,拟合中出现的离群点,杠杆值,强影响点,删除后,重新拟合,模型比较--
##之后可能要预测,因此需要数据交叉验证分成2部分,一部分拟合,一部分验证。