推荐系统(七)xDeepFM模型
推荐系统(七)xDeepFM模型
推荐系统系列博客:
- 推荐系统(一)推荐系统整体概览
- 推荐系统(二)GBDT+LR模型
- 推荐系统(三)Factorization Machines(FM)
- 推荐系统(四)Field-aware Factorization Machines(FFM)
- 推荐系统(五)wide&deep
- 推荐系统(六)Deep & Cross Network(DCN)
这篇文章是中科大、北邮和微软合作发表在KDD’18上的文章,从论文写作手法上来看充满了浓浓的学院风。言归正传,乍一看论文标题xDeepFM还以为是对DeepFM的改进,实际上不是,xDeepFM是对上一篇博客中介绍的DCN(deep&cross network)的改进,这也是为什么这篇博客会介绍xDeepFM的原因。本篇博客将会从一下几个方面来介绍xDeepFM:
- 论文动机
- xDeepFM模型整体结构
- xDeepFM中CIN网络结构
- 联合训练目标函数
- 总结
一、论文动机
这篇文章diss的一个重点就是DCN网络中cross network部分,因此,个人强烈建议在看xDeepFM之前,请先移步去本人的上一篇博客看看DCN。我们先来看看xDeepFM给出的论据:
- 这篇文章认为DCN网络中cross部分只是对 x 0 x_0 x0(输入向量)某种特殊的放缩(交叉)。
- 这篇文章认为DCN网络中cross部分的交叉是bit-wise的而不是像鼻祖FM那样是vector-wise的。这里简单描述bit-wise和vector-wise的区别,假设有两个特征 A , B A,B A,B,embedding维度为4,所以 A ( a 1 , a 2 , a 3 , a 4 ) A(a_1,a_2,a_3,a_4) A(a1,a2,a3,a4), B ( b 1 , b 2 , b 3 , b 4 ) B(b_1,b_2,b_3,b_4) B(b1,b2,b3,b4),那么bit-wise的交互则为 ( w a , b a 1 b 1 , w a , b a 2 b 2 , w a , b a 3 b 3 , w a , b a 4 b 4 ) (w_{a,b}a_1b_1,w_{a,b}a_2b_2,w_{a,b}a_3b_3,w_{a,b}a_4b_4) (wa,ba1b1,wa,ba2b2,wa,ba3b3,wa,ba4b4),而vector-wise交互则为 w a , b ( a 1 b 1 , a 2 b 2 , a 3 b 3 , a 4 b 4 ) w_{a,b}(a_1b_1,a_2b_2,a_3b_3,a_4b_4) wa,b(a1b1,a2b2,a3b3,a4b4)。通俗说bit-wise交互的粒度为每个特征embedding向量的每个bit上,而vector-wise交互粒度为特征与特征之间。
上面两个点,第二个点没啥好说的,重点来看看第一个点。xDeepFM这篇文章中给出了公式证明,先来看看DCN中cross部分的交叉公式:
x k = x 0 x k − 1 T w k + b k + x k − 1 (1) x_k = x_0x^T_{k-1}w_k + b_k + x_{k-1} \tag{1} xk=x0xk−1Twk+bk+xk−1(1)
再来看看xDeepFM中的证明:
x 1 = x 0 ( x 0 T w 1 ) + x 0 = x 0 ( x 0 T w 1 + 1 ) = α 1 x 0 (2) \begin{aligned} x_1 &= x_0(x_0^Tw_1) + x_0 \\ &= x_0(x_0^Tw_1 + 1) \\ &=\alpha^1x_0 \tag{2} \end{aligned} x1=x0(x0Tw1)+x0=x0(x0Tw1+1)=α1x0(2)
其中, α 1 = x 0 T w 1 + 1 \alpha^1=x_0^Tw_1 + 1 α1=x0Tw1+1。
以此类推,
x i + 1 = α i + 1 x 0 = α i ( x 0 T w i + 1 + 1 ) x 0 = α i − 1 ( x 0 T w i + 1 ) ( x 0 T w i + 1 + 1 ) x 0 = α i − 2 ( x 0 T w i − 1 + 1 ) ( x 0 T w i + 1 ) ( x 0 T w i + 1 + 1 ) x 0 = . . . = ( x 0 T w 1 + 1 ) . . . ( x 0 T w i − 1 + 1 ) ( x 0 T w i + 1 ) ( x 0 T w i + 1 + 1 ) x 0 (3) \begin{aligned} x_{i+1} &= \alpha^{i+1}x_0 \\ &= \alpha^{i}(x_0^Tw_{i+1} + 1)x_0 \\ &= \alpha^{i-1}(x_0^Tw_{i} + 1)(x_0^Tw_{i+1} + 1)x_0 \\ &= \alpha^{i-2}(x_0^Tw_{i-1} + 1)(x_0^Tw_{i} + 1)(x_0^Tw_{i+1} + 1)x_0 \\ &=... \\ &= (x_0^Tw_1 + 1)...(x_0^Tw_{i-1} + 1)(x_0^Tw_{i} + 1)(x_0^Tw_{i+1}+ 1)x_0 \tag{3} \end{aligned} xi+1=αi+1x0=αi(x0Twi+1+1)x0=αi−1(x0Twi+1)(x0Twi+1+1)x0=αi−2(x0Twi−1+1)(x0Twi+1)(x0Twi+1+1)x0=...=(x0Tw1+1)...(x0Twi−1+1)(x0Twi+1)(x0Twi+1+1)x0(3)
xDeepFM认为这种交叉是一种对 x 0 x_0 x0特殊的交叉,但其实吧,我个人认为DCN中这种交叉是没什么问题的,直接拿我在DCN(deep&cross network)这篇博客里的例子来看:
假设样本只有两个特征,为了简单,假设每个特征的embedding维度为1,偏置 b b b直接忽略,设 x 0 = [ x 0 , 1 x 0 , 2 ] x_0=\begin{bmatrix} x_{0,1} \\ x_{0,2} \\ \end{bmatrix} x0=[x0,1x0,2],那么,则有:
x 1 = x 0 ⊙ ( w 1 x 1 ) + x 0 = [ x 0 , 1 x 0 , 2 ] ⊙ [ w 1 , 1 x 0 , 1 + w 1 , 2 x 0 , 2 w 1 , 1 x 0 , 1 + w 1 , 2 x 0 , 2 ] + [ x 0 , 1 x 0 , 2 ] = [ x 0 , 1 ( w 1 , 1 x 0 , 1 + w 1 , 2 x 0 , 2 ) + x 0 , 1 x 0 , 2 ( w 1 , 1 x 0 , 1 + w 1 , 2 x 0 , 2 ) + x 0 , 2 ] = [ w 1 , 1 x 0 , 1 2 + w 1 , 2 x 0 , 2 x 0 , 1 + x 0 , 1 w 1 , 1 x 0 , 1 x 0 , 2 + w 1 , 2 x 0 , 2 2 + x 0 , 2 ] (4) \begin{aligned} x_1&=x_0\odot(w_1x_1) + x_0 \\ &=\begin{bmatrix} x_{0,1} \\ x_{0,2} \\ \end{bmatrix}\odot\begin{bmatrix} w_{1,1}x_{0,1} +w_{1,2}x_{0,2} \\ w_{1,1}x_{0,1} +w_{1,2}x_{0,2} \\ \end{bmatrix} + \begin{bmatrix} x_{0,1} \\ x_{0,2} \\ \end{bmatrix} \\\\ &=\begin{bmatrix} x_{0,1}(w_{1,1}x_{0,1} +w_{1,2}x_{0,2}) + x_{0,1} \\ x_{0,2}(w_{1,1}x_{0,1} +w_{1,2}x_{0,2}) + x_{0,2}\\ \end{bmatrix} \\\\ &=\begin{bmatrix} w_{1,1}x_{0,1}^2 +w_{1,2}x_{0,2}x_{0,1} + x_{0,1} \\ w_{1,1}x_{0,1} x_{0,2} +w_{1,2}x_{0,2}^2 + x_{0,2}\\ \end{bmatrix} \end{aligned} \tag{4} x1=x0⊙(w1x1)+x0=[x0,1x0,2]⊙[w1,1x0,1+w1,2x0,2w1,1x0,1+w1,2x0,2]+[x0,1x0,2]=[x0,1(w1,1x0,1+w1,2x0,2)+x0,1x0,2(w1,1x0,1+w1,2x0,2)+x0,2]=[w1,1x0,12+w1,2x0,2x0,1+x0,1w1,1x0,1x0,2+w1,2x0,22+x0,2](4)
从上面的例子能够看出,DCN中cross部分交叉项包含了 x 0 , 1 2 , x 0 , 2 x 0 , 1 , . . . x_{0,1}^2,x_{0,2}x_{0,1},... x0,12,x0,2x0,1,...等交叉项,所以DCN中这种cross的设计是没什么问题的。所以xDeepFM是否在真实的场景中效果比DCN好,这一点我是持怀疑态度的,但有一点可以肯定的是xDeepFM网络结构相对复杂,参数量相对大的多,计算复杂度高,在工业界大规模数据场景下,能否顺利落地是个问题。
二、xDeepFM模型整体结构
关于xDeepFM的整天网络结构,如下图所示(图片直接摘自原论文):

从上图可以看出,xDeepFM依然延续了wide&deep,DCN这种混合网络结构模式,左手画个xxx网络用于构造高阶交叉特征,右手画个普通DNN用于学习隐式的交叉特征,最终一起联合训练。xDeepFM这里包含三部分:普通的线性部分、CIN部分用于构造高阶交叉特征、普通的DNN部分用于学习隐式特征。
这里核心部分显然在于CIN结果,本篇博客会重点讲解这个部分。
三、xDeepFM中CIN网络结构
CIN全称Compressed Interaction Network,我们照着论文中给出的图逐一讲解,先上图:

3.1 图(a)
x 0 x^0 x0的维度为 m ∗ D m * D m∗D,m为特征个数,D为特征embedding向量维度。 x k x^k xk的维度为 H k ∗ D H_k*D Hk∗D, H k H_k Hk表示第 k k k层特征向量个数。它这里的做法是:用 x k x^k xk的第 i i i列向量即 x ∗ i k x^k_{*i} x∗ik与 x 0 x^0 x0的第 i i i列向量的转置即 ( x ∗ i 0 ) T (x^0_{*i})^T (x∗i0)T做外积,因此得到一个 H k ∗ m H_k*m Hk∗m大小的矩阵,因为总共有D个这些向量,所以最终结果也就是 Z k + 1 Z^{k+1} Zk+1为一个 H k ∗ m ∗ D H_k*m*D Hk∗m∗D的三维矩阵。
用个例子来说明上图,假设 x ∗ 1 k = [ a 1 , a 2 , a 3 ] x^k_{*1}=[a_1,a_2,a_3] x∗1k=[a1,a2,a3], x ∗ 1 0 = [ b 1 , b 2 , b 3 , b 4 ] x^0_{*1}=[b_1,b_2,b_3,b_4] x∗10=[b1,b2,b3,b4],则有:
x ∗ 1 k ⊗ ( x ∗ 1 0 ) T = [ a 1 a 2 a 3 ] ⊗ [ b 1 b 2 b 3 b 4 ] = [ a 1 b 1 a 1 b 2 a 1 b 3 a 1 b 4 a 2 b 1 a 2 b 2 a 2 b 3 a 2 b 4 a 3 b 1 a 3 b 2 a 3 b 3 a 3 b 4 ] \begin{aligned} x^k_{*1} \otimes (x^0_{*1})^T=\begin{bmatrix} a_1& a_2& a_3 \\ \end{bmatrix} \otimes \begin{bmatrix} b_1 \\ b_2 \\ b_3 \\ b_4 \end{bmatrix}=\begin{bmatrix} a_1b_1& a_1b_2& a_1b_3&a_1b_4 \\ a_2b_1& a_2b_2& a_2b_3&a_2b_4 \\ a_3b_1& a_3b_2& a_3b_3&a_3b_4 \\ \end{bmatrix} \end{aligned} x∗1k⊗(x∗10)T=[a1a2a3]⊗⎣⎢⎢⎡b1b2b3b4⎦⎥⎥⎤=⎣⎡a1b1a2b1a3b1a1b2a2b2a3b2a1b3a2b3a3b3a1b4a2b4a3b4⎦⎤
以此类推, x ∗ 2 k ⊗ x ∗ 2 0 x^k_{*2} \otimes x^0_{*2} x∗2k⊗x∗20, x ∗ 3 k ⊗ x ∗ 3 0 x^k_{*3} \otimes x^0_{*3} x∗3k⊗x∗30,…, x ∗ D k ⊗ x ∗ D 0 x^k_{*D} \otimes x^0_{*D} x∗Dk⊗x∗D0均会得到一个 H k ∗ m H_k*m Hk∗m的矩阵,合在一起变为一个 H k ∗ m ∗ D H_k*m*D Hk∗m∗D的三维矩阵,也就是上图中的 Z k + 1 Z^{k+1} Zk+1。
3.2 图(b)
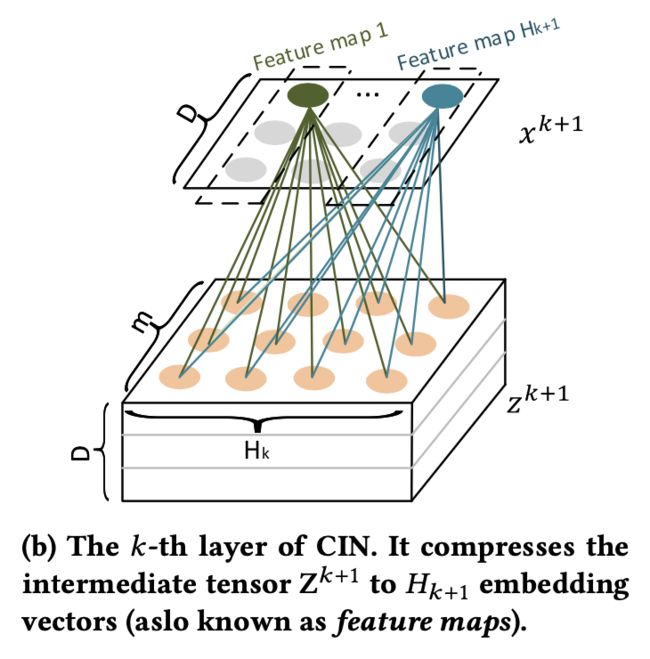
经过图(a)中的外积操作,我们得到一个 H k ∗ m ∗ D H_k*m*D Hk∗m∗D的三维矩阵 Z k + 1 Z^{k+1} Zk+1,图(b)要做的事情就是把一个 H k ∗ m ∗ D H_k*m*D Hk∗m∗D的矩阵压缩成一个 H k ∗ D H_k*D Hk∗D的矩阵,这也是CIN中C的来源,Compressed。
说到矩阵维度的压缩,自然就想到了CNN中的卷积操作,论文也借鉴了卷积的操作思想,我们来看看是怎么操作的:它这里使用了 H k + 1 H_{k+1} Hk+1个大小为 H k ∗ m H_k*m Hk∗m的向量(矩阵)对 Z k + 1 Z^{k+1} Zk+1做了一波点乘内积,此时得到是 H k + 1 H_{k+1} Hk+1个向量的第一个元素,因为 Z k + 1 Z^{k+1} Zk+1的channel为D,因此最终得到的 x k + 1 x^{k+1} xk+1为 H k + 1 H_{k+1} Hk+1个D维向量,因此 x k + 1 x^{k+1} xk+1的维度为 H k ∗ D H_k*D Hk∗D。这里需要理解的是 H k ∗ m H_k*m Hk∗m向量(filter)对 Z k + 1 Z^{k+1} Zk+1做点乘内积,得到的是一个值,即向量的某个元素。在原论文里对应 H k H_k Hk个 W k , h W^{k,h} Wk,h。
3.3 图(c)

图(c)这里把整个CIN部分做了个概览,原论文中把这个步骤往RNN的思想上靠了一波。 x k x^k xk的产生由它的上一层 x k − 1 x^{k-1} xk−1和初始的 x 0 x^0 x0共同决定,论文中给出了一个形式化的公式:
X h , ∗ k = ∑ i = 1 H k − 1 ∑ j = 1 m W i j k , h ( X i , ∗ k − 1 ∘ X j , ∗ 0 ) X_{h,*}^k=\sum_{i=1}^{H_{k-1}}\sum_{j=1}^{m}W_{ij}^{k,h}(X_{i,*}^{k-1} \circ X_{j,*}^0) Xh,∗k=i=1∑Hk−1j=1∑mWijk,h(Xi,∗k−1∘Xj,∗0)
拿 x 2 x^2 x2为例来看下全过程, x 0 x^0 x0与 x 1 x^1 x1先经过图(a)中的外积操作得到一个 H 1 ∗ m ∗ D H_1*m*D H1∗m∗D的矩阵 Z 2 Z^{2} Z2,然后 Z 2 Z^{2} Z2经过图(b)中的压缩(卷积)操作,得到维度为 H 2 ∗ D H_2*D H2∗D的矩阵 x 2 x^2 x2,该矩阵包含 H 2 H_2 H2个D维的向量。然后对这 H 2 H_2 H2个D维向量分别做sum pooling操作,如图(c)所示,因此, x 1 x_1 x1最终产生一个 H 1 ∗ 1 H_1*1 H1∗1维向量, x 2 x_2 x2产生一个 H 2 ∗ 1 H_2*1 H2∗1维向量,…, x k x_k xk产生一个 H k ∗ 1 H_k*1 Hk∗1维向量,最后合并成一个维度为 ∑ i = 1 k H i \sum_{i=1}^kH_i ∑i=1kHi维度的向量,与DNN向量再做联合训练。论文中形式化的定义为,假设 X k X^k Xk经过sum pooling后得到的向量为 p k p^k pk,则 p k = [ p 1 k , p 2 k , . . . , p H k k ] p^k=[p_1^k,p_2^k,...,p_{H_k}^k] pk=[p1k,p2k,...,pHkk],则整个CIN最终产生的向量为 p + = [ p 1 , p 2 , . . . . , p K ] p^+=[p^1,p^2,....,p^K] p+=[p1,p2,....,pK], p + p^+ p+的维度为 ∑ i = 1 K H i \sum_{i=1}^KH_i ∑i=1KHi。
3.4 代码实现
paddle官方给出的cin部分的实现代码为(我增加了tensor的维度注释,方便大家理解):
def forward(self, feat_embeddings):
# [shape=[5, 39, 9]]
Xs = [feat_embeddings]
last_s = self.num_field
# layer_sizes_cin=[128, 32]
# cnn_layers= [Conv2D(1521, 128, kernel_size=[1, 1], data_format=NCHW),
# Conv2D(4992, 32, kernel_size=[1, 1], data_format=NCHW)]
for s, _conv in zip(self.layer_sizes_cin, self.cnn_layers):
# 做外积,对应图(a)
# Tensor(shape=[5, 9, 39, 1])
X_0 = paddle.reshape(
# shape=[5,9,39]
x=paddle.transpose(Xs[0], [0, 2, 1]),
shape=[-1, self.sparse_feature_dim, self.num_field,
1]) # None, embedding_size, num_field, 1
# shape=[5, 9, 1, 39]
X_k = paddle.reshape(
x=paddle.transpose(Xs[-1], [0, 2, 1]),
shape=[-1, self.sparse_feature_dim, 1,
last_s]) # None, embedding_size, 1, last_s
# shape=[5, 9, 39, 39]
Z_k_1 = paddle.matmul(
x=X_0, y=X_k) # None, embedding_size, num_field, last_s
# 卷积操作,对应图(b)
# compresses Z^(k+1) to X^(k+1)
# shape=[5, 9, 1521]
Z_k_1 = paddle.reshape(
x=Z_k_1,
shape=[-1, self.sparse_feature_dim, last_s * self.num_field
]) # None, embedding_size, last_s*num_field
# shape=[5, 1521, 9]
Z_k_1 = paddle.transpose(
Z_k_1, [0, 2, 1]) # None, s*num_field, embedding_size
# shape=[5, 1521, 1, 9]
Z_k_1 = paddle.reshape(
x=Z_k_1,
shape=[
-1, last_s * self.num_field, 1, self.sparse_feature_dim
]
) # None, last_s*num_field, 1, embedding_size (None, channal_in, h, w)
# shape=[5, 128, 1, 9]
X_k_1 = _conv(Z_k_1)
# shape=[5, 128, 9]
X_k_1 = paddle.reshape(
x=X_k_1,
shape=[-1, s,
self.sparse_feature_dim]) # None, s, embedding_size
#X_k_1 = m(X_k_1)
Xs.append(X_k_1)
last_s = s
# 池化,图(c)
# sum pooling
# Xs-->Tensor(shape=[5, 39, 9]), Tensor(shape=[5, 128, 9]), Tensor(shape=[5, 32, 9]]
# shape=[5, 160, 9]
y_cin = paddle.concat(
x=Xs[1:], axis=1) # None, (num_field++), embedding_size
# shape=[5, 160]
y_cin = paddle.sum(x=y_cin, axis=-1) # None, (num_field++)i
tmp_sum = sum(self.layer_sizes_cin)
# shape=[5, 1]
y_cin = self.cin_linear(y_cin)
# shape=[5, 1]
return y_cin
四、联合训练目标函数
xDeepFM整体包含三部分:线性部分、CIN部分、DNN部分。论文给出了联合训练的交叉熵损失函数:
L = − 1 N ∑ i = 1 N y i l o g y i ^ + ( 1 − y i ) l o g ( 1 − y i ^ ) L=-\frac{1}{N}\sum_{i=1}^Ny_ilog\hat{y_i} + (1-y_i)log(1-\hat{y_i}) L=−N1i=1∑Nyilogyi^+(1−yi)log(1−yi^)
其中,预测输出 y i ^ = σ ( W l i n e a r T a + W d n n T x d n n k + W c i n T p + + b ) \hat{y_i}=\sigma(W^T_{linear}a + W^T_{dnn}x^k_{dnn} + W^T_{cin}p^+ +b) yi^=σ(WlinearTa+WdnnTxdnnk+WcinTp++b),即把三部分想加然后做sigmoid。
五、总结
个人认为xDeepFM参数量较大,计算复杂度应该相对较高,在真实的场景下性能可能会成为一个问题。至于效果,在不同的数据集下与其他模型可能会呈现出不同的结果,例如DCN V2论文里给出的实验结果,xDeepFM在AUC指标上在一些数据集上效果还不如DCN。有兴趣的可以直接去看DCN V2这篇论文的实验比较部分,DCN V2论文地址:DCN V2。
参考文献
- Lian J, Zhou X, Zhang F, et al. xdeepfm: Combining explicit and implicit feature interactions for recommender systems[C]//Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining. 2018: 1754-1763.
- Wang R, Shivanna R, Cheng D, et al. DCN V2: Improved deep & cross network and practical lessons for web-scale learning to rank systems[C]//Proceedings of the Web Conference 2021. 2021: 1785-1797.
