三.过/欠拟合，梯度爆炸/消失

1.1过拟合和欠拟合

接下来，我们将探究模型训练中经常出现的两类典型问题：

一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）；
另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。
在实践中，我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题，在这里我们重点讨论两个因素：模型复杂度和训练数据集大小。

1.2模型复杂度

为了解释模型复杂度，我们以多项式函数拟合为例。给定一个由标量数据特征和对应的标量标签组成的训练数据集，多项式函数拟合的目标是找一个阶多项式函数

来近似。在上式中，是模型的权重参数，是偏差参数。与线性回归相同，多项式函数拟合也使用平方损失函数。特别地，一阶多项式函数拟合又叫线性函数拟合。

给定训练数据集，模型复杂度和误差之间的关系：

image

1.3训练数据集大小

影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，例如层数较多的深度学习模型。

1.4权重衰减

方法

权重衰减等价于范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。

L2 范数正则化（regularization）

范数正则化在模型原损失函数基础上添加范数惩罚项，从而得到训练所需要最小化的函数。范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以线性回归中的线性回归损失函数为例

其中是权重参数，是偏差参数，样本的输入为，标签为，样本数为。将权重参数用向量表示，带有范数惩罚项的新损失函数为

其中超参数。当权重参数均为0时，惩罚项最小。当较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当设为0时，惩罚项完全不起作用。上式中范数平方展开后得到。
有了范数惩罚项后，在小批量随机梯度下降中，我们将线性回归一节中权重和的迭代方式更改为

$\begin{aligned} w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\ w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right). \end{aligned}$

可见，范数正则化令权重和先自乘小于1的数，再减去不含惩罚项的梯度。因此，范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。

1.5丢弃法

多层感知机中神经网络图描述了一个单隐藏层的多层感知机。其中输入个数为4，隐藏单元个数为5，且隐藏单元（）的计算表达式为

这里是激活函数，是输入，隐藏单元的权重参数为，偏差参数为。当对该隐藏层使用丢弃法时，该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为，那么有的概率会被清零，有的概率会除以做拉伸。丢弃概率是丢弃法的超参数。具体来说，设随机变量为0和1的概率分别为和。使用丢弃法时我们计算新的隐藏单元

由于，因此

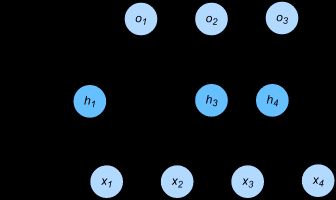
即丢弃法不改变其输入的期望值。让我们对之前多层感知机的神经网络中的隐藏层使用丢弃法，一种可能的结果如图所示，其中和被清零。这时输出值的计算不再依赖和，在反向传播时，与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的，即都有可能被清零，输出层的计算无法过度依赖中的任一个，从而在训练模型时起到正则化的作用，并可以用来应对过拟合。在测试模型时，我们为了拿到更加确定性的结果，一般不使用丢弃法

image

2.梯度消失和梯度爆炸

深度模型有关数值稳定性的典型问题是消失（vanishing）和爆炸（explosion）。

当神经网络的层数较多时，模型的数值稳定性容易变差。

假设一个层数为的多层感知机的第层的权重参数为，输出层的权重参数为。为了便于讨论，不考虑偏差参数，且设所有隐藏层的激活函数为恒等映射（identity mapping）。给定输入，多层感知机的第层的输出。此时，如果层数较大，的计算可能会出现衰减或爆炸。举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知机的第30层输出为输入分别与（消失）和（爆炸）的乘积。当层数较多时，梯度的计算也容易出现消失或爆炸。

2.1随机初始化模型参数

在神经网络中，通常需要随机初始化模型参数。下面我们来解释这样做的原因。

回顾多层感知机一节描述的多层感知机。为了方便解释，假设输出层只保留一个输出单元（删去和以及指向它们的箭头），且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有1个隐藏单元在发挥作用。因此，正如在前面的实验中所做的那样，我们通常将神经网络的模型参数，特别是权重参数，进行随机初始化。

Image Name

2.2PyTorch的默认随机初始化

随机初始化模型参数的方法有很多。在线性回归的简洁实现中，我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过，PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略（不同类型的layer具体采样的哪一种初始化方法的可参考源代码），因此一般不用我们考虑。

2.3Xavier随机初始化

还有一种比较常用的随机初始化方法叫作Xavier随机初始化。
假设某全连接层的输入个数为，输出个数为，Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布

它的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层输出个数影响。