【Matplotlib】条形图与直方图
文章目录
- 垂直条形图
-
- 代码
- 运行结果
- 代码分析
- 水平条形图
-
- 代码
- 运行结果
- 并列条形图
-
- 代码
- 运行结果
- 代码分析
- 条纹填充并列条形图
-
- 代码
- 运行结果
- 代码分析
- 叠加条形图
-
- 代码
- 运行结果
- 代码分析
- 直方图
-
- 绘制频率分布直方图
-
- 代码
- 运行结果
- 代码分析
- 利用hist()返回值美化直方图
-
- 代码
- 运行结果
- 代码分析
垂直条形图
代码
import numpy as np
import matplotlib.pyplot as plt
objects = ('Python', 'C++', 'Java', 'Perl', 'Scala', 'Lisp')
y_pos = np.arange(len(objects))
performance = [10, 8, 6, 4, 2, 1]
plt.bar(y_pos, performance, align='center', alpha=0.5)
plt.xticks(y_pos, objects)
plt.ylabel('用户量')
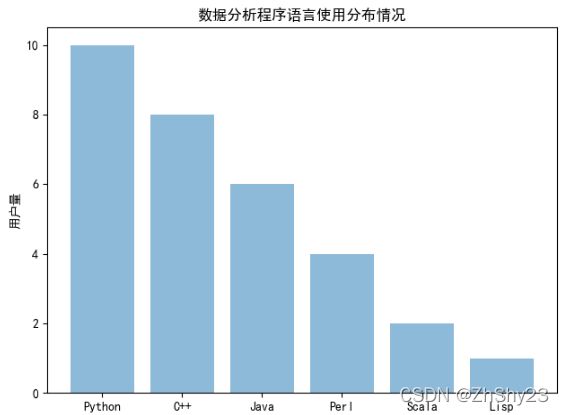
plt.title('数据分析程序语言使用分布情况')
plt.show()
运行结果
代码分析
plt.bar()函数参数:
- left:X轴的位置序列,一般采用arange()函数产生一个序列,见本例第05行代码。
- height:Y轴的数值序列,也就是条形图的高度,一般就是我们需要显示的数据。见本例第06行代码。本例中所表达的程序设计语言使用情况,仅仅是为了说明一个条形图如何绘制而杜撰的数字,不可较真。
- width:条形图的宽度,取值范围为0~1,默认为0.8(相对缩小)。
- bottom:条形图的起始位置,也是Y轴的起始坐标。默认值为None(即以X轴作为起点),如果为叠状条形图,该值通常为次一级条形图的高度。
- alpha:透明度,其取值范围为0~1。0为全透明,1为不透明。本例取值0.5,读者可根据情况自行调整。
- color或facecolor:条形图填充的颜色。取值可以为rbg#123465等,默认为b。这里的b表示blue(蓝色)。如果是黑色的话,简写为k。
- edgecolor:图形边缘的颜色。
- Linewidth、linewidths或lw:图形边缘线的宽度。
- tick_labe:设置每个刻度处的标签。在本例中,一方面可以在bar参数中设置tick_label=objects。另一方面,也可以单独设置,如本例第09行的plt.xticks(y_pos, objects)。二者功能相同。
- label:标签,当有多个条形图并列时,可以区分不同条形图代表的含义。
水平条形图
将上例第8行改成:
plt.barh(y_pos, performance, align='center', alpha=0.5)
代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
objects = ('Python', 'C++', 'Java', 'Perl', 'Scala', 'Lisp')
y_pos = np.arange(len(objects))
performance = [10, 8, 6, 4, 2, 1]
plt.barh(y_pos, performance, align='center', alpha=0.5, color='k', tick_label=objects)
plt.xlabel('用户量')
plt.title('数据分析程序语言使用分布情况')
plt.show()
运行结果
并列条形图
代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 绘图
n_group = 4
means_frank = (90, 55, 40, 65)
means_guido = (85, 62, 54, 20)
# 创建图像
fig, ax = plt.subplots()
# 定义条形图在横坐标上的分类位置
index = np.arange(n_group)
bar_width = 0.35
opacity = 0.8
rectsl = plt.bar(index,
means_frank,
bar_width,
alpha=opacity,
color='b',
label='张三')
rects2 = plt.bar(index + bar_width,
means_guido,
bar_width,
alpha=opacity,
color='g',
label='李四'
)
plt.xlabel('课程')
plt.ylabel('分数')
plt.title('分数对比图')
plt.xticks(index + bar_width, ('A', 'B', 'C', 'D'))
plt.legend()
plt.show()
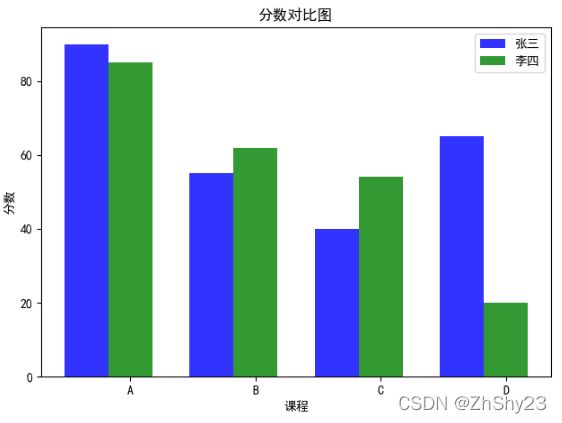
运行结果
代码分析
在本质上,垂直并列条形图就是在X轴上分别画两组并列的条形图,但二者在X轴的位置上有先后关系。举例来说,代码第20~25行画出了第一个条形图。请注意,实际上代码第20~25行是一行语句,不过是为了注释方便,将不同的参数放置于不同的行罢了。
代码第27~31行画出了第二个条形图。值得注意的是,在细节处理上,它的X轴坐标的向右偏移量正好等于第一个条形图的宽度,通过X轴上的偏移操作index+bar_width,第二个条形图能与第一个条形图在X轴上无缝“肩并肩”。
为了区分两组条形图,我们用label属性(见代码第25行和第31行)来区分不同图形的标签。
我们知道,即使不同的条形图使用了不同颜色加以区分,但有时效果也欠佳。这是因为,在彩色的电子显示设备中,这些多彩图形清晰可分,但当黑白打印时,颜色往往难以区分。
因此,在科技论文写作中,常常使用不同纹理而非不同颜色来区分不同的条形图。这时,就需要使用条形图的hatch(填充)参数了。下面,我们接着改写前面的范例,绘制带有纹理填充的条形图。
条纹填充并列条形图
代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 绘图
n_group = 4
means_frank = (90, 55, 40, 65)
means_guido = (85, 62, 54, 20)
# 创建图像
fig, ax = plt.subplots()
# 定义条形图在横坐标上的分类位置
index = np.arange(n_group)
bar_width = 0.35
opacity = 0.8
rectsl = plt.bar(index,
means_frank,
bar_width,
alpha=opacity,
color='w', edgecolor='k',
hatch='......',
label='张三')
rects2 = plt.bar(index + bar_width,
means_guido,
bar_width,
alpha=opacity,
color='w', edgecolor='k',
hatch='\\\\',
label='李四'
)
plt.xlabel('课程')
plt.ylabel('分数')
plt.title('分数对比图')
plt.xticks(index + bar_width, ('A', 'B', 'C', 'D'))
plt.legend()
plt.show()
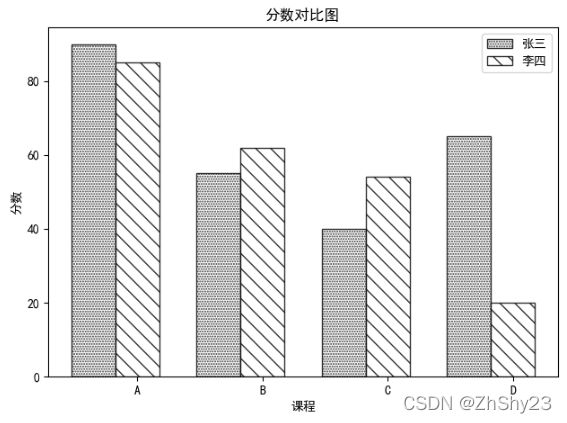
运行结果
代码分析
本例的绘图关键在于,首先要将图形的填充色设置为白色:color=“w”。同时把图形的边界颜色设置为黑色:edgecolor=“k”。最后我们再设置图形的纹理。
参数hatch可用来设置填充的纹理类型,其可取值为/、\、|、-、+、x、o、O、.、*。这些符号表示图形中填充的符号,大多都能“见号知意”。
这里有一个小技巧,即你使用的填充单一符号越多,图形中对应的纹理就越密集,例如,通过第24行的hatch=’…‘绘制的图形就比通过hatch=’…‘绘制的图形纹理更密集,这个填充符号表示图形里面填充的都是点(.)。同理,第32行的hatch=’\\’,就比hatch=’\‘纹理密集,这里表示填充的是反斜线。
最后需要说明的是,注意转义字符的干扰。如果我们在第32行的字符串前添加一个字符r,即变为hatch=r’\\’,则图8-20中条形图的斜线纹理要密集得多.
叠加条形图
代码
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
# 绘图
n_group = 4
means_frank = (90, 55, 40, 65)
means_guido = (85, 62, 54, 20)
# 创建图像
fig, ax = plt.subplots()
# 定义条形图在横坐标上的分类位置
index = np.arange(n_group)
bar_width = 0.35
opacity = 0.8
rectsl = plt.bar(index,
means_frank,
bar_width,
alpha=opacity,
color='w', edgecolor='k',
hatch='......',
label='张三')
rects2 = plt.bar(index,
means_guido,
bar_width,
bottom=means_frank, ###############
alpha=opacity,
color='w', edgecolor='k',
hatch='\\\\',
label='李四'
)
plt.xlabel('课程')
plt.ylabel('分数')
plt.title('分数对比图')
plt.xticks(index + bar_width, ('A', 'B', 'C', 'D'))
plt.legend()
plt.show()
运行结果
代码分析
在本例中,成功绘图的关键有两点:首先,第一个条形图和第二个条形图的X轴坐标是一样的;其次,第二个条形图的Y轴坐标是站在第一个肩膀上的,第二个条形图是以第一个为底(bottom)的。于是,顺理成章地,如果我们还有第三个条形图需要叠加的话,它的起点是第二个条形图的顶点,以此类推。
直方图
前面我们讨论了条形图的绘制。如前所述,条形图一般用来描述顺序数据,其中的各个长条形之间留有空隙,以区分不同的类别,不同的类别之间没有必然的先后关系,调整彼此的顺序,并不会影响数据的可视化表达。
对比而言,直方图(Histogram)则像一种统计报告图。在外观上,它也由一个个的长条形构成,但直方图在宽度(即X轴)方向将样本的取值范围从小到大划分为若干个间隔(bin),这个间隔越大,表明涵盖的属性值跨度就越大(换句话说,间隔并不必须是等分的)。在高度(即Y轴)方向,直方图可表示特定间隔区间样本出现的次数(即频数),长条形越高,表明此间隔内的样本越多。换句话说,直方图的宽度和高度均有意义,特别是在宽度方向,“尊卑有序”,不可随意调整顺序。
为了构建直方图,第一步是将样本在某个特定属性的取值范围内进行分段,形成一系列间隔,然后计算每个间隔中有多少个样本。下面我们用范例来说明如何绘制频率分布直方图。
绘制频率分布直方图
代码
import numpy as np
import matplotlib.pyplot as plt
mu = 100
sigma = 15
x = mu + sigma * np.random.randn(200)
num_bins = 25
plt.figure(figsize=(9, 6), dpi=100)
n, bins, patches = plt.hist(x, num_bins,
color="w", edgecolor="k",
hatch=r'ooo',
density=1,
label='频率')
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu)) ** 2))
plt.plot(bins, y, '--', label='概率密度函数')
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.xlabel('聪明度')
plt.ylabel('概率密度')
plt.title('IQ直方图:$\mu = 100$, $\sigma = 15$')
plt.legend()
plt.show()
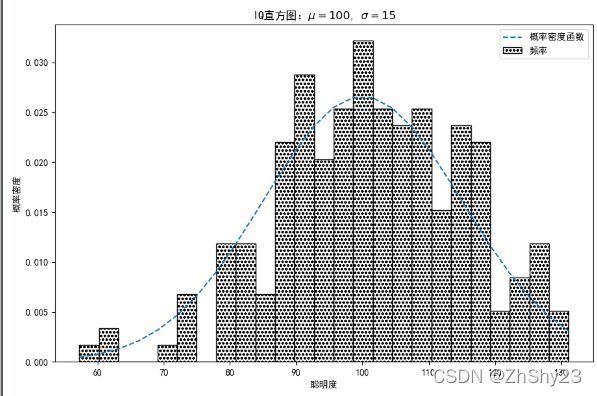
运行结果
代码分析
代码第06行使用np.random.randn()函数随机生成期望为100,标准差为15的200个数据,num_bins表示划分的组数。本例中的核心函数是hist(),其原型如下所示。
hist(
x, bins=None, range=None, density=None, weights=None,
cumulative=False, bottom=None, histtype='bar', align='mid',
orientation='vertical', rwidth=None, log=False, color=None,
label=None, stacked=False, normed=None, *, data=None,
**kwargs):
参数:
- x:指定要在X轴上绘制直方图所需的数据;在形式上,它可以是一个数组,也可以是数组序列。如果是数组序列,数组的长度不需要相同。
- bins:指定直方图条形的个数。如果此处的值为整数,就会产生bins+1个分割边界,此时该方法就等价于numpy.histogram,默认值为10,即将属性值10等分。如果该值是一个序列,则可构建一个非分等的间隔序列,如取值为[1, 3, 4,6],表示第一个间隔区间是[1,3),请注意此时区间范围为左闭右开,即第一个分割区间不包括上界3。类似地,第二个间隔区间是[3,4)。但是最后一个间隔由于没有下一个间隔来“接盘”,所以是完全的闭区间,即[4,6]。
- range:设置直方图数据的显示上、下界,边界之外的数据将被舍弃。默认为None,即不设置边界,包含所有数据。
- density:可选项,是一个布尔值,用于设置是否进行归一化处理。如果为True,返回元组的第一个元素并将把计数标准化为一个概率密度,也就是说,直方图下的面积(或积分)总和为1。
- weights:为每一个数据点设置权重。
- cumulative:表明是否需要计算累计频数或频率。
- bottom:为直方图的每个条形添加基准线,默认为0。
- histtype:指明直方图的类型,可选bar、barstacked、step、stepfilled中的一种,默认为bar,即条形图。
- align:设置条形边界的对齐方式,默认为mid,除此之外还有left和right。
- normed:表明是否将得到的直方图向量归一化,布尔类型,默认为False。
- orientation:指明直方图中条形的呈现方向,要么水平,要么垂直。因此可选值为horizontal、vertical,默认值为垂直方向(horizontal)。
- rwidth:设置直方图各条形宽度的百分比,默认是0。
- log:指明是否需要对绘图数据进行对数(log)变换。
- color:设置直方图的填充色。
- label:设置直方图的标签,可展示图例。
- stacked:指明当有多个数据时,是否需要将直方图呈堆叠摆放,默认设置是水平摆放。
- normed:指明是否将直方图的频数转换成频率(已弃用,被density替代)。下面我们再来看一下hist()函数的返回值,分别如下。
- n:直方图每个间隔内的样本数量,数据形式为数组或数组列表。
- bins:返回直方图中各个条形(分组)的区间范围,数据形式为数组。
- patches:返回直方图中各个间隔的相关信息(如颜色、透明度、高度、角度等),数据形式为列表或列表的列表(即嵌套列表,相当于多维数组)。
利用hist()返回值美化直方图
代码
import matplotlib.pyplot as plt
import numpy as np
x = np.random.normal(0, 1, 5000) # 生成正态分布的5000个随机样本
plt.figure(figsize=(14, 7)) # 设置图片大小 14*7inch
plt.style.use('seaborn-whitegrid') # 设置绘图风格
n, bins, patches = plt.hist(x, bins=90, facecolor='#2ab0ff',
edgecolor='#169acf', linewidth=0.5)
n = n.astype('int') # 返回值n必须是整型
# 设置显示中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 显示负号
# 为每个条形设置颜色
for i in range(len(patches)):
patches[i].set_facecolor(plt.cm.viridis(n[i] / max(n)))
# 对某个特定条形做特别说明
patches[49].set_fc('red') # 设置颜色
patches[49].set_alpha(1) # 设置透明度:不透明
# 添加注释
plt.annotate('这是一个重要条形!', xy=(0.6, 155), xytext=(1.5, 130), fontsize=15,arrowprops={'width': 0.4, 'headwidth': 5, 'color': '#333333'})
# 设置x轴和y轴的标题、字体
plt.title('正态分布', fontsize=12)
plt.xlabel('不同的间隔(bins)', fontsize=10)
plt.ylabel('频度大小', fontsize=10)
plt.show()
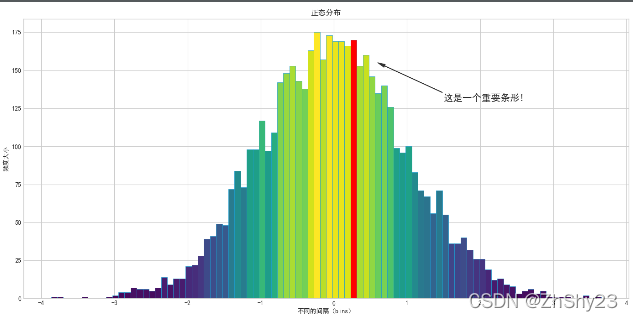
运行结果
代码分析
在本例中,我们利用NumPy生成了5000个服从正态分布的随机样本点(第03行),然后通过直方图来可视化它们的分布。第06行除了绘制普通的直方图,更重要的是返回了是三个参数。
本例中的关键之处在于,不同的patch参数代表不同间隔(bin)的构造信息,第13~14行为每个patch设置了不同的前置色。第16~17行为特定的patch设置了填充色和透明度。
第19行是一个绘图小技巧,即利用annotate()方法在图形上给数据添加文本注解,以方便我们在合适的位置添加描述信息。