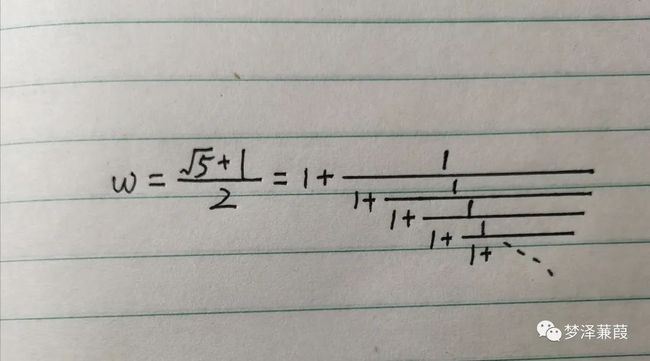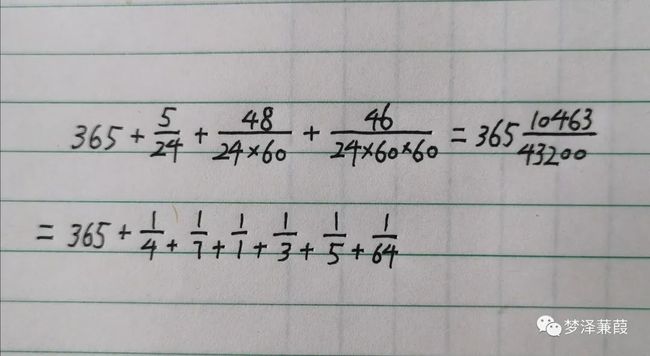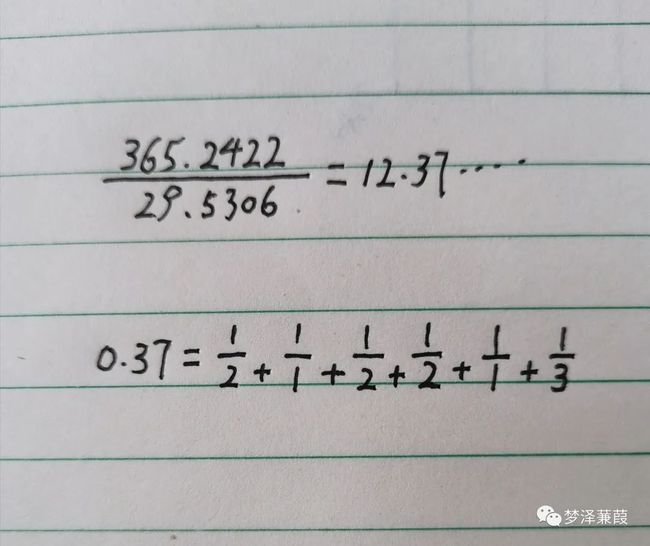连分数是一个有趣的数论问题,不仅在纯数学领域有很多值得探讨的东西,还有着广泛的应用。在此,对连分数的几何意义进行一些讨论,不仅比抽象的算术方法更直观、简明,还能引发一些有趣的思考。
连分数的几何表示,只需举一个无理数 ω=(√5+1)/2的例子说明。下图是ω=(√5+1)/2的连分数展开式:
如果我们在第零、一、二、三、四、五……个偏分母之后停止展开,就会得到一系列有理分数1、2、3/2、5/3、8/5、13/8……这些有理分数称作收敛子,最一般的表示记作pn/qn。
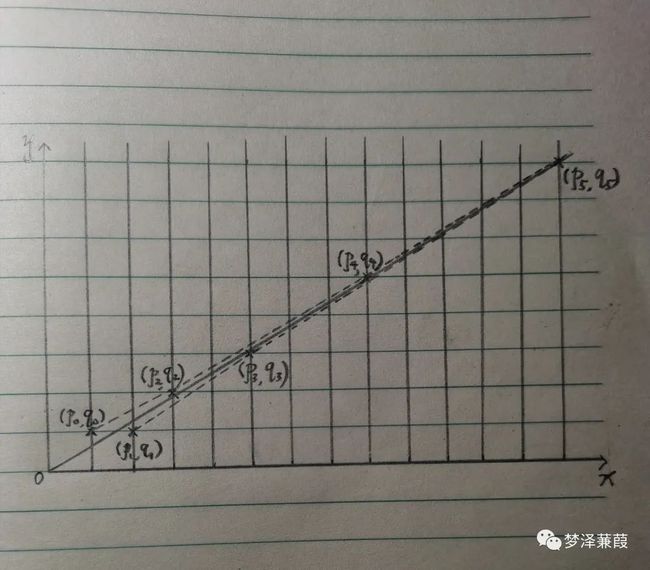
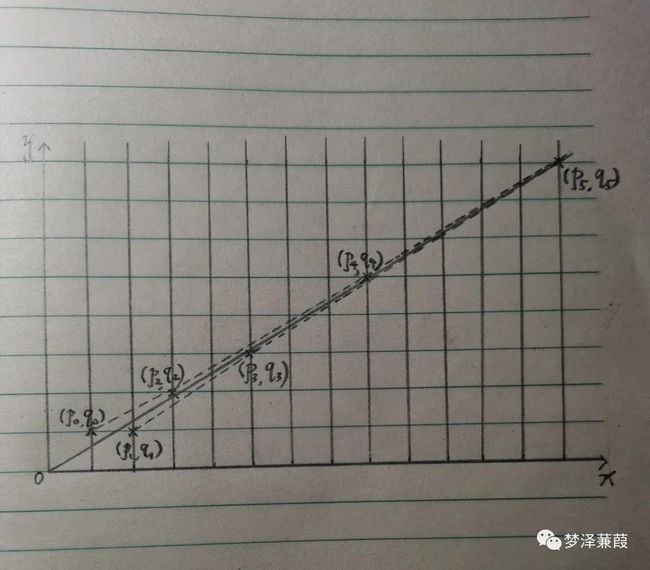
为了用几何图形把连分数展开表示出来,我们不妨在xy平面第一象限内画出“网格”,“网格”的那些交点就是一切有整坐标的点。同时,把收敛子pn/qn换一种表示方法,分子作为横坐标,分母作为纵坐标,即(pn,qn),这样,任意有理数都和网格的交点一一对应。很容易把以上收敛子在“网格”上标出,如下图所示:
然后,我们把ω=(√5+1)/2表示为一条无理射线ω=x/y,所谓无理射线,除了原点o之外,射线上没有一个横纵坐标同为整数的整点。从图中可以看到,(p0,q0)、(p2,q2)、(p4、q4)…从射线左侧越来越趋近于射线ω=x/y;(p1,q1)、(p3,q3)、(p5、q5)…从右侧趋近ω=x/y。这就是几何化的连分数定义,十分简明直观,其中也有许多值得讨论的东西:
首先,我们在图中画出的是无理射线,所以收敛子不可能落在该射线上,趋近过程会左右交替无限进行下去。反之,如果画出的是有理射线,当一个收敛子落在射线上时,这个过程也就在有限步之后终止,对应的算术过程就是反复相除得到的余数为零。关于分别趋近有理数和无理数,可以举两个经典的例子:
一个是关于历法。众所周知,平日里用的阳历每隔四年一个闰年,即增加一天,一个回归年是365天5小时48分46秒,对其进行连分数展开如下:
进行连分数运算后,可知分数部分的收敛子分别是1/4、7/29、8/33、31/128、163/673、10463/43200。这说明每4年加1天是最方便的逼近,而每29年加7天则更精密些,每33年加8天精密程度更高……依次进行,可以不断把历法制定得更精确。例如,每33年加8天,每99年就是加24天,所以虽然每四年一闰,到了第一百年却要少闰一天。
我国传统的历法所谓“阴历”、“农历”,其实是以回归年范导月相周期的阴阳混合历。为了解决前者非后者整数倍的问题,先民们想出了巧妙的“置闰”。月亮绕地球一周的时间是29.5306天,用连分数展开闰月的问题一目了然:
如图,计算可得收敛子依次为1/2、1/3、3/8、7/19、10/27。由于是左右交替逼近,也就是说,设置闰月,两年一闰太多,三年一闰太少,八年三闰太多,十九年七闰太少……。
对于图中无理射线的情况,最有名的例子当属圆周率的连分数展开:
收敛子22/7、355/113分别就是祖冲之用来近似表达圆周率的约率和密率。
除前述例子之外,涉及几个不同的周期相遇或者说重迭的问题,比如天体的相冲、合璧、联珠,各种波动的叠加甚至齿轮的嵌合等等,连分数都可能作为一个有用的工具。从这些例子中,我们可以抽象出一个称为丢番图逼近的逼近论问题,表述如下:
给定一正实数r,再给定一个自然数N,求一个分母不大于N的有理数p/q,使r-p/q的绝对值最小。
需要特别指出的是,每个收敛子都比任何一个分母不比它大的有理数更接近实数r,这是连分数有重大应用价值的前提。用代数或者算术的方法详细探讨丢番图逼近,过程十分繁琐且不易理解,有兴趣的话可以参考相关的数论教科书。反之,如果用刚才讨论过的几何表示,则十分直观易懂。
如图,我们可以假想在所有整点上都钉上钉子,用两根细线从射线ω=x/y出发分别向左和向右拉紧,则形成一系列围绕左右两个整点集的凸多边形的顶点。在拉紧的过程中,细线最先碰到的钉子就是对无理数ω的最近似的逼近,依次变得粗疏。而且容易直观到,对于凸多边形的这些顶点,纵坐标(即分母)相同或者更小的所有钉子,都不可能比顶点更接近射线ω=x/y。
我们可以从更高的数学观点来看待丢番图逼近的问题。该逼近论的深刻之处在于指出,任何一个实数(当然包括无理数)可以表为一个有理数序列的极限,换个角度讲,有理数域对于极限运算不是自封的。从数域扩张的角度看,这也给了我们把有理数域扩张到实数域的理由。而以实数为元素的序列就不可能通过取极限而得出实数以外的新数来,也就是说一旦扩张到实数域,对极限运算就是自封的了。数的连续统是极限概念的基础,也相互成就,从17世纪以来就成了解析几何和分析学的基础,不过当时并不是在经过严格的审查和分析之后才被接受的。
在连分数几何表示的图中,一直没有被我们注意到的是,射线ω=x/y上除了o之外没有一个整点,这其实足以让人惊讶。我们知道,把无理数定义为有理数的一个分割的所谓戴德金分割,是数学史上具有里程碑意义的一个经典定义。在这个几何表示中,射线ω=x/y就是整点即有理数对场上的一个分割,左右两侧的点集向着该分割收敛。一维的戴德金分割十分抽象,一旦扩展到如此的二维情形,就豁然开朗很多,甚至可以直观到其中的过程。这和许多模糊而模棱两可的数学问题——例如,泰勒展开中,为何在函数完全解析的地方幂级数却突然不再收敛——一旦拓展到复平面就豁然开朗异曲同工。
最后需要指出,数论大家高斯和狄利克莱都是通过几何图形研究数论的高手,可后来越来越依靠抽象的算术方法。很多问题如果从数学史的自然发展顺序来理解,不仅顺理成章、水到渠成,而且还更容易挖掘出背后的数学甚至哲学思想,纵横发散,融会贯通,连分数就是一个经典的例子。