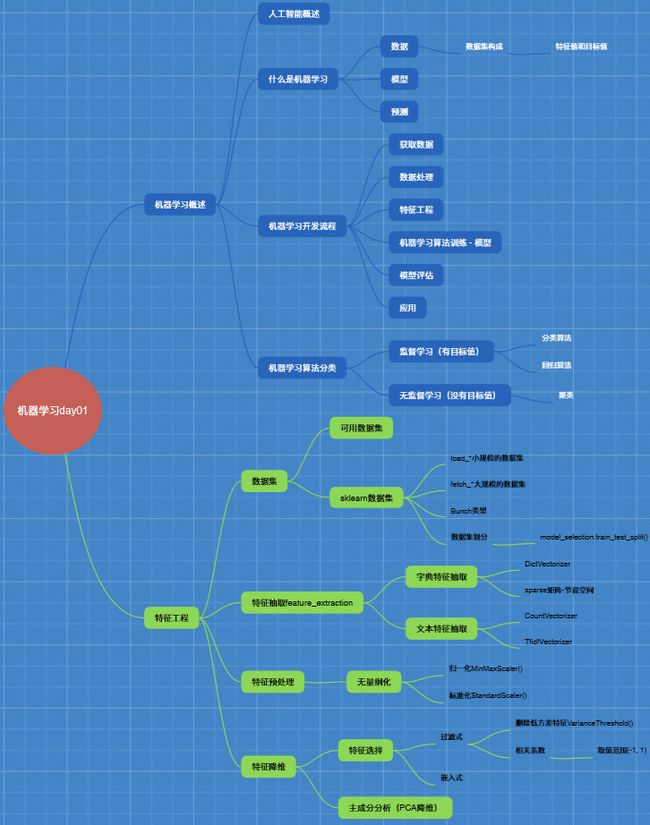
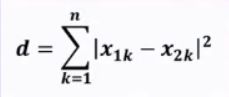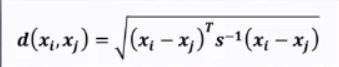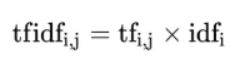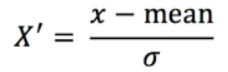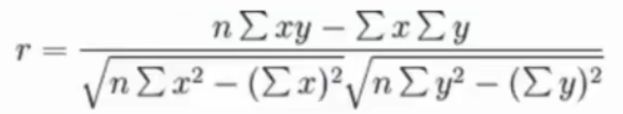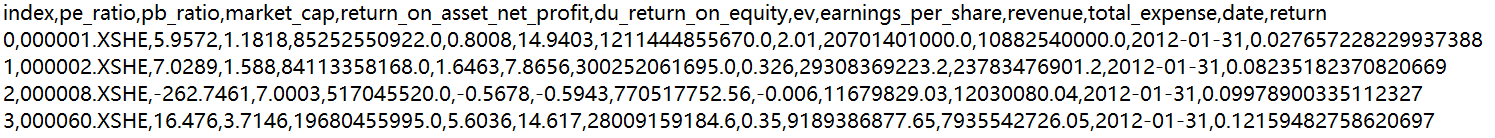机器学习入门

人工智能小案例：

请使用科学上网工具打开链接

案例一：https://quickdraw.withgoogle.com/

案例二：https://pjreddie.com/darknet/yolo/

案例三：https://deepdreamgenerator.com/

人工智能的发展历程：

图灵测试：

测试者与被测试者（一个人和一台机器）隔开的情况下，通过一些装置（如键盘）向被测试者随意提问。多次测试（一般为5min之内），如果有超过30%的测试者不能确定被测试者是人还是机器 ，那么这台机器就通过了测试，并被认为具有人类智能。

达特茅斯会议 ——人工智能的起点

时间：1956年8月，地点：美国汉诺斯小镇

参与人物：约翰·麦卡锡 马文·闵斯基（人工智能与认知学专家） 克劳德·香农（信息论的创始人） 艾伦·纽厄尔（计算机科学家） 赫伯特·西蒙（诺贝尔经济学奖得主）

众科学家聚在一起，讨论着一个完全不食人间烟火的主题。人工智能这个名字就是在这个时间产生的。因此，1956年也就称为人工智能元年。

第一个黄金时期（1956-20世纪70年代）

美国国防部赞助MIT222万美金，之后每年300万美金；

1963年斯坦福第一个AI实验室成立

第二个黄金时期（1956-20世纪70年代）

日本的第五代计算机项目拨款8.5亿美金；

1986，误差反向传播（BP）算法诞生

第一个低谷时期（20世纪70年代至80年代初）

James Lighthill：《Artificial Intelligence：A general survey》

专家系统：“知识期”

第二个低谷期（20世纪80年代至90年代初）

IBM与Apple普通台式机性能超过“智能计算机”

1991，日本的第五代计算机宣告失效

真正发展起来：

1980年代是正式成形期，1990-2010是蓬勃发展期，2012年之后是深度学习期。

人工智能的主要分支：

计算机视觉

语音识别：面临的难题—“鸡尾酒会效应”

百度语音识别：距离小于1m，中文字准率是97%

支持耳语、长语音、中英文混合及方言

文本挖掘/分类：

任务：句法分析、情绪分析、垃圾信息检测

比如，分析用户对外卖订单的评价，

机器翻译：

以前的翻译很垃圾，2014年开发的神经机器翻译（NMT）才让机器翻译很不错

机器人：工业机器人（机械臂）、家庭机器人（聊天、讲故事、打扫卫生、机器人女友）

2.机器学习算法分类

监督学习（Supervised Learning）：从给定的训练数据集中学习出一个函数，当新的数据到来时，根据这个函数预测结果。训练集通常由人工标注。

——————————————————————————————————————————
问题1：

特征值：猫/狗的图片 目标值：猫/狗 类别（离散型数据）

—>分类问题

问题2：

特征值：房屋的各个属性信息（朝向、面积、楼层）… 目标值：房屋价格（连续性数据）

—>回归问题

——————————————————————————————————————————

无监督学习（Unsupervised Learning）：与监督学习相比，训练集是无人为标注的结果。

——————————————————————————————————————————

问题3：

特征值：人物的各个属性信息 目标值：无

——————————————————————————————————————————

总结：

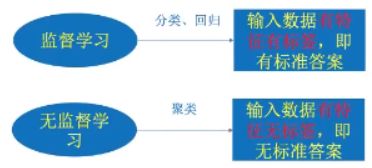
监督学习

定义：输入数据是有特征值和目标值所组成，函数的输出可以是一个连续的值（称为回归），或是输出有限个函数值（称作分类）。

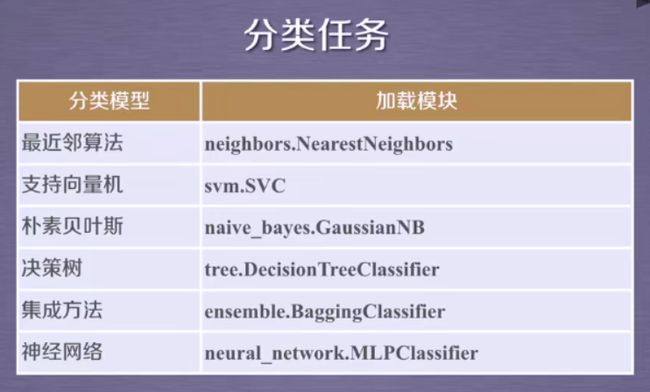
分类问题算法：k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归

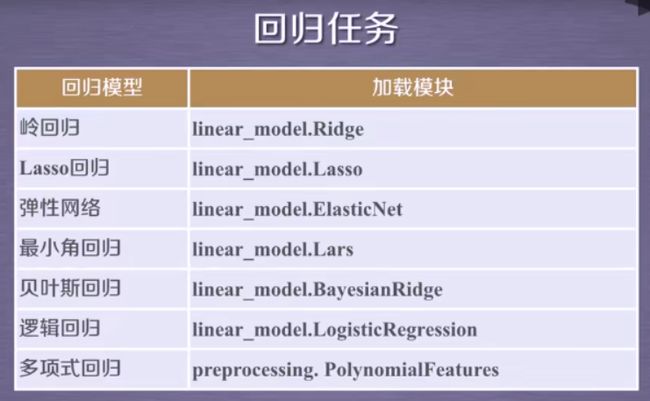
回归问题算法：线性回归、岭回归

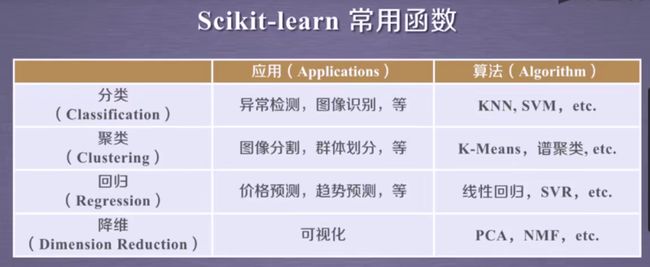
聚类问题算法：

降维问题算法：

无监督学习

定义：利用无标签的数据学习数据的分布或数据与数据之间的关系被称为无监督学习，即输入数据是由输入特征值所组成。

算法：聚类k-means

有监督学习和无监督学习的最大区别在于数据是否有标签。

无监督学习最常应用的场景是聚类（clustering）和降维（Dimension Reduction）

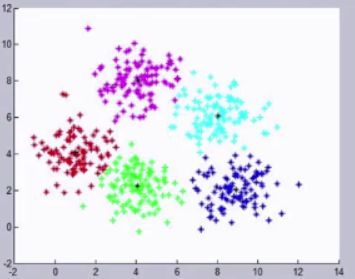
聚类：就是根据“数据的相似性”将数据分为多类的过程。评估两个不同样本之间的“相似性”，通常使用的方法就是计算两个样本之间的“距离”。使用不同的方法计算样本间的距离会关系到聚类结果的好坏。

常用的距离计算方法：

~欧氏距离：欧氏距离是最常用的一种距离度量方法，源于欧氏空间中两点的距离。

欧氏距离的计算公式：

~曼哈顿距离：曼哈顿距离也称为“城市街区距离”，类似于在城市之中驾车行驶，从一个十字路口到另外一个十字路口的距离。

曼哈顿距离的计算公式：

~马氏距离：马氏距离表示数据的协方差距离，是一种尺度无关的度量方式。也就是说马氏距离会先将样本点的各个属性标准化，再计算样本间的距离。

马氏距离的计算公式：

s为协方差矩阵

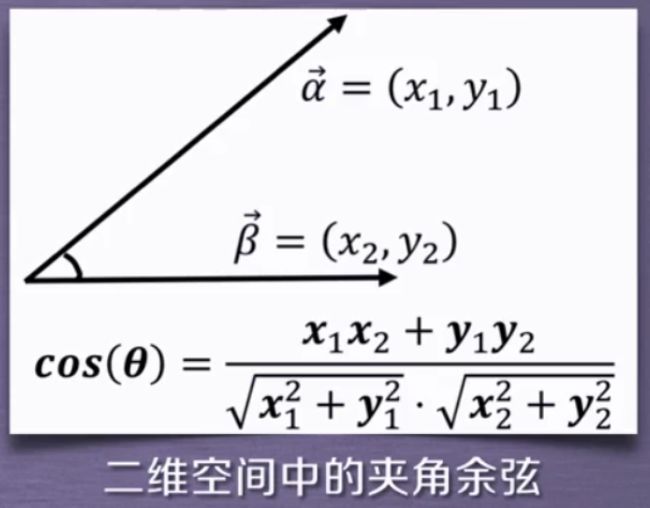
~夹角余弦：余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1，说明两个向量夹角越接近0度，表明两个向量越相似。

夹角余弦的计算公式：

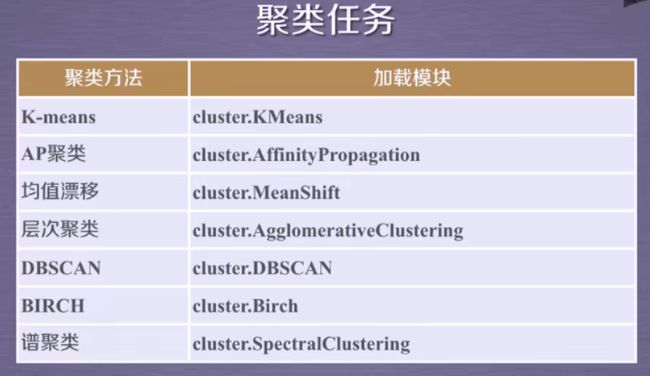
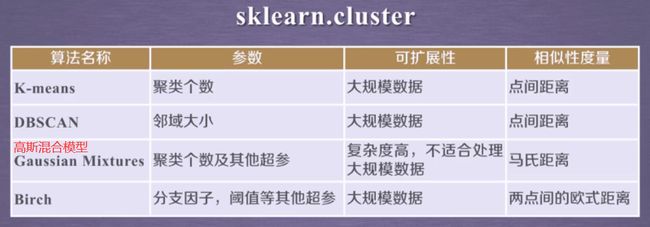
~Sklearn vs. 聚类：scikit-learn库(简称sklearn库)提供的常用聚类算法函数包含再sklearn.cluster这个模块中，如：K-Means，近邻传播算法，DBSCAN，等。

以同样的数据集应用于不同的算法，可能会得到不同的结果，算法所耗费的事件也不尽相同，这是由算法的特性决定的。

下图是调用sklearn库的标准函数对不同数据集执行的聚类结果

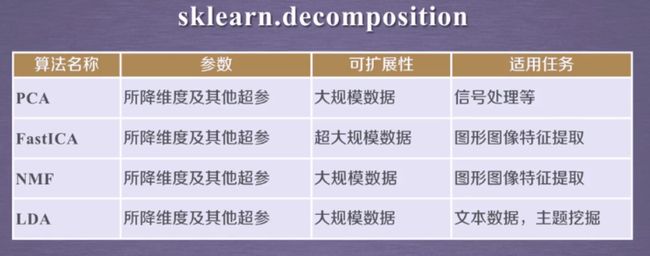
降维：降维就是再保证数据所具有的代表性特性或者分布的情况下，将高维数据转化为地位数据的过程。

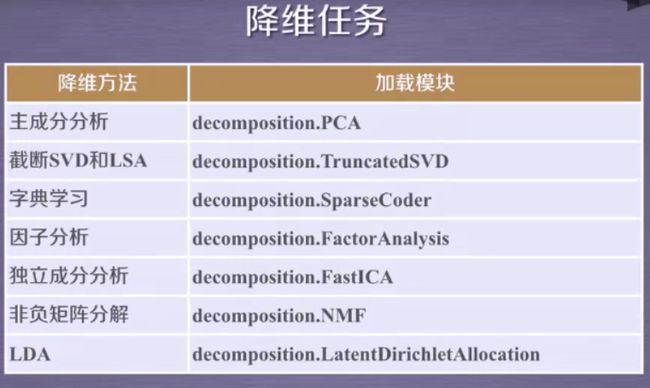
降维算法：sklearn库提供7种降维算法，降维过程可以理解为对数据集的组成成分进行分解（decomposition）的过程，因此sklearn为降维模块命名为decomposition，在对降维算法调用需要使用sklearn.decomposition模块。

强化学习（Reinforcement Learning，增强学习）： 通过观察，来学习执行什么样的动作，获得最好的回报，每个动作都会对环境有所影响，学习对象根据观察到的周围的环境的反馈来做出判断。

半监督学习（Semi-supervised Learning）：介于监督学习和无监督学习之间的一类学习方法

深度学习（Deep Learning）：利用深层神经网络模型，抽象数据的表示特征的一种方法。

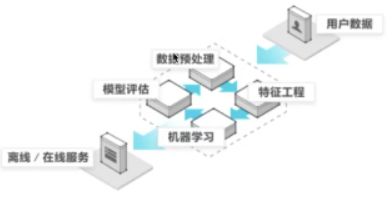
3.机器学习开发流程

1）获取数据

2）数据处理

3）特征工程

4）机器学习算法进行训练 — 模型

5）模型评估

流程图：

4.学习框架和资料介绍

机器学习库和框架：

深度学习框架：Scikit-Learn（传统的机器学习算法），TensorFlow （Google），pytorch（FaceBook），Caf fe2（FaceBook），theano（TensorFlow前身），Chainer（pytorch前身）

书籍资料推荐：

机器学习 —”西瓜书“ 周志华

统计学习方法 — 李航

深度学习 —”花书“

视频课程推荐：

前百度首席科学家，斯坦福教授，在线教育平台Coursera的联合创始人吴恩达录制的在线机器学习课程

斯坦福大学的《CS231N》课程主要介绍深度学习在计算机视觉领域的应用

AlphaGo的主要开发者，GOOGLE DeepMind的团队的David Silver珠江的有关强化学习，深度强化学习的原理及其应用技术的课程

5.数据集

可用数据集源：

sklearn

kaggle（https://www.kaggle.com/datasets）

UCI（https://archive.ics.uci.edu/ml/index.php）

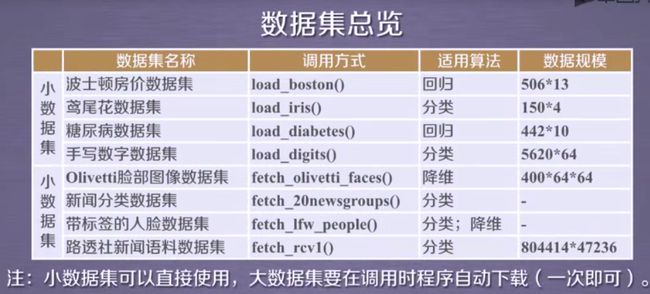
Scikit-Learn包含的常用数据集：

Scikit- Learn工具介绍

安装依赖库：Numpy，scipy，joblib

安装方法：pip install sklearn

Scikit-Learn包含的内容

scikit-learn数据集API介绍

sklearn.datasets

(*代表某个数据集的名字)

datasets.load_*() ——> 获取小规模数据集，数据包含在datasets里

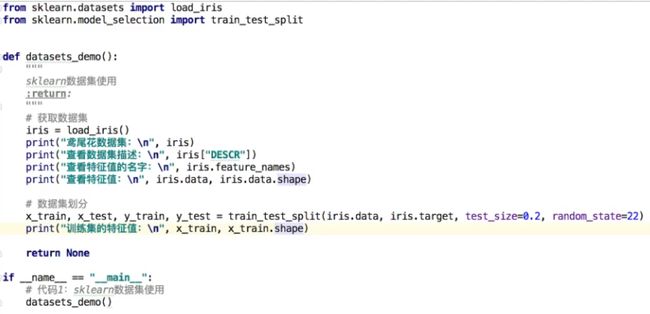
获取小数据集示例：

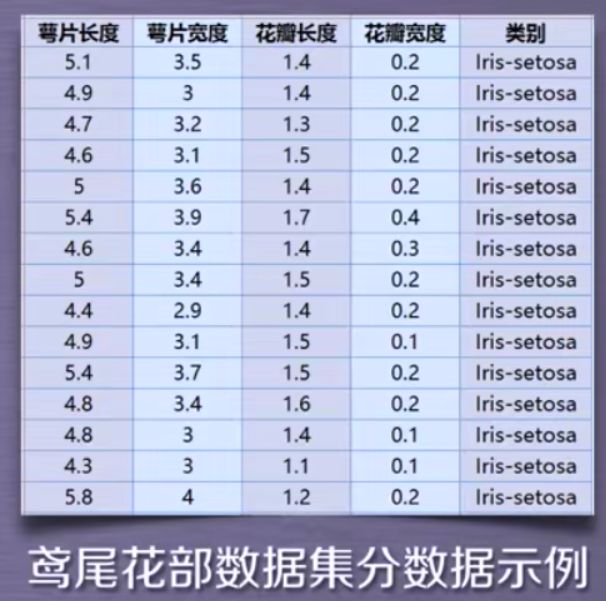
sklearn.datasets.load_iris()

加载并返回鸢尾花数据集，鸢尾花数据集采集的是鸢尾花的测量数据以及其所属的类别。测量数据包括：萼片长度、萼片宽度、花瓣长度、花瓣宽度。

类别共分为三类：Iris Setosa，Iris Versocolour，Iris Virginica。该数据集可用于多分类问题。

名称	数量
类别	3
特征	4
样本数量	150
每个类别 数据	50

sklearn.datasets.load_boston()

可选参数：return_X_y，默认为False，表示以字典形式返回数据全部信息（包括data和target）；若为True，则以（data,target）形式返回数据。

加载并返回波士顿房价数据集，波士顿数据集包含506组数据，每条数据包含房屋以及房屋周围的详细信息。其中包括城镇犯罪率、一氧化氮浓度、住宅平均房间数、到中心区域的加权平均距离以及自住房平均房价等。因此，波士顿房价数据集能够应用到回归问题上。

名称	数量
目标类别	5-50
特征	13
样本数量	506

datasets.fetch_*(data_home=None) ——>获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录，默认是 ~/scikit_learn_data/

获取大规模数据集示例：

sklearn.datasets.fetch_20newsgroups(data_home=None,subset=“train”)

subset：“train"或者"test”，“all”，可选，选择要加载的数据集

训练集的"训练"，测试机的"测试"，两者的"全部"

sklearn数据集返回值介绍

load和fetch返回的数据类型datasets.base.Bunch（字典格式：键值对）

data：特征数据数组（特征值），是（n_samples*n_features）的二维numpy.ndarray数组。

target：标签数组（目标值）， 是n_samples的一维numpy.ndarray数组

DESCR：数据描述

feature_names：特征名

target_names：标签名

data.base.Bunch（继承自字典）

dict[“key”] = value

dict.key = value

6.数据集的划分

训练数据：用于训练、构建模型

测试数据：在模型检测时使用，用于评估模型是否有效

测试集：20%~30%个样本

API：sklearn.model_selection.train_test_split(*arrays,*options)

参数：

x 数据集的特征值

y 数据集的目标值

test_size 测试集的大小，一般为float，如果为0.2，则训练集有80%，测试集有20%，test_size默认在20%-30%

random_state 随机数种子，不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。

返回值：

训练集特征值（通常用x_train来接受返回值），测试集特征值（x_test），训练集目标值（y_train），测试集目标值（y_test）

demo：

7.特征工程

定义：是使用专业背景知识和技巧处理数据，使得特征技能在机器学习算法上发挥更好的作业的过程。

意义：会直接影响机器学习的效果

工具：sklearn 特征工程 pandas 数据清洗、数据处理

特征抽取/特征提取：

定义：将任意数据（如文本或图像）转换为可用于机器学习的数字特征，也叫特征值化

特征提取API：sklearn.feature_extraction

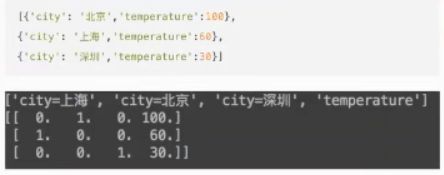
字典特征提取

sklearn.feature_extraction.DictVectorizer(sparse=True…)

vector 数学：向量 物理：矢量

矩阵 matrix 二维数组

向量 vector 一维数组

父类：转换器类

DictVectorizer.fit_transform(X) X：字典或包含字典的迭代器返回值：返回 sparse（稀疏） 矩阵

DictVectorizer.get_feature_names() 返回特征名称

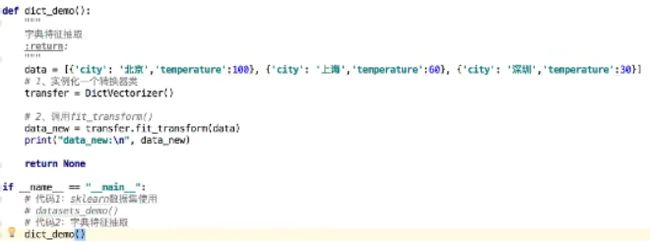
demo：

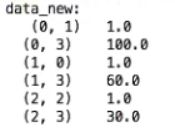
运行结果（sparse矩阵）：

区别：不显示0，节省内存，提高加载效率

当实例化DictVectorizer时，默认sparse=True，设为False后，运行结果如下：

区别：显示0

文本特征提取

单词 作为 特征

特征：特征词

方法1：统计每一个文档中的特征词出现的个数

sklearn.feature_extraction.text.CountVectorizer(stop_words=[])

stop_words 停用词—>停用词表 将停用词添加到列表中，则不统计停用词出现频率

CountVectorizer.fit_transform(X) X：文本或者包含文本字符窜的可迭代对象 返回值：返回sparse词频矩阵

from sklearn.feature_extraction.text import CountVectorizer


def count_demo():
    """
    文本特征提取：CountVectorizer
    :return:
    """
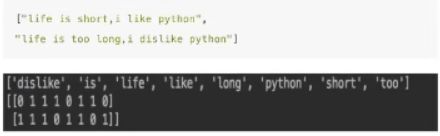
    data = ['life is short, i like like python', 'life is too long i dislike python']
    # 实例化一个转换器类
    transfer = CountVectorizer()
    # 调用fit_transform
    data_new = transfer.fit_transform(data)
    # data_new默认为sparse矩阵，CountVectorizer不支持内部参数sparse，如果要返回一个二维矩阵，调用sparse内toarray方法
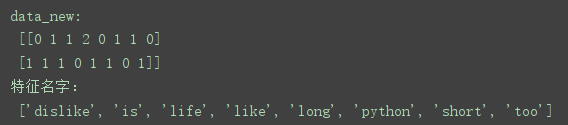
    print("data_new:\n", data_new.toarray())
    print("特征名字：", transfer.get_feature_names())

    return None


if __name__ == '__main__':
    count_demo()

结果：

如果将上面的英文替换为中文，则需要将词与词之间加上一个空格，否则将视短语为单词，统计出现频率。

如何自动地为词与词之间加上空格？需要使用python第三方库 jieba

from sklearn.feature_extraction.text import CountVectorizer
import jieba


def cut_word(text):
    """
    进行中文分词："我爱北京天安门" ——>"我 爱 北京 天安门"
    :param text:
    :return:
    """
    # jieba.cut()方法返回一个生成器对象，将生成器对象强制转换为列表，然后用join方法转换为以空格分隔的字符串。
    return " ".join(list(jieba.cut(text)))


def count_chinese_demo2():
    """
    中文文本特征提取，自动分词
    :return:
    """
    # 要进行特征工程的文本数据
    data = ['奈何桥上最后一次回眸，把对红尘的最后一丝留恋化成那苍白双颊的两行清泪。泪入孟婆汤，驻首三生石，千世的冰封，万年的孤寂，那一刻全部回归于寂静。奈何前世的离别，奈何今生的相见。浮生若梦，百折千回。',
            '后悔是一种耗费精神的情绪，后悔是比损失更大的损失，比错误更大的错误，所以不要后悔。',
            '我最信任的人，用背叛，教会了我不要轻易相信任何人。世界上最远的距离，不是爱，不是恨，而是熟悉的人，渐渐变得陌生。']
    data_new = []
    for x in data:
        # 将分词后的中文文本添加到列表中
        data_new.append(cut_word(x))
    # 实例化一个转换器类，设置无意义的停用词
    transfer = CountVectorizer(stop_words=["不是", "不要", "一次", "一丝"])
    # 调用fit_transform得到一个sparse矩阵
    data_final = transfer.fit_transform(data_new)
    # 将sparse矩阵转换为一个二维数组并打印
    print("data_new：\n", data_final.toarray())
    print("特征词：\n", transfer.get_feature_names())
    return None


if __name__ == '__main__':
    count_chinese_demo2()

结果：（部分）

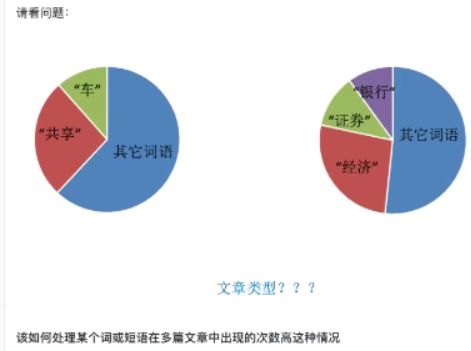
关键词：在某一个类别的文章中，出现的次数很多，但是在其他类别的文章中出现很少。

问题：

方法2：计算tf-idf这样的指标，找到一篇文章中的词的重要程度，有利于文章的分类。

Tf-idf文本特征提取（机器学习中进行文章分类经常用到TF-IDF）

TF-IDF的主要思想是：如果某一个词或短语在一篇文章中出现的概率高，并且在其它文章中很少出现。则认为此词或者短语具有很好的类别区分能力，适合用来分类。

TF-IDF作用：用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。

TF —> 词频（term（词语、术语） frequency（频率），tf），即指的是某一个给定的词语在该文件中出现的频率。

IDF —> 逆向文档频率（inverse（反向的） document frequency，idf），即是一个词语普遍重要性的度量，某一个特定词语的idf，可以由总文件数目除以包含该词语之文件的数目，再将得到的商除以10为底的对数得到。

举例：

假设一个语料库含有1000篇文章，出现关键字”非常“的文章有100篇，出现关键字”经济“的文章有10篇，在文章A中含有100个词语，其中出现了10次”经济“，在文章B中含有100个词语，其中出现了10次”非常“，求文章A和文章B的tf、idf。

A：tf = 10/100 = 0.1 idf = log 10 1000/10 = 2 TF-IDF = 0.1 * 2 = 0.2

B：tf = 10/100 = 0.1 idf = log 10 1000/100 = 1 TF-IDF = 0.1 * 1 = 0.1

对数？

2 * 3 = 8

log 2 8 = 3

求tf-idf的公式：

最终求出的结果（TF-IDF）可以理解为重要程度。

如何在sklearn中使用TF-IDF？

API：sklearn.feature_extraction.text.TfidfVectorizer(stop_words=None…)

返回词的权重矩阵

TfidfVectorizer.fit_transform(X) X：文本或者包含文本字符串的可迭代对象

返回值：返回sparse矩阵

调用sparse类的toarray方法返回二维数组

将上面使用CountVectorizer进行文本特征提取的代码中的转换器类改为TfidfVectorizer即可

权重大的词表示重要程度高，该词更具有分类意义

图像特征提取

暂无学习

特征预处理

定义：通过一些转换函数将特征数据转换成更加适合算法模型的特征数据的过程

包含内容：数值型数据的无量纲化 方法：1.归一化 2.标准化

特征处理API：sklearn.preprocessing

为什么要进行归一化/标准化？

特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征

无量纲化（即希望不同规格的数据转换为同一规格），之所以进行无量纲化就是因为量纲不统一，导致里程数的数值会非常大，而消耗时间比的数组非常小，为了让特征同等重要，所以要进行归一化/标准化，数学上叫做无量纲化。

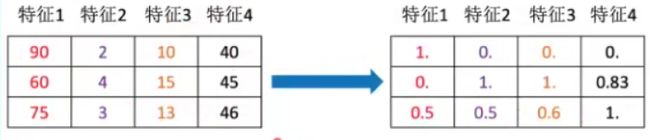
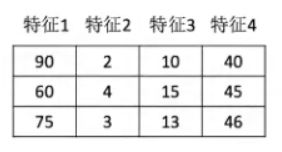
举例：下面有三个特征值分别是 里程数、公升数、消耗时间比，后两者因为数值较小，所以对最终的结果基本没有影响，为了使得这三个特征值同等重要，所以要进行归一化/标准化

归一化：

定义：对原始的数据进行变换把数据映射到（默认为[0,1]）之间

公式：

数据：

计算特征1值为90的归一化值：x’ = (90-60)/(90-60) = 1 x’’ = 1 * (1 - 0) + 0 = 1 即归一化值x’’=1。

如何在sklearn中使用归一化方法？

API：sklearn.preprocessing.MinMaxScaler(feature_range=(0,1)…)

MinMax：因为归一化是根据最大值和最小值求出来的；Scaler：放缩器

MinMaxScaler：按照最小值、最大值来进行放缩，放缩范围就是feature_range，默认为0-1。

feature_range=(,)：归一化的范围

MinMaxScaler.fit_transform(X) X：numpy.array格式的数据[n_samples, n_feature] —> 二维数组，行为样本，即（有几个样本就有几行），列为特征，即（有几个特征就有几列）。

返回值：转换后的形状相同的array（原先几行几列就返回相同行列的ndarray）

示例：

数据：

dating.txt

说明：（附件数据部分截图，包括里程数、公升数、消耗时间比和目标值），即上面的约会对象数据，由于每个特征下的数据差值参差不齐，所以对这些数据进行归一化处理，使得每个特征同等重要。

代码：

from sklearn.preprocessing import MinMaxScaler
import pandas as pd

def minmax_demo():
    """
    归一化
    :return:
    """
    # 1.获取数据
    data = pd.read_csv("dating.txt")
    data = data.iloc[:, :3]
    # 2.实例化一个转换器类
    transfer = MinMaxScaler(feature_range=(0,1))
    # 3.调用fit_transform()，进行归一化处理
    data_new = transfer.fit_transform(data)
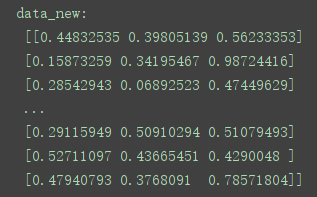
    print("data_new:\n", data_new)

    return None
    

if __name__ == '__main__':
    minmax_demo()

结果：

总结：归一化使得原始数据映射到一个固定范围的区间内，这样使得每个特征同等重要。

缺点：

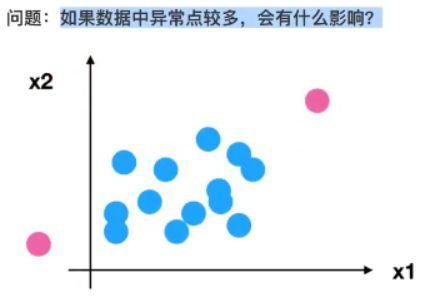
归一化的结果是根据最大值和最小值求出来的，如果最大值或者最小值异常，那么归一化的值也不会太准，所以这种方法鲁棒性（稳定性、健壮性）较差，只适合传统精确小数据场景。

解决这一问题（缺陷）的方法：

标准化：

定义：通过对原始数据进行变换把数据变换到均值为0，标准差为1范围内。

公式：

（原始数据减去这一列的平均值（mean），然后再除以标准差（σ））

标准差：衡量离散（集中）程度

对于归一化来说：如果出现异常点，影响到了最大值和最小值，那么结果显然会发生改变

对于标准化来说：如果出现异常点，由于具有一定数据量，小量的异常点对于平均值和标准差的影响并不大，所以标准化比较稳定。

如何在sklearn中使用标准化方法？

API：sklearn.preprocessing.StandardScaler()

处理之后，对每列来说，所有的数据都聚集在均值为0附近，标准差为1。

StandardScaler.fit_transform(X) X：numpy.array格式的数据[n_sample, n_features]

返回值：转换后的形状相同的array

示例：

代码如上归一化代码，使用同样的数据集，导入StandardScaler，改变转化器类。

结果：

总结：对数据进行无量纲化处理一般选择使用标准化方法

应用场景：在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

特征降维

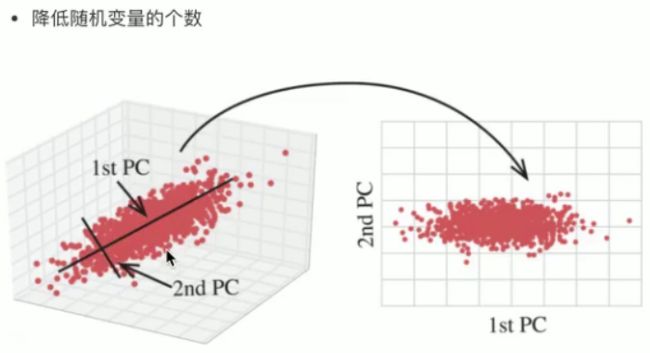
定义：降维是指在某些限定条件下，降低随机变量（特征）个数，得到**一组“不相关”**主变量的过程

特征降维要求特征与特征之间不相关

相关特征：

相对湿度与降雨量之间的相关

降维的两种方法：

1）特征选择

定义：数据中包含冗余或者相关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

特征选择API：sklearn.feature_selection

比如：如果下图特征中有 是否有爪子 这一项特征，所有的鸟基本上都有这一特征，那么这个特征就是冗余数据。

特征选择的两种方法：

Filter过滤式：

低方差特征过滤：如果一组特征方差比较小，说明特征值接近（即该特征为冗余数据，没有意义），那么选择过滤掉这组特征。

API：sklearn.feature_selection.VarianceThreshold(threshold=0.0)

Variance—方差 Threshold—（阈值）起点值

threshold= 设置一个起点值，一组特征的方差如果低于这个起点值，就删掉，默认方差为0

Variance.fit_transform(X) X：numpy.array格式的数据[n_samples, n_features]

返回值：训练集方差低于threshold的特征将被删除，默认值是保留所有非零方差特征，即删除所有样本具有相同值的特征。

示例：

数据：对某些股票的指标特征之间进行一个筛选，除去"index"、“date”、"return"列不考虑（不是所需要指标）
附件：
百度网盘 提取码：love
附件部分截图：

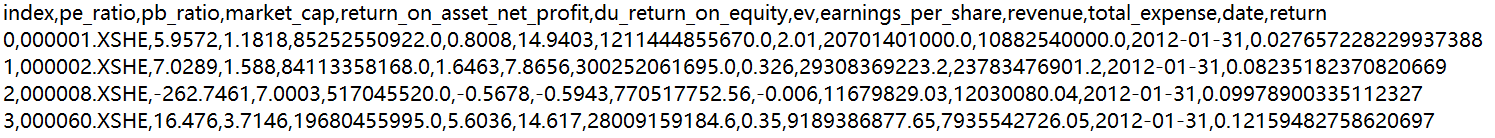
总共9个特征（不包括index、date、return）

代码：

from sklearn.feature_selection import  VarianceThreshold
import pandas as pd

def variance_demo():
    """
    低方差特征过滤
    :return:
    """
    # 1.获取数据
    data = pd.read_csv("factor_returns.csv")
    # 去掉"index"、"date"、"return"列
    data = data.iloc[:, 1:-2]
    # 2.实例化一个转换器类，设置方差阈值为10，方差低于这个值的特征将被删除
    transfer = VarianceThreshold(threshold=10)
    # 3.调用fit_transform()
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new, data_new.shape)

    return None
    
if __name__ == '__main__':
    variance_demo()

结果：

可以看到，特征数量由原来的9个变为7个，即低于方差阈值的两个特征被删除。
相关系数：特征与特征之间的相关程度

皮尔逊相关系数（Pearson Correlation Coefficient）：反映变量之间相关关系密切程度的统计指标

Correlation—相关 Coefficient—系数

公式：

皮尔逊相关系数计算过程：

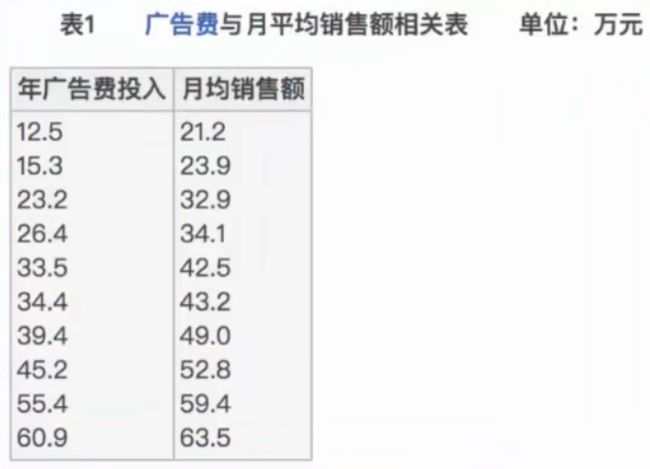
比如说，计算年广告费投入与月平均销售额

那么之间的相关系数怎么计算？

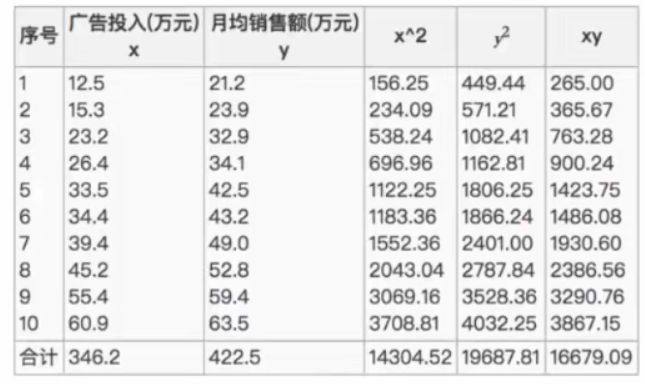
n代表样本数量，设广告投入为x，月均销售额为y，求出x乘y的加和，x的加和、y的加和、x平方的加和y平方的加和

代入上述皮尔逊公式，最终计算出相关系数（r）的结果：

那么相关系数的值代表什么意义？

相关系数的值介于-1与+1之间，即-1≤r≤+1。其性质如下：

当r>0时，表示两变量正相关，r<0时，两变量负相关

当|r|=1时，表示两变量为完全相关，当r=0时，表示两变量间无相关关系

当0<|r|<1，表示两变量存在一定程度的相关，且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性关系越弱

一般可按三级划分：|r|<0.4为低度相关，0.4≤|r|<0.7为显著性相关；0.7≤|r|<1为高度线性相关

所以上述计算的结果表明，广告投入费与月平均销售额具有高度的正相关关系。

如何去使用皮尔逊相关系数来计算？

API：scipy.stats.pearsonr(x, y)

x：(N,) array_like

y：(N,) array_like

返回值：(Pearson’s correlation coefficient, p-value)

示例：

对之前进行过特征选择的股票案例进行财务指标相关性计算。

代码：

from scipy.stats import pearsonr
import pandas as pd


def pearsonr_demo():
    """
    皮尔逊相关系数计算
    :return: 
    """
    # 1.获取数据
    data = pd.read_csv("factor_returns.csv")
    data = data.iloc[:, 1:-2]
    # 2.对股票的相关指标进行皮尔逊相关系数计算,得到相关系数值
    r1 = pearsonr(data['pe_ratio'], data['pb_ratio'])
    print("pe_ratio和pb_ratio之间的相关性：\n", r1)
    r2 = pearsonr(data['revenue'], data['total_expense'])
    print("revenue和total_expense之间的相关性：\n", r2)
    
if __name__ == '__main__':
    pearsonr_demo()

结果：

特征与特征之间相关性很高：

1）选取其中一个

2）加权求和

3）主成分分析：自动将相关性很强的特征处理掉

Embeded嵌入式：

决策树：

正则化：

深度学习：

2）主成分分析（PCA）

定义：将高维数据转化为低维数据，在此过程中可能会舍弃原有数据，创造新的变量。

作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。

应用：回归分析或者聚类分析当中

如何用相机最好的对一个立体的物体二维表示（将三维降到二维），主成分分析就是尽可能的减少降维时数据的损失，第四张图片最能看出一个物体的信息。

（PCA的公式、计算过程暂不了解）

API：sklearn.decomposition.PCA(n_components=None)

decomposition—分解（降维）

P—principal—主要的 C—component—成分 A—analysis—分析

将数据分解为较低维数空间

n_components：

小数：表示保留百分之多少的信息

整数：减少到多少特征（如果将三维的数据降到二维，那么n_components=2）

PCA.fit_transform(X) X:要进行降维处理的数据，numpy array格式[n_samples, n_fearures]

返回值：转换后指定维度的array

示例1：

数据：[[2, 8, 4, 5], [6, 3, 8, 8], [5, 4, 9, 1]] 三行四列，四个特征

代码：

from sklearn.decomposition import PCA


def pca_demo():
    """
    PCA降维
    :return:
    """
    data = [[2, 8, 4, 5], [6, 3, 8, 8], [5, 4, 9, 1]]
    # 1.实例化一个转换器类，指定n_components=3（整数），即降到3个特征，指定n_components=0.95（小数），则保留95%的特征
    transfer1 = PCA(n_components=3)
    transfer2 = PCA(n_components=0.95)
    # 2.调用fit_transform
    data_new1 = transfer1.fit_transform(data)
    data_new2 = transfer2.fit_transform(data)
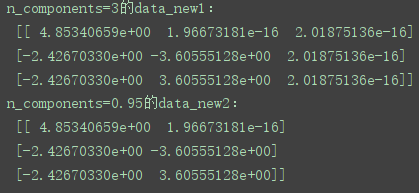
    print("n_composition=3的data_new1：\n", data_new1)
    print("n_composition=0.95的data_new2：\n", data_new2)
    return None
    
if __name__ == '__main__':
    pca_demo()

结果：

示例2：探究用户对物品类别的喜好细分降维（Kaggle上的一个比赛）

数据：instacart

链接：https://pan.baidu.com/s/1xeMaS9b8-A9cWI_McF8-zw

提取码：love

aisle—过道，英语中用过道来代表一个个商品的类别

aisles.csv：商品所属具体物品类别
字段：

aisle_id	aisle

order_products_prior.csv：订单与商品信息
字段：

order_id	product_id	add_to_cart_order	reordered

orders.csv：用户的订单信息
字段：

order_id	user_id	eval_set	order_number	order_dow	order_hour_of_day	days_since_prior_order

products.csv：商品信息
字段：

product_id	product_name	aisle_id	department_id

通过对表的分析，发现用户ID（user_id）在orders.csv文件中，而物品种类（aisle）在aisles.csv文件中，只有通过发现表与表中的共同键并且一步步关联合并表，才能使得user_id和aisle出现在同一张表中，从而分析出用户对不同物品种类的喜好。

# 总体思路
# 1.获取数据
# 2.合并表
# 3.找到user_id和aisle之间的关系
# 4.pca降维

import pandas as pd
# 1.获取数据
order_products = pd.read_csv("instacart/order_products__prior.csv")
products = pd.read_csv("instacart/products.csv")
orders = pd.read_csv("instacart/orders.csv")
aisles = pd.read_csv("instacart/aisles.csv")

# 2.合并表
# 合并aisles和products，aisle和product_id就关联了
tab1 = pd.merge(aisles, products, on=["aisle_id", "aisle_id"])

# 合并tab1和order_products，aisle和order_id就关联了
tab2 = pd.merge(tab1, order_products, on=["product_id", "product_id"])

# 合并tab2和orders，aisle和user_id就关联了
tab3 = pd.merge(tab2, orders, on=["order_id", "order_id"])

# 3.找到user_id和aisle之间的关系
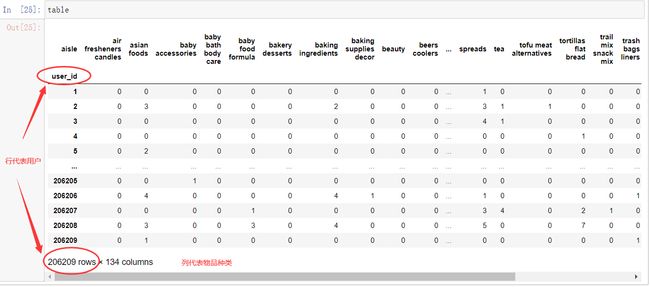
table = pd.crosstab(tab3["user_id"], tab3["aisle"])

table的结果如下：0代表没有购买，会发现有大量的冗余数据，因此要进行特征降维

# 由于数据量特别大，这里只处理一万条用户的数据
data = table[:10000]
# 4.PCA降维
from sklearn.decomposition import PCA
# 1）实例化一个转换器类
transfer = PCA(n_components=0.95)
# 2）调用fit_transorm
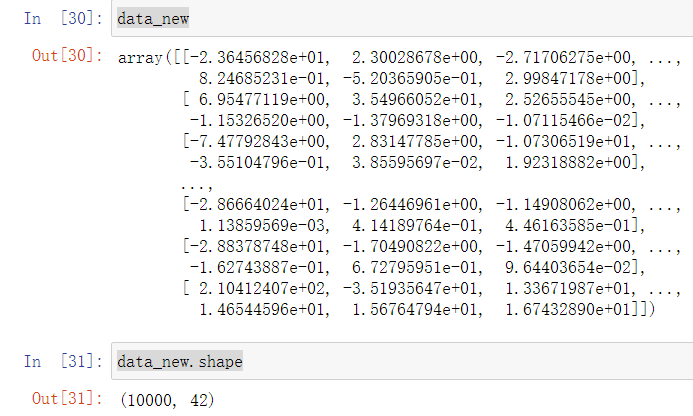
data_new = transfer.fit_transform(data)

结果：

可以看到，物品种类由之前的134个降到了42个，而且保留了95%的信息。

学习大纲：

关于jupyter可能出现的问题：

jupyter运行后显示空白的问题解决：

卸载之前的jupyter notebook：pip uninstall jupyter-core（注意卸载的是jupyter-core）

然后重新安装：pip install jupyter

安装过程中出现这个错误：

ERROR: notebook 6.0.3 has requirement tornado>=5.0, but you’ll have tornado 4.5.3 which is incompatible.

说明jupyter notebook 6.0.3必须要求tornado版本>=5.0，版本之间的不兼容导致出现运行jupyter不显示文件的问题

重装tornado即可：pip install tornado

ERROR: pyspider 0.3.10 has requirement tornado<=4.5.3,>=3.2, but you’ll have tornado 6.0.4 which is incompatible.

安装完tornado后，又出现pyspider0.3.10必须要求3.2

。。。pyspider截止到20200716最新版本为0.3.10没有更新，如果要用只好建虚拟环境了安装tornado和pyspider的对应版本。

jupyter默认打开文件路径的更改方法：

在家目录下找到.jupyter，看看里面是否有jupyter_notebook_config.py

如果没有，打开cmd，输入jupyter notebook --generate-config生成这个配置文件，然后打开文件，修改c.NotebookApp.notebook_dir = ‘’，去掉前面的#，单引号内输入想要默认打开的文件路径

如：

保存后，重新启动jupyter notebook即可。