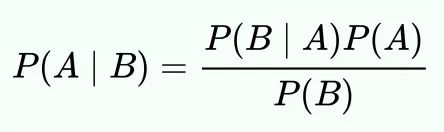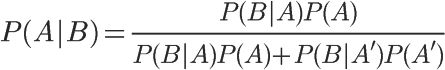(以下文章部分内容来自于孤独大脑公众号的阅读体会)
贝叶斯公式想要阐述的意义是:新信息出现后, A事件的概率=A事件本身的概率 x 新信息带来的调整。简而言之, 就是看到新的证据后, 更新想法。
"新信息"在贝叶斯公式中, 代表著"已知条件"。见下图:
公式看起来稍微有点复杂, 不过不要害怕, 以下我们将一一来做拆解:
- P(A|B)= 已知B发生后, A发生的条件概率, 也可称为A的"后验概率"(新信息B出现后, A发生的概率也会有所调整; 后验概率指的是在得到某部分"结果"信息后, 重新修正的概率)
- P(B|A)= 已知A发生后, B发生的条件概率
- P(A)= A的先验概率, "先验"概率指的是不考虑其他信息或条件(ex. B) 下, A发生的概率
- P(B)= B的先验概率
可以再拓展一下:
- P(B|A')= 已知非A, B发生的条件概率
- P(A)= 非A的先验概率
以一个比较经典的例子来展示计算过程:
- P(a)=被检测者患病的概率=0.1%
- P(a')=被检测未者患病的概率=99.9%
- P(b|a)=已知患病的情况下检测为阳性的概率=99%
- P(b|a')=已知未患病的情况下检测为阳性的概率=1%
现在, 从人群中随机抽一个人去检测,医院给出的检测结果为阳性,那么这个人实际得病的概率是多少?
我们要算的是P(a|b)=0.990.001/(0.990.001+0.01*0.999)=9%
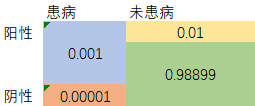
用可视化的面积展示看起来会更直观一些:
从上图可知, 蓝色的面积/(蓝色+黄色+绿色中属于阳性)的面积, 就是我们要的答案。
贝叶斯定理本质上是一个很简单的规则:
当你收到新的论据(B)时, 它会用来改变你对某个假设的信任度。
--如果论据和假设一致, 则假设成立的概率上升
--反之则下降
你首先赋予某个事件一个"先验概率", 然后通过新证据来修正, 得到一个"后验概率", 然后把这个"后验概率"变成新的"先验概率", 再做一次修正, 如此循环往复......
这也就是机器学习训练模型的最朴实的基础算法。神经网络最重要的用途是分类; 分类器的输入是一个数值向量,作为类的特征。
我们把搜集到的数值向量做分区, 并且画出一条分界线, 以后新的向量进来, 可以直接区分到底是A还是A' 。而所谓的神经元, 就是一个分类器: 一个n-1维超平面把n维空间一分为二,两边分属不同的两类。
一份数据经过神经元大刀一挥, 就可把类型一分为二。即使是一个多维空间, 只要砍足够多刀, 也能够对一些复杂的函数和空间分布做出解释。
我们先选择一个判断条件, 可以是一条线/平面/超平面, 然后把样本一个个拿过来, 如果这条直线分错了, 说明这个点分错边了, 这时候我们可以动态挪一下判断的线, 让样本跑到直线正确的一侧。因此训练神经元的过程就是这条直线不断在跳舞,最终跳到两个类之间的竖直线位置。