栈、单调栈 题解合集
目录
栈的典型应用
(1)Leetcode第20题-有效的括号
(2)Leetcode第155题-最小栈
单调栈
(1)Leetcode_T496 下一个更大元素
(2)Leetcode_T456 132模式
(3)Leetcode_T503 下一个更大元素||
(4)Leetcode_T1118
(5)Leetcode_T739 每日温度
(6)Leetcode_T121 买卖股票的最佳时机
(7)Leetcode_T42 接雨水
(8)Leetcode_T84 柱状图中最大的矩形
栈的典型应用
(1)Leetcode第20题-有效的括号
20. 有效的括号 - 力扣(LeetCode) (leetcode-cn.com)
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
思路:
(1)如果字符串长度为奇数,直接返回false
(2)最开始左括号入栈,当遇到右括号时,判断:
(3)栈不为空并且栈顶左括号与这个右括号匹配,则栈顶左括号出栈
当栈为空或者栈顶元素与这个右括号不匹配,直接返回false
(4)可以遍历完,则返回true
【小细节】判断左右括号是否匹配,可以用哈希先预存对应关系,也可以根据相匹配的括号的ASCII的值相差为2
代码:
public boolean isValid(String s) {
// 如果字符串长度为奇数,必然匹配不够,返回false
int n = s.length();
if(n % 2 == 1){
return false;
}
// 用哈希表存储括号,便于比较
Map map = new HashMap(){{
put(')','(');
put('}','{');
put(']','[');
}};
Deque stack = new LinkedList();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if(map.containsKey(c)){
if(stack.isEmpty() || stack.peek() != map.get(c)){
return false;
}
stack.pop();
}
else{
stack.push(c);
}
}
return stack.isEmpty();
} (2)Leetcode第155题-最小栈
155. 最小栈 - 力扣(LeetCode) (leetcode-cn.com)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
思路:此题关键是检索栈中最小元素,这里我们用辅助栈,辅助栈与原栈同步进行
对于辅助栈s2,每push一个新元素x:
s2.push(Math.min(s2.peek(),x))
对于辅助栈s2,每pop一个新元素,s2也pop元素
代码:
public class MinStack {
Deque stack;
Deque minStack;
// 无参构造初始化
public MinStack() {
stack = new LinkedList<>();
minStack = new LinkedList<>();
minStack.push(Integer.MAX_VALUE);
}
// 入栈
public void push(int val) {
stack.push(val);
minStack.push(Math.min(minStack.peek(), val));
}
// 出栈
public void pop() {
stack.pop();
minStack.pop();
}
// 返回栈顶元素
public int top() {
return stack.peek();
}
// 返回最小值
public int getMin() {
return minStack.peek();
}
} 单调栈
单调栈——栈内元素要么按照单调递增顺序要么单调递减顺序
(1)Leetcode_T496 下一个更大元素
496. 下一个更大元素 I - 力扣(LeetCode) (leetcode-cn.com)
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素
整体思路:
遍历nums2,将nums2中每个元素对应的下一个更大元素存储到哈希表中
再遍历nums1,从哈希表中找到nums1各个元素对应的下一个更大元素即可
局部——如何找nums2中每个元素对应的下一个更大元素
维护一个单调递减栈,对于nums2,从后向前遍历,对于元素x,如果单调栈为空,说明没有比x更大的,直接返回 - 1,如果栈不为空,则依次比较x与栈顶元素大小,栈顶不是更大的就换下一个栈顶,直到找到更大的或者栈为空了
【注意】每次的x都要入栈,作为下一个元素比较之一
代码:
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
// 哈希表,用于存储nums2中元素与下一个更大元素的对应关系
Map map = new HashMap<>();
Deque stack = new LinkedList<>();
int n = nums2.length;
// 类似739题,但是是找nums2中元素的下一个更大元素
// 这里注意,从最后一个元素反着来,不然找不到类似3,1,4中3的下一个更大元素
for (int i = n - 1; i >= 0; i--) {
while (!stack.isEmpty() && nums2[i] >= stack.peek()) {
stack.pop();
}
map.put(nums2[i], stack.isEmpty() ? -1 : stack.peek());
stack.push(nums2[i]);
}
int res[] = new int[nums1.length];
// 从哈希表中找与nums1元素值相等的对应的元素
for (int i = 0; i < res.length; i++) {
res[i] = map.get(nums1[i]);
}
return res;
} (2)Leetcode_T456 132模式
456. 132 模式 - 力扣(LeetCode) (leetcode-cn.com)
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。
如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。
整体思路:对于3,要保证3大于1又小于2,同时,3又是最后一个元素,所以我们从这里入手
从右向左遍历,维护一个单调递减栈,元素入栈,当遇到比栈顶元素大的,说明可以构成互逆的32模式,现在只差找1了,我们先将栈内比2小的元素出栈,引入变量k,令k等于最大的3,也即出栈元素中最大的(因为3>1,所以尽可能找最大的3),接着入栈,当可以找到一个新入栈元素 < k时,说明可以找到1,返回true
代码:
class Solution {
public boolean find132pattern(int[] nums) {
int n = nums.length;
int m = Integer.MIN_VALUE;
Deque stack = new LinkedList<>();
// 从右向左遍历,维护一个单调递减栈,更小的直接入栈
for (int i = n - 1; i >= 0; i--) {
// 只要能遇到小于m的,说明存在1,符合132模式
if (nums[i] < m) return true;
// 当遇到大于栈顶的,说明遇到了一对2、3,将大于2的3全部出栈,并令m=最大的那个3
while (!stack.isEmpty() && stack.peek() < nums[i]) {
m = stack.pop();
}
stack.push(nums[i]);
}
return false;
}
} (3)Leetcode_T503 下一个更大元素||
503. 下一个更大元素 II - 力扣(LeetCode) (leetcode-cn.com)
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
思路:两个for循环暴力求解也是可以通过的,但因为时间复杂度为O(n^2),效率低
故而我们借助单调栈求解
单调栈存储的是元素索引下标,因为是循环数组,所以for循环从 0--2*长度-1,通过模n运算,达到循环遍历的目的。
【注意】目标数组一开始赋初值为-1,再借助单调栈,遇到比栈顶元素大的,说明遇到了下一个更大元素,将栈内元素出栈并在目标数组中更新这些元素的下一个更大元素
//下一个更大元素||
public class Leetcode_T503 {
// 单调栈存储下标
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] res = new int[n];
// 默认为 -1
Arrays.fill(res, -1);
Deque stack = new LinkedList<>();
int count = 2 * n - 1;
for (int i = 0; i < count; i++) {
while (!stack.isEmpty() && nums[stack.peek()] < nums[i % n]) {
res[stack.pop()] = nums[i % n];
}
stack.push(i % n);
}
return res;
}
}
// 自己的本能解法:两个for循环遍历,暴力求解
// public int[] nextGreaterElements(int[] nums) {
// int n = nums.length;
// int[] res = new int[n];
// if(n == 1){
// res[0] = -1;
// return res;
// }
// for (int i = 0; i < n; i++) {
// for (int count = 0; count < n; count++) {
// if(nums[(i + count) % n] > nums[i]){
// res[i] = nums[(i + count) % n];
// break;
// }else{
// res[i] = -1;
// }
// }
// }
// return res;
// }
//} (4)Leetcode_T1118
OMG 这道题是会员题。。。。。QAQ
(5)Leetcode_T739 每日温度
739. 每日温度 - 力扣(LeetCode) (leetcode-cn.com)
请根据每日 气温 列表 temperatures ,请计算在每一天需要等几天才会有更高的温度。如果气温在这之后都不会升高,请在该位置用 0 来代替。
整体思路:维护一个单调递减栈,当遇到温度比栈顶温度高的,说明已找到栈顶元素的下一个更高温度,并让栈顶出栈,这里,因为是单调递减栈,所以用while结构,不断出栈,直到保持递减
局部:因为问的不是下一个更高温度,而是几天后,所以我们可以让栈中存储元素索引下标,下标之差即为天数之差
public int[] dailyTemperatures(int[] temperatures) {
int[] ans = new int[temperatures.length];
// 单调栈记录温度的索引下标
Deque stack = new LinkedList<>();
int n = temperatures.length;
for (int i = 0; i < n; i++) {
// 栈不为空并且当前索引温度大于栈顶索引的温度时,记录栈顶索引的等待天数并将其出栈
while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
int index = stack.pop();
ans[index] = i - index;
}
// 栈为空或者当前温度小于等于栈顶索引温度时,将当前索引入栈
stack.push(i);
}
return ans;
} (6)Leetcode_T121 买卖股票的最佳时机
121. 买卖股票的最佳时机 - 力扣(LeetCode) (leetcode-cn.com)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
思路:
方法一:两个for循环暴力求解
方法二:单调栈
维护一个单调栈,当遇到比栈顶小的,令栈顶出栈,最新的小元素入栈
当遇到比栈顶大的,更新利润值(栈顶保持是目前遍历到的最小,相当于在栈顶那天买入)
方法三:动态规划
类似于单调栈的思路,也是一步步更新最小值,以确定最大利益
dp[i]表示截止到第i天的最低价格,dp[i] = Math.min(dp[i - 1] , price[i])
res是利润,res = Math.max(res , price[i] - dp[i])
代码:
public int maxProfit(int[] prices) {
Deque stack = new LinkedList<>();
int n = prices.length;
int max = 0;
stack.push(prices[0]);
for (int i = 1; i < n; i++) {
if (prices[i] < stack.peek()) {
int m = stack.pop();
stack.push(prices[i]);
} else {
max = Math.max(max, prices[i] - stack.peek());
}
}
return max;
}
//动规解法
//public int maxProfit(int[] prices) {
// int n = prices.length;
// int res = 0;
// int[]dp = new int[n];
// dp[0] = prices[0];
// for(int i = 1; i < n; i++){
// dp[i] = Math.min(dp[i - 1],prices[i]);
// res = Math.max(res, prices[i] - dp[i]);
// }
// return res;
//
//} (7)Leetcode_T42 接雨水
42. 接雨水 - 力扣(LeetCode) (leetcode-cn.com)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
思路:这道题解法也有多种,诸如动规、双指针,当然也可以使用单调栈,这里,我们主要讲单调栈的解法
整体思路:
维护一个单调递减栈,当栈内元素个数大于等于2并且新入栈元素大于栈顶时,形成一个低洼,这里可以接到雨水
求低洼处雨水面积:
- 待处理的低洼处我们用变量cur表示,cur = stack.pop()
- 当cur出栈后,新的栈顶即是低洼的左边界,用left表示,left = stack.peek()
- 右边界即为新遇到的这个较大的元素
- 雨水面积 = 底长 * 高度,对于底长,是right - left - 1(我们单调栈中存储索引下标),之于高度,是左右边界较低的高度再减去底座高度(底座高度就是cur的高度)
【注意】因为在计算高度时会减去底座高度,所以即使遇到平地型低洼,如2 1 1 2,我们的算法也依然正确,在cur=右边的1时,左边界为1,高度会减为0,所以并没有重复计算面积,只有cur=左边的1时,才会计算这处低洼的面积
代码实现:
public int trap(int[] height) {
int n = height.length;
int res = 0;
Deque stack = new LinkedList<>();
for (int i = 0; i < n; i++) {
while(!stack.isEmpty() && height[i] > height[stack.peek()]){
int cur = stack.pop();
// 栈内元素至少为2个才能和大的元素构成雨水区域,否则是边界,跳出while
if(stack.isEmpty()){
break;
}
int left = stack.peek();
int right = i;
// 宽度由左右边界相减得来
int width = right - left - 1;
// 这里注意,高度是左右俩边界较低的那个,再减去底座高度
// 所以不必担心平地的情况,譬如2 1 1 2,右边那个1的左边界为1,计算高度时会减为0,只要cur为左边的1时,左边界为2,高度为1
int high = Math.min(height[left],height[right]) - height[cur];
res += width * high;
}
stack.push(i);
}
return res;
} (8)Leetcode_T84 柱状图中最大的矩形
84. 柱状图中最大的矩形 - 力扣(LeetCode) (leetcode-cn.com)
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积
示例 1:
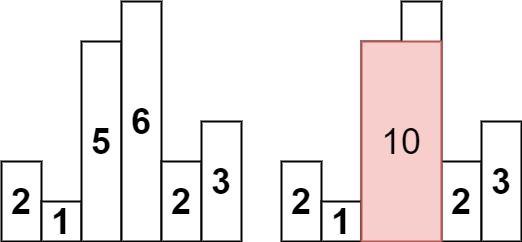
输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
思路:与接雨水差不多,都是求面积,但是这里,我们维护一个单调递增栈,当遇到小于栈顶的元素时,令cur = stack.pop() ,然后找以cur为高度的矩形的最大面积,同样是找左右边界以求宽,所以栈内存储的仍是索引下标
class Solution {
public int largestRectangleArea(int[] heights) {
int ret = 0;
Deque stack = new ArrayDeque<>();
int length = heights.length;
int[] h = new int[length + 2];
// 在高度数组左右加0作为边界
for (int i = 0; i < length; i++) {
h[i + 1] = heights[i];
}
for (int i = 0; i < length + 2; i++) {
// 当新入栈元素小于栈顶时,出栈并计算该栈顶元素能组成的最大矩形
while (!stack.isEmpty() && h[stack.peek()] > h[i]) {
int cur = stack.pop();
// 左边界
int left = stack.peek();
// 右边界
int right = i;
ret = Math.max(ret, (right - left - 1) * h[cur]);
}
// 栈中存储的实际是元素索引下标,为了计算左右边界(宽)
stack.push(i);
}
return ret;
}
}