GraphEmbedding - Node2vec 图文详解
一.引言
前面介绍了如何生成带权的图: GraphEmbedding - networkx获取图结构
从带权的图随机游走生成序列: GraphEmbedding - DeepWalk 随机游走
embedding 向量的评估与可视化: GraphEmbedding - embedding 向量的降维与可视化
以及复杂度O(1)的采样算法 Alias: GraphEmbedding - Alias 采样图文详解
还有二叉树搜索的 DFS 与 BFS: 二叉树的遍历 DFS 与 BFS
结合上面5个知识点，今天引出 Node2vec 算法，Node2vec 结合了上面几篇文章的内容，同时也引进了自己的创新，比 DeepWalk 更常见也更有效。
二.Node2vec 算法
1.Node2vec 简介
说起 Node2vec 还是要提一下 DeepWalk，DeepWalk 基于图随机游走，默认各个边的权重为1，其更偏向于 DFS 即深度优先搜索，DFS 的好处是搜索的全局性好，但是对于较远的邻居的 embedding 表征作用不大，这时还有 BFS 广度优先搜索，其对周围邻居的覆盖程度较高，但是搜索偏局部，无法感知稍远的邻居节点，Node2vec 的出现就是结合 DFS 与 BFS 的优点，从而对局部和全局进行了折中，得到了质量更高的采样序列。
2.Node2vec 理论
A.基于 Edge 的转移概率
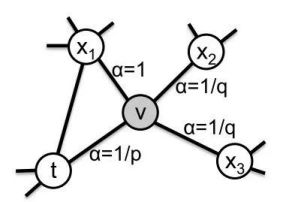
上面提到了DFS 和 BFS，在 Node2vec 中，通过 p,q 参数控制游走更偏向于全局搜索 DFS 还是局部搜索 BFS，假设当前节点从 t 走到 v 点，从 v 选择下一个邻居节点时，不再是等概率随机选择，而是对原始权重进行 P,Q修正，最终归一化得到选择不同节点的概率。
代表v的邻居与上一个起始点t的关系
=0 代表v又重新返回起始点t，其边权重的修正参数为 α=1/p
=1 代表从新起点v出发到达的下一个邻居和上一个起始点t也存在边的关系，此时距离为1,α=1
=2 代表从新起点v出发到达的下一个邻居与上一个起始点t不存在关系，所以距离为2, α=1/q
基于调节参数 和边的原始权重 
可以得到上一条路径为 t -> v，v向其邻居 
的整体转移概率，我们称之为基于edge的转移概率:
![[P(transform | (t,v)) = \alpha_{pq}(t,x) * w_{t,x} \ \ for \ x \ \in N(x)]](http://img.e-com-net.com/image/info8/2c00c0745069462ead2d2c32e0b9498a.gif){kind=small}
B.基于 Node 的转移概率
除了基于 edge 的转移概率，还有最基础的基于节点的转移概率，此时不考虑p,q参数，因为不涉及距离问题，从顶点 u 出发到任意u的邻居其距离均为1，所以 
均为1，此时 α=1，原始权重为 ，对于任意一点 v，v向其邻居 的整体转移概率，我们称之为基于 node 的转移概率:
![[P(transform | (t,v)) = w_{t,x} \ \ for \ x \ \in N(x)]](http://img.e-com-net.com/image/info8/2c1a7c423dc5495dbae18ab9ae85afba.gif){kind=small}
C.采样
基于图中所有 Node 的转移概率与 Edge 的转移概率，结合 Alias 生成 AliasTable，后续按概率 AliasSample 即可，通过调整 p,q 参数，调整游走序列在 DFS 和 BFS 的偏重：
P: 采样中 p 控制从 v 回到起始点 t 的概率，所以是回撤概率，p越大，回撤的概率越小
Q: 采样中 q 控制 t->v-> 新节点的概率，如果 q > 1 游走偏向于访问局部的节点(BFS)，因为此时 1>1/q ，如果 q < 1，游走偏向于访问全局的节点(DFS)，因为此时 1 < 1/q
3.Node2vec 伪代码
A.node2vecWalk
这部分负责随机游走生成关注关系序列，需要用到原始node u，游走长度 l，对当前节点进行 AliasSample 获取游走序列
B.LearnFeatures
除了初始化游走长度外，定义向量维度 d，回撤概率 p，转出概率 q，最后通过 stochastic gradient descent 随机梯度下降的学习器对 walk 得到的的多个序列 walks 训练，得到每个节点的 embedding，这里常用的是 Word2vec
三.Node2vec 实践
根据上面的 node2vevWalk 与 leranFeatures 我们大致理一下需要哪些步骤:
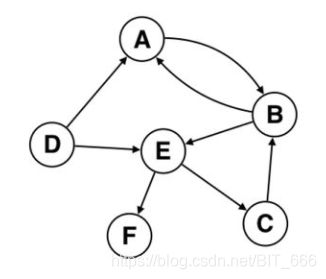
A.生成一个带权的关注关系图，并获取图中节点，边以及对应的权重
B.为每一个点，每一条边生成基于 Node 和基于 Edge 的转移概率并生成 Alias Table
C.根据epoch和walk length 以及 Alias Table 进行 Alias Sample 获取游走序列
D.通过 Word2vec 方法对数据训练并获得向量 Embedding
跟随上面的思路操作一下
1.生成带权图
1-1 构造图通过 Random 随机模拟关注关系图的原始节点与权重，node_num 控制节点数，sample_num 控制该关系图的边的大致数量
1-2 获取带权图，通过 networkx 读取 1.1 生成的图并加载权重 weight
1-3 通过 .nodes() 和 .edges() 方法获取模拟图的节点与边
# 1-1 构造图
edge_file = "./data/test_edges.txt"
node_num = 100
sample_num = 1000
def createGraph():
f = open(edge_file, "w")
for i in range(sample_num):
from = random.randint(0, node_num)
to = random.randint(0, node_num)
weight = random.random()
if from != to:
f.write("%s %s %s\n" % (from, to, weight))
f.close()
createGraph()
# 1-2 获取带权图
def loadGraph(fileName):
G = nx.read_edgelist(fileName, create_using=nx.DiGraph(), nodetype=None, data=[('weight', float)])
return G
G = loadGraph(edge_file)
# 1-3 获取图的节点与边
nodes = G.nodes()
edges = G.edges()
nodes_list = list(nodes)2.生成Alias Table
2.1 create_alias_table 方法通过将转移概率归一化并生成对应的 Alias Table，建表复杂度 O(n)，这里再重复一下之前的需求，Node2vec 在概率游走前需要进行初始化，获取 Node 的转移概率表 alias_nodes 和 Edge 的转移概率表 alias_edge，前者决定当前顶点需要访问的下一个节点的 Alias Table，后者则决定条件概率下 (t,v) 边访问到 v 点时，v 的下一个节点的 Alias Table
import numpy as np
def create_alias_table(transform_prob):
print("归一化前:", transform_prob)
# 当前node的邻居的nbr的转移概率之和
norm_const = sum(transform_prob)
# 当前node的邻居的nbr的归一化转移概率
normalized_prob = [float(u_prob) / norm_const for u_prob in transform_prob]
print("归一化后:", normalized_prob)
length = len(transform_prob)
# 建表复杂度o(N)
accept, alias = [0] * length, [0] * length
# small,big 存放比1小和比1大的索引
small, big = [], []
# 归一化转移概率 * 转移概率数
transform_N = np.array(normalized_prob) * length
print("归一化 * N 后:", transform_N)
# 根据概率放入small large
for i, prob in enumerate(transform_N):
if prob < 1.0:
small.append(i)
else:
big.append(i)
while small and big:
small_idx, large_idx = small.pop(), big.pop()
accept[small_idx] = transform_N[small_idx]
alias[small_idx] = large_idx
transform_N[large_idx] = transform_N[large_idx] - (1 - transform_N[small_idx])
if np.float32(transform_N[large_idx]) < 1.:
small.append(large_idx)
else:
big.append(large_idx)
while big:
large_idx = big.pop()
accept[large_idx] = 1
while small:
small_idx = small.pop()
accept[small_idx] = 1
return accept, alias2.2 计算 Edge 的条件转移概率
这里 p，q 即为回撤概率和深度搜索概率，可以进行调节，内部 for 循环就是根据上图和 
的距离进行节点间的权重生成
def get_alias_edge(G, t, v, p=1.0, q=1.0):
G = G
p = p
q = q
unnormalized_probs = []
# T -> V 对于V的邻居 nbr=T dtx=0 | 1步到位 dtx=1 | T -> V -> V-nbr dtx=2
for x in G.neighbors(v):
weight = G[v][x].get('weight', 1.0) # w_vx
if x == t: # d_tx == 0
unnormalized_probs.append(weight / p)
elif G.has_edge(x, t): # d_tx == 1
unnormalized_probs.append(weight)
else: # d_tx = 2
unnormalized_probs.append(weight / q)
norm_const = sum(unnormalized_probs)
normalized_probs = [float(u_prob) / norm_const for u_prob in unnormalized_probs]
return create_alias_table(normalized_probs)2.3 统一生成 Node Alias Table 和 Edge Alias Table
这里通过传入的参数 Graph 获取图的节点与边，节点直接调用 create_alias_table 制表，边则通过 get_alias_edge 加工制表
def preprocess_transition_probs(G):
alias_nodes = {}
for node in G.nodes():
# 当前node的邻居nbr的转移概率
unnormalized_probs = [G[node][nbr].get('weight', 1.0)
for nbr in G.neighbors(node)]
# 当前node的邻居的nbr的转移概率之和
norm_const = sum(unnormalized_probs)
# 当前node的邻居的nbr的归一化转移概率
normalized_probs = [
float(u_prob) / norm_const for u_prob in unnormalized_probs]
# 获取 Accept Alias: 前者为当前方式事件I的概率 后者为另一个事件的编号
alias_nodes[node] = create_alias_table(normalized_probs)
alias_edges = {}
for edge in G.edges():
alias_edges[edge] = get_alias_edge(G, edge[0], edge[1], p=0.25, q=4)
return alias_nodes, alias_edges
(alias_nodes, alias_edges) = preprocess_transition_probs(G)
3.概率游走获取序列
通过前面的准备工作已经获得了点与边的转移概率，下面开始概率游走:
3-1 alias_sample 负责从 alias_table 中 O(1) 的采样
def alias_sample(accept, alias):
N = len(accept)
i = int(np.random.random() * N)
r = np.random.random()
if r < accept[i]:
return i
else:
return alias[i]3-2 node2vec，铺垫了这么多，Node2walk 主要步骤都在这里，这里需要通过 walk 的长度判断是起始点还是中间点，起始点使用 alias_nodes，中间点使用 alias_edges
def node2vec_walk(G, _alias_nodes, _alias_edges, walk_length, start_node):
G = G
# 起始点
walk = [start_node]
while len(walk) < walk_length:
# 获取当前node
cur = walk[-1]
# 获取当前node的邻居
cur_nbrs = list(G.neighbors(cur))
# 如果有邻居
if len(cur_nbrs) > 0:
# 有邻居且当前为初始点 无顶点情况 使用alias_nodes
if len(walk) == 1:
walk.append(
cur_nbrs[alias_sample(_alias_nodes[cur][0], _alias_nodes[cur][1])])
# 有邻居且不是初始点 有顶点情况 使用alias_edges
else:
prev = walk[-2]
edge = (prev, cur)
next_node = cur_nbrs[alias_sample(_alias_edges[edge][0],
_alias_edges[edge][1])]
walk.append(next_node)
else:
break
return walk3-3 将上述两者结合，定义 walk_length 和 迭代次数进行概率游走采样。这里定义了迭代次数 num_walks = 10，walk_length = 30，具体数值可根据实际场景调整
# 获取游走序列 Node2vec
num_walks = 10
walks = []
for _ in range(num_walks):
random.shuffle(nodes_list)
for node in nodes_list:
walk = node2vec_walk(G, alias_nodes, alias_edges, 30, node)
walks.append(walk)
print("Node2vec Walk数目:", len(walks))
# 统计游走序列去重词个数
word_set = set()
for walk in walks:
for word in walk:
word_set.add(word)
print("去重大小:", len(word_set))经过上面一系列操作，终于获取了游走序列:
4.Word2vec 训练获取向量
4-1 word2vec 训练
前面提到了使用现有库 from gensim.models import Word2Vec 直接训练，相关参数之前有过介绍，注意 gensim 版本不同 Word2vec 的参数可能有出入
# sentences: 训练语料
# min_count: 最低词频
# vector_size: 词嵌入维度,老版本为 size
# sg: 算法选择 0-CBOW 1-skip-gram
# hs: 是否使用层次softmax
# workers: 训练的并行度
# window: 窗口大小
# epochs: 训练轮次，老版本也用为 iter，报错的话可以换一下
# alpha: 学习率
# sample: 采样阈值，出现次数过多的词会被采样，可以参考 softmax 采样优化的方法
# cbow_mean: 0-sum 1-mean 用于 CBOW 时对上下文词向量的处理
kwargs = {"sentences": walks, "min_count": 0, "vector_size": 64, "sg": 1, "hs": 0, "workers": 3, "window": 5,
"epochs": 3}
model = Word2Vec(**kwargs)4-2 获取训练向量
通过模型获取向量，由于模型参数设置 min_count ，所以所有 node 都可以获取向量，实际场景中，词频较小的词可能不会获得向量表征
def get_embeddings(w2v_model, graph):
count = 0
invalid_word = []
_embeddings = {}
for word in graph.nodes():
if word in w2v_model.wv:
_embeddings[word] = w2v_model.wv[word]
else:
invalid_word.append(word)
count += 1
print("无效word", len(invalid_word))
print("有效embedding", len(_embeddings))
return _embeddings
embeddings = get_embeddings(model, G)
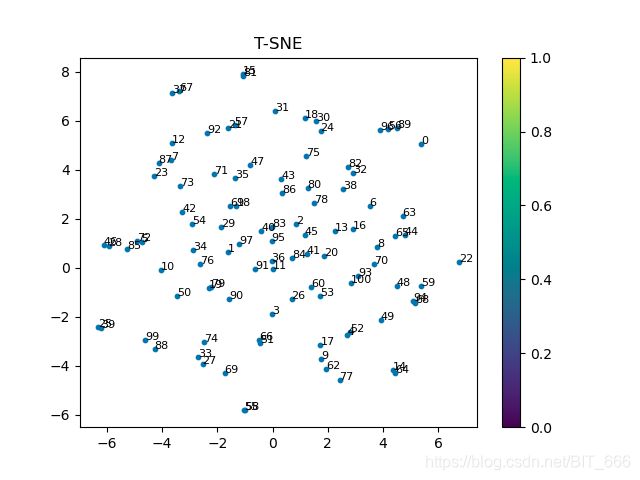
有兴趣也可以通过降维的方法对原始向量进行二维展示:
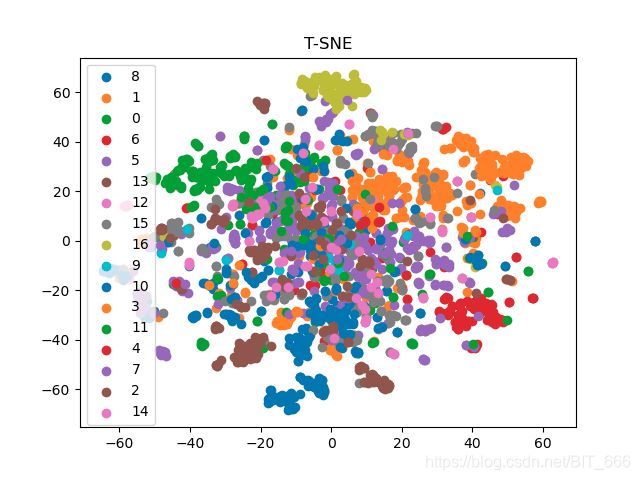
如果有原始数据的真实类别，可视化效果更好:
四.总结
Node2vec 相比 DeepWalk 优化了采样方式与序列生成方式，提高效率的情况下也提升了效果，这里简单介绍了使用的方法和过程，后续有时间继续盘一下 Line，SDNE，Struc2vec，EGES 等 GraphEmbedding 算法。