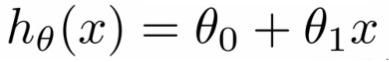Python实战：使用线性回归预测房价

房价大概是我们中国每一个普通老百姓比较关心的问题，我们想预测特定房子的价值，预测依据是房屋面积。

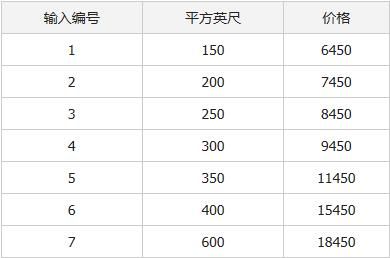
我们有下面的数据集：

在线性回归中，我们都知道必须在数据中找出一种线性关系，以使我们可以得到θ0和θ1。 我们的假设方程式如下所示：

其中： hθ(x)是关于特定平方英尺的价格值（我们要预测的值），（意思是价格是平方英尺的线性函数）； θ0是一个常数； θ1是回归系数。

那么现在开始编程：

步骤1

打开文本编辑器，并命名为predict_house_price.py。 我们在我们的程序中要用到下面的包，所以把下面代码复制到predict_house_price.py文件中去。

1 # Required Packages
2 import matplotlib.pyplot as plt
3 import numpy as np
4 import pandas as pd
5 from sklearn import datasets, linear_model

运行一下你的代码。如果程序没错，那步骤1基本做完了。如果你遇到了某些错误，这意味着你丢失了一些包，所以回头去看看包的页面。 安装博客文章中所有的包，再次运行你的代码。这次希望你不会遇到任何问题。

步骤2

把数据存储成一个.csv文件，名字为input_data.csv 所以让我们写一个函数把数据转换为X值（平方英尺）、Y值（价格）

1 # Function to get data
2 def get_data(file_name):
3 data = pd.read_csv(file_name)
4 X_parameter = []
5 Y_parameter = []
6 for single_square_feet ,single_price_value in zip(data['square_feet'],data['price']):
7 X_parameter.append([float(single_square_feet)])
8 Y_parameter.append(float(single_price_value))
9 return X_parameter,Y_parameter

第3行：将.csv数据读入Pandas数据帧。

第6-9行：把Pandas数据帧转换为X_parameter和Y_parameter数据，并返回他们。

所以，让我们把X_parameter和Y_parameter打印出来：

[[150.0], [200.0], [250.0], [300.0], [350.0], [400.0], [600.0]]
[6450.0, 7450.0, 8450.0, 9450.0, 11450.0, 15450.0, 18450.0]
[Finished in 0.7s]

脚本输出： [[150.0], [200.0], [250.0], [300.0], [350.0], [400.0], [600.0]] [6450.0, 7450.0, 8450.0, 9450.0, 11450.0, 15450.0, 18450.0] [Finished in 0.7s]

步骤3

现在让我们把X_parameter和Y_parameter拟合为线性回归模型。我们要写一个函数，输入为X_parameters、Y_parameter和你要预测的平方英尺值，返回θ0、θ1和预测出的价格值。

在学习过程中有什么不懂得可以加我的
python学习交流扣扣qun，784758214
群里有不错的学习视频教程、开发工具与电子书籍。
与你分享python企业当下人才需求及怎么从零基础学习好python，和学习什么内容
1 # Function for Fitting our data to Linear model
2 def linear_model_main(X_parameters,Y_parameters,predict_value):
3 
4 # Create linear regression object
5 regr = linear_model.LinearRegression()
6 regr.fit(X_parameters, Y_parameters)
7 predict_outcome = regr.predict(predict_value)
8 predictions = {}
9 predictions['intercept'] = regr.intercept_
10 predictions['coefficient'] = regr.coef_
11 predictions['predicted_value'] = predict_outcome
12 return predictions

第5-6行：首先，创建一个线性模型，用我们的X_parameters和Y_parameter训练它。

第8-12行：我们创建一个名称为predictions的字典，存着θ0、θ1和预测值，并返回predictions字典为输出。

所以让我们调用一下我们的函数，要预测的平方英尺值为700。

​

1 X,Y = get_data('input_data.csv')
2 predictvalue = 700
3 result = linear_model_main(X,Y,predictvalue)
4 print "Intercept value " , result['intercept']
5 print "coefficient" , result['coefficient']
6 print "Predicted value: ",result['predicted_value']

脚本输出：Intercept value 1771.80851064 coefficient [ 28.77659574] Predicted value: [ 21915.42553191] [Finished in 0.7s]

这里，Intercept value（截距值）就是θ0的值，coefficient value（系数）就是θ1的值。 我们得到预测的价格值为21915.4255——意味着我们已经把预测房子价格的工作做完了！

为了验证，我们需要看看我们的数据怎么拟合线性回归。所以我们需要写一个函数，输入为X_parameters和Y_parameters，显示出数据拟合的直线。

1 # Function to show the resutls of linear fit model
2 def show_linear_line(X_parameters,Y_parameters):
3 # Create linear regression object
4 regr = linear_model.LinearRegression()
5 regr.fit(X_parameters, Y_parameters)
6 plt.scatter(X_parameters,Y_parameters,color='blue')
7 plt.plot(X_parameters,regr.predict(X_parameters),color='red',linewidth=4)
8 plt.xticks(())
9 plt.yticks(())
10 plt.show()

那么调用一下show_linear_line函数吧：

1 show_linear_line(X,Y)

脚本输出：

对Python感兴趣或者是正在学习的小伙伴，可以加入我们的Python学习扣qun：784758214，看看前辈们是如何学习的！从基础的python脚本到web开发、爬虫、django、数据挖掘等，零基础到项目实战的资料都有整理。送给每一位python的小伙伴！每天都有大牛定时讲解Python技术，分享一些学习的方法和需要注意的小细节，点击加入我们的 python学习者聚集地

以上就是本文关于Python编程实现使用线性回归预测数据的全部内容，觉得文章还可以的话不妨收藏起来慢慢看，有任何意见或者看法欢迎大家评论！