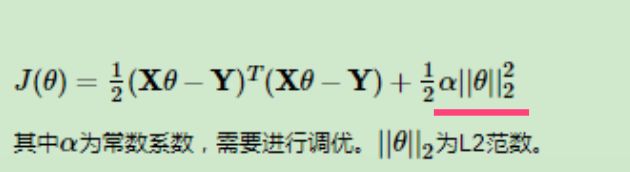线性回归-预测房价（机器学习）
机器学习-线性回归-预测房价
导入我们需要的模块包
import pandas as pd
import numpy as np
import matplotlib as plt
import seaborn
读取数据，查看数据
header = None表示不设置，表格的首字段。
# 读取训练集
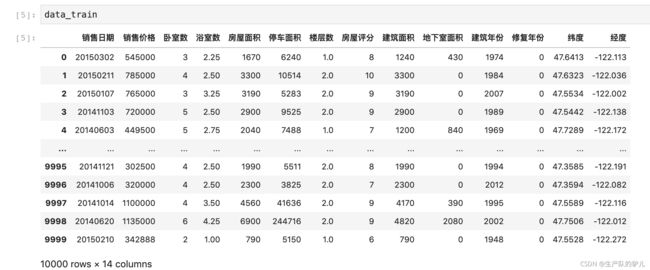
data_train = pd.read_csv('kc_train.csv',header = None)
#给数据标列名
data_train.columns =["销售日期","销售价格","卧室数","浴室数","房屋面积","停车面积","楼层数","房屋评分",
"建筑面积","地下室面积","建筑年份","修复年份","纬度","经度"]
# 读取测试集
t = pd.read_csv('kc_test.csv')
训练集
测试集
关于数据的介绍
数据分为两个csv文件，一个是用来训练的数据集。
另一个是用来检测数据，是通过 训练出来的数据集 进行 房价的预测，对比真实的结果。
将我们需要的目标值，进行提取
target=data_train['销售价格'] # 提取出目标值
将我们需要的特征值，进行提取
housing = data_train.drop(columns = ['销售价格'])
检查特指值的数据是否缺失
housing.info() # 查看数据是否有缺失值
对特征值的数据进行标准化
# 特征缩放数据
from sklearn.preprocessing import MinMaxScaler
minmax_scaler=MinMaxScaler()
minmax_scaler.fit(housing) #计算四个值：均值，方差，最大值，最小值
scaler_housing=minmax_scaler.transform(housing) # 标准化 处理特征值（根据上面计算出来的四个值）
scaler_housing=pd.DataFrame(scaler_housing,columns=housing.columns) #将处理后特征值转为dataframe处理
选择模型进行训练
这里选择的是 多元线性回归模型，也可以考虑替换成其他模型进行数据的训练
# 选择线性回归模型（正规方程）
from sklearn.linear_model import LinearRegression
LR_reg = LinearRegression()
# 进行拟合
LR_reg.fit(scaler_housing,target)
正规方程 sklearn.linear_model.LinearRegression
梯度下降 sklearn.linear_model.SGDRegressor
from sklearn.linear_model import SGDRegressor
# 选择线性回归模型（梯度下降）
LR_reg = LinearRegression()
# 进行拟合
LR_reg.fit(scaler_housing,target)
正规方程和梯度下降的不同点
线性回归模型，如果特征值过多，会可能存在过拟合的现象。
小tips:
科普过拟合和欠拟合
欠拟合： 数据的特征值过少，不能很好的拟合。
过拟合：数据的特征值过多， 存在嘈杂特征，模型过于复杂导致模型的泛化性不够。
如何解决过拟合：
假设我们通过线性回归生成的数据模型如下：
关于线性回归的模型
进行模型好坏的评估
这里使用的均方进行模型的评估，当然也可以考虑替换成其他模型进行模型好坏的评估
# 使用均方误差评估模型的好坏
from sklearn.metrics import mean_squared_error
preds = LR_reg.predict(scaler_housing) #输入数据预测得到结果
mse = mean_squared_error(preds,target) #使用均方误差来评价模型好坏，可以输出mse进行查看评价值
绘制出预测值和真实值的线进行对比
import matplotlib.pyplot as plt
# 绘图进行比较
plt.figure(figsize = (10,7))
num = 100
x = np.arange(1,num+1) # 取100个点进行比较
plt.plot(x,target[:num],label='target') # 目标值
plt.plot(x,preds[:num],label='preds') # 预测值
plt.legend(loc='upper right') # 把标放在右上角
plt.show()
将预测出来的结果导出
# 输出测试数据
result = LR_reg.predict(scaler_housing)
df_result = pd.DataFrame(result)
df_result.to_csv('result.csv')
这里写一下自己做到这里错误点。。。。
这里绘制出来的图像，分别是用的训练集的数据，进行导出来的 预测结果， 和 训练集的真实结果进行对比所绘制出来的图像。
建议采用 测试集的数据 使用训练出来的模型， 对比其的预测结果 和 真实值的对比图像。
当我发现，测试集的数据，并没有给销售价格的那一列，所以，应该是当模型循环完毕后，
测试集的数据是用来，预测去房价的。并不能用来对比。
后面尝试对模型的其他方面修改微调的其它方面
主要是红色部分的调整
模型评价是根据 训练模型的不同而不同
数据预处理部分
训练的模型
线性回归 Linear Regression
定义：
全部由 线性 变量 组成的回归模型
其中a为系数，x是变量，b为偏置。因为这个函数只有线性关系，所以只适用于建模线性可分数据。
特点：
1.建模速度快，数据量大的情况下依然可以。
2. 可以根据系数给出每个变量的理解和解释
3. 对异常值很敏感
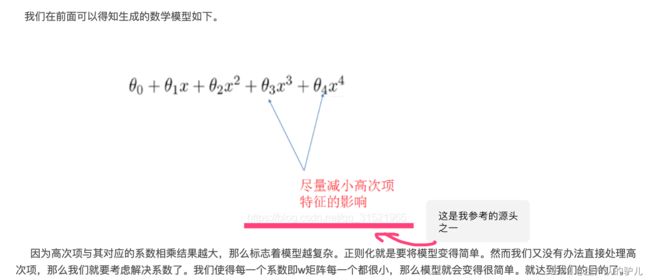
多项式回归 Polynomial Regression
定义：
用于 非线性 可分的数据 时可以使用多项式回归
曲线来拟合数据点
特点：
- 拟合非线性可分的数据
- 设置变量的指数，所以它是完全控制要素变量的建模
- 需要对数据进行了解 的 先验知识，不然容易出现过拟合现象
岭回归 Ridge Regression
自变量 之间的 会存在相似性，从而影响模型的构建。
回归分析需要我们了解每个变量与输出之间的关系，
高共线性就是说自变量间存在某种函数关系，
如果两个自变量（X1和X2）之间存在函数关系，那么当X1改变一个单位时，X2也会相应的改变，这样就没办法固定其他条件来对单个变量对输出的影响进行分析了。
因为分析的X1总是混杂了X2的作用，这样就造成了分析误差，回归分析时需要排除高共线性的影响。
如何确定哪些特征值/自变量之间存在高共线性：
- 尽管从理论上讲，该变量与Y高度相关，但是回归系数却不明显
- 添加或删除X特征变量时，回归系数会发生明显变化
- X特征变量具有较高的成对相关性（pairwise correlations）(检查相关矩阵)
岭回归是针对模型中存在的共线性关系的为变量增加一个小的平方偏差因子(也就是正则项)，
可以表示成下面的式子：
平方偏差因子向模型中引入了少量偏差，但大大减少了方差。
岭回归特点：
增加
将 选择模型进行训练部分 修改为 选择 岭回归模型 进行数据的训练
# 选择岭回归模型（基于梯度下降）
from sklearn.linear_model import Ridge
RR_reg = Ridge(alpha = 0.5)
# # 进行拟合
RR_reg.fit(scaler_housing,target)
超参数alpha：正则化的力度，取值范围0~1
正则化力度越大，那么权重系数会越小。而正则化力度越小，权重系数会越大。
对比 线性回归的 mse 最小均方误差
线性回归
岭回归
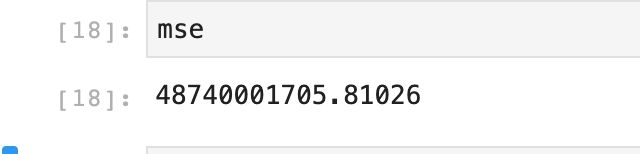
岭回归通过对系数的大小施加惩罚来解决 普通最小二乘的一些问题
拓展岭回归实现交叉验证
Lasso回归
又称为L1正则化。
正则化 分为两种 L1正则化 和 L2正则化。
主要是为了防止模型的过拟合，才采用的。
公式如下：
用于对比，岭回归的L2正则化公式如下：
弹性网络回归(ElasticNet Regression)
模型好坏的评估（根据选择训练的模型的不同而改变）
暂时先写这里，我得去研究一下RNN时间序列，不过定一个小目标，下个礼拜周末结束前，将这个内容整理完毕。
日期在11月1日前完成。