Leetcode 第56场双周赛 / 第249场周赛 / 1411. 给 N x 3 网格图涂色的方案数(这次主要还是学动规思想和迪杰斯克拉)
第56场双周赛
这次第一次进前五百,有点开心
5792. 统计平方和三元组的数目
题目描述
一个 平方和三元组 (a,b,c) 指的是满足 a2 + b2 = c2 的 整数 三元组 a,b 和 c 。
给你一个整数 n ,请你返回满足 1 <= a, b, c <= n 的 平方和三元组 的数目。
示例 1:
输入:n = 5
输出:2
解释:平方和三元组为 (3,4,5) 和 (4,3,5) 。
示例 2:
输入:n = 10
输出:4
解释:平方和三元组为 (3,4,5),(4,3,5),(6,8,10) 和 (8,6,10) 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-square-sum-triples
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
计算两数平方之和的平方根,然后判断平方根的平方是否等于两数平方之和
class Solution {
public int countTriples(int n) {
int res = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
int c = i * i + j * j;
int t = (int)Math.sqrt(c);
if(t <= n && t * t == c)
res++;
}
}
return res;
}
}
5793. 迷宫中离入口最近的出口
给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 ‘.’ 表示)和墙(用 ‘+’ 表示)。
同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。
你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。
输入:maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
输出:1
解释:总共有 3 个出口,分别位于 (1,0),(0,2) 和 (2,3) 。
一开始,你在入口格子 (1,2) 处。
输入:maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
输出:2
解释:迷宫中只有 1 个出口,在 (1,2) 处。
(1,0) 不算出口,因为它是入口格子。
初始时,你在入口与格子 (1,0) 处。
- 你可以往右移动 2 步到达 (1,2) 处。
所以,最近的出口为 (1,2) ,距离为 2 步。
示例 3:
输入:maze = [[".","+"]], entrance = [0,0]
输出:-1
解释:这个迷宫中没有出口。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/nearest-exit-from-entrance-in-maze
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
典型迷宫计算最少步数的题,广度优先搜索,当时写的时候,明知应该用bfs,还是先写了个dfs结果提交超时了,又改了个bfs,作死。。
class Solution {
int[][] direction = {{1,0},{-1,0},{0,1},{0,-1}};
int m;
int n;
boolean[][] used;
public int nearestExit(char[][] maze, int[] entrance) {
m = maze.length;
n = maze[0].length;
used = new boolean[m][n];
int i = entrance[0];
int j = entrance[1];
used[i][j] = true;
int step = 0;
Queue<int[]> queue = new LinkedList<>();
queue.offer(entrance);
while(!queue.isEmpty()){
int size = queue.size();
step++;
while(size-- > 0){
int[] temp = queue.poll();
for(int k = 0; k < 4; k++){
int x = temp[0] + direction[k][0];
int y = temp[1] + direction[k][1];
if(!check(x, y)){
if(step != 1){
return step - 1;
}
continue;
}
if(maze[x][y] == '+' || used[x][y])
continue;
queue.add(new int[]{x, y});
used[x][y] = true;
}
}
}
return -1;
}
public boolean check(int x, int y){
return x >= 0 && x < m && y >= 0 && y < n;
}
}
5794. 求和游戏
题目描述
Alice 和 Bob 玩一个游戏,两人轮流行动,Alice 先手 。
给你一个 偶数长度 的字符串 num ,每一个字符为数字字符或者 ‘?’ 。每一次操作中,如果 num 中至少有一个 ‘?’ ,那么玩家可以执行以下操作:
选择一个下标 i 满足 num[i] == ‘?’ 。
将 num[i] 用 ‘0’ 到 ‘9’ 之间的一个数字字符替代。
当 num 中没有 ‘?’ 时,游戏结束。
Bob 获胜的条件是 num 中前一半数字的和 等于 后一半数字的和。Alice 获胜的条件是前一半的和与后一半的和 不相等 。
比方说,游戏结束时 num = “243801” ,那么 Bob 获胜,因为 2+4+3 = 8+0+1 。如果游戏结束时 num = “243803” ,那么 Alice 获胜,因为 2+4+3 != 8+0+3 。
在 Alice 和 Bob 都采取 最优 策略的前提下,如果 Alice 获胜,请返回 true ,如果 Bob 获胜,请返回 false 。
示例 1:
输入:num = “5023”
输出:false
解释:num 中没有 ‘?’ ,没法进行任何操作。
前一半的和等于后一半的和:5 + 0 = 2 + 3 。
示例 2:
输入:num = “25??”
输出:true
解释:Alice 可以将两个 ‘?’ 中的一个替换为 ‘9’ ,Bob 无论如何都无法使前一半的和等于后一半的和。
示例 3:
输入:num = “?3295???”
输出:false
解释:Bob 总是能赢。一种可能的结果是:
- Alice 将第一个 ‘?’ 用 ‘9’ 替换。num = “93295???” 。
- Bob 将后面一半中的一个 ‘?’ 替换为 ‘9’ 。num = “932959??” 。
- Alice 将后面一半中的一个 ‘?’ 替换为 ‘2’ 。num = “9329592?” 。
- Bob 将后面一半中最后一个 ‘?’ 替换为 ‘7’ 。num = “93295927” 。
Bob 获胜,因为 9 + 3 + 2 + 9 = 5 + 9 + 2 + 7 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/sum-game
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
第一眼看到是这种题感觉凉了,最后根据数据范围排除了复杂的方法有惊无险做出来了
我是这样想的,首先求出前后半段和,还有前后半段有几个问号
然后因为操作是交替进行的,所以两个人如果填在不同边(指前后不同),那么就可以填相同的数相互抵消。
而如果前面sum之和大于后面sum之和,而且前面的?也比后面的多,那么两边之和肯定不相同,肯定Alice胜利
同理,后面sum之和大于前面sum之和,后面?也比前面多,那么Alice胜利
如果前后和还有?都相同,那么Bob可以通过在不同段填和Alice一样的数 来保证胜利
剩下两种情况就是前面大于等于后面和,但是前面的?比后面的少,或者反过来,那么这种怎么想呢?
我想的是先前后抵消,然后此时需要在后面填 k 个空,使得和为 differ。
如果此时?为奇数个,那么不管Bob最后一次怎么填,Alice都可以使结果不相同,Alice必胜
如果为偶数个,那么Bob进行最后一次操作,就有可能扭转局面哈哈,什么情况下才能扭转呢。
两人一个填k个空,也就是一个人填count次,和要等于differ,而Alice是不想让Bob赢的,如果differ大于或者小于9*count,那么Alice可以只填0或者只填9来使和不可能等于differ,而只有等于9 *count的时候,Alice填了一个数x,那么Bob就填9-x来保证每一组数都是9,从而获得胜利
class Solution {
public boolean sumGame(String num) {
//Bob能获胜的话,是不管怎么添数,前后都相同
char[] ss = num.toCharArray();
int l = ss.length;
int presum = 0;
int postsum = 0;
int pre = 0;
int post = 0;
for(int i = 0; i < l / 2; i++){
if(ss[i] == '?')
pre++;
else
presum += ss[i] - '0';
}
for(int i = l / 2; i < l; i++){
if(ss[i] == '?')
post++;
else
postsum += ss[i] - '0';
}
System.out.println(pre);
System.out.println(post);
System.out.println(presum);
System.out.println(postsum);
if(presum > postsum && pre >= post)
return true;
if(presum < postsum && pre <= post)
return true;
if(presum == postsum && pre == post)
return false;
if(presum >= postsum && pre < post){
int sum = presum - postsum;
int kong = post - pre;
int count = kong / 2;
System.out.println(kong);
if(kong % 2 == 0 && count * 9 == sum)
return false;
}
if(presum <= postsum && pre > post){
int sum = postsum - presum;
int kong = pre - post;
int count = kong / 2;
if(kong % 2 == 0 && count * 9 == sum)
return false;
}
return true;
}
}
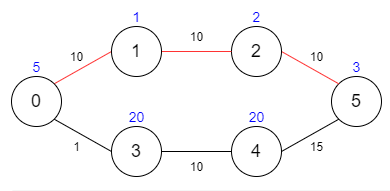
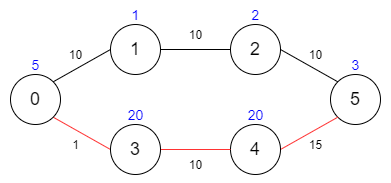
5795. 规定时间内到达终点的最小花费
题目描述
一个国家有 n 个城市,城市编号为 0 到 n - 1 ,题目保证 所有城市 都由双向道路 连接在一起 。
道路由二维整数数组 edges 表示,其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路,耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路,但是不会有道路两头连接着同一座城市。
每次经过一个城市时,你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示,其中 passingFees[j] 是你经过城市 j 需要支付的费用。
一开始,你在城市 0 ,你想要在 maxTime 分钟以内 (包含 maxTime 分钟)到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 (包括 起点和终点城市的通行费)。
给你 maxTime,edges 和 passingFees ,请你返回完成旅行的 最小费用 ,如果无法在 maxTime 分钟以内完成旅行,请你返回 -1 。
输入:maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:11
解释:最优路径为 0 -> 1 -> 2 -> 5 ,总共需要耗费 30 分钟,需要支付 11 的通行费。
示例 2:
输入:maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:48
解释:最优路径为 0 -> 3 -> 4 -> 5 ,总共需要耗费 26 分钟,需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ,因为这条路径耗费的时间太长。
示例 3:
输入:maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:-1
解释:无法在 25 分钟以内从城市 0 到达城市 5 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-cost-to-reach-destination-in-time
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
做完第三道还有三分钟,这道题都没来的及看…
按照大佬的思路写了个动态规划,但是超时了,不知道为什么,感觉一样的啊,C++能过,java过不了
动态规划的思路是这样,先预处理邻接矩阵
然后dp[t][i]定义为t时间内能到达位置i 的最少花费
初始化很重要,因为任意时间,只要不走动,都在0位置,所以dp[t][0] = passingFees[0]
而转移的时候,也和一般转移情况不同,而是对于当前时刻位置,找能转移的点转移。而不是和一般情况一样,在当前点找之前的点转移。因为要保证是从0位置开始往后走,所以这样进行转移
超时看了一下,应该是因为第三层循环,这里C++代码里面是这样写的
for (auto [v, w] : adj[i])
这样写取的也是从i开始可以到达的点,为啥这里不会超时。而且给出的时间复杂度也没有计算这层循环,看了一下这种写法用java能过的,是把i到达的点用哈希表存储起来了。。实际上感觉还是遍历,只不过遍历的范围少了一点,这里就不改了,懂这个意思就行了
class Solution {
public int minCost(int maxTime, int[][] edges, int[] passingFees) {
//这道题咋说呢,感觉应该能写出来,毕竟思路很明确
//dp[i][j]为在i时刻前到达j城市的最小花费
//那么转移方程就应该是所有能到达j的城市x花费的最小值,dp[i][j] = min(dp[i - t][x] + cost)
int n = passingFees.length;
//邻接矩阵
int[][] adj = new int[n][n];
//赋初值,不可达
for(int i = 0; i < n; i++){
Arrays.fill(adj[i], Integer.MAX_VALUE);
}
for(int[] edge : edges){
int pos1 = edge[0];
int pos2 = edge[1];
int time = edge[2];
if(time > maxTime)
continue;
if(adj[pos1][pos2] == Integer.MAX_VALUE || adj[pos1][pos2] > time){
adj[pos1][pos2] = time;
adj[pos2][pos1] = time;
}
}
//动态规划
int[][] dp = new int[maxTime + 1][n];
for(int i = 0; i <= maxTime; i++){
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
//初始化,任意时刻在0位置,有花费passingFees[0]
for(int i = 0; i <= maxTime; i++){
dp[i][0] = passingFees[0];
}
//dp[0][0] = passingFees[0];
for(int t = 0; t < maxTime; t++){
for(int i = 0; i < n; i++){
//如果在t时刻无法到达 i 位置,那么跳过
if(dp[t][i] == Integer.MAX_VALUE)
continue;
//然后遍历当前位置所有能到达的点
for(int pos = 0; pos < n; pos++){
//如果两个点不可达
if(adj[i][pos] == Integer.MAX_VALUE)
continue;
//如果可达
int time = adj[i][pos];
//超时了
if(t + time > maxTime)
continue;
//在规定时间内能到达的点,花的费用就是达到该点要的费用
dp[t + time][pos] = Math.min(dp[t + time][pos], dp[t][i] + passingFees[pos]);
}
}
}
//处理完后,输出
return dp[maxTime][n - 1] == Integer.MAX_VALUE ? -1 : dp[maxTime][n - 1];
}
}
写一下官解给的动规看行不行
这个思路减少了邻接矩阵的创建,另外转移方程就和常规转移思路一样
这里比较难理解的点是,为什么每次只遍历edges矩阵就可以保证输出是合理的。
因为这里如果不是从0位置开始走的话,dp[t][i]的值是很大的,这样就保证了结果是从0出发的
class Solution {
public int minCost(int maxTime, int[][] edges, int[] passingFees) {
//这道题咋说呢,感觉应该能写出来,毕竟思路很明确
//dp[i][j]为在i时刻前到达j城市的最小花费
//那么转移方程就应该是所有能到达j的城市x花费的最小值,dp[i][j] = min(dp[i - t][x] + cost)
int n = passingFees.length;
//动态规划
int[][] dp = new int[maxTime + 1][n];
for(int i = 0; i <= maxTime; i++){
Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
}
//初始化,任意时刻在0位置,有花费passingFees[0]
for(int i = 0; i <= maxTime; i++){
dp[i][0] = passingFees[0];
}
//dp[0][0] = passingFees[0];
for(int t = 1; t <= maxTime; t++){
//遍历所有的边
for(int[] edge : edges){
int pos1 = edge[0];
int pos2 = edge[1];
int time = edge[2];
//时间不够跳过
if(t < time)
continue;
//从pos2到达pos1
dp[t][pos1] = Math.min(dp[t][pos1], dp[t - time][pos2] + passingFees[pos1]);
//从pos1到达pos2
dp[t][pos2] = Math.min(dp[t][pos2], dp[t - time][pos1] + passingFees[pos2]);
}
}
//处理完后,输出
return dp[maxTime][n - 1] == Integer.MAX_VALUE / 2 ? -1 : dp[maxTime][n - 1];
}
}
再来写迪杰斯特拉算法
迪杰斯特拉算法是基于贪心策略的,就是从原点开始扩展,找到距离原点最短距离的点,然后将这个点标记为true,意思是找到了到达这个点的最短路径,并且根据当前这个点更新邻接矩阵。下次找,还是找距离原点最近的点,重复上述步骤,直到扩展完所有点
本题就是加了一个时间,但是时间并不影响什么,只是将时间大于maxtime的话,就把这个路径舍弃。思路就是按最小的花费扩展,这里邻接矩阵必须写成哈希表的形式,写成数组还是会超时
class Solution {
public int minCost(int maxTime, int[][] edges, int[] passingFees) {
//自己写一下迪杰斯特拉算法
int n = passingFees.length;
//首先建立邻接矩阵
//pos1, pos2, time
HashMap<Integer, Map<Integer, Integer>> map = new HashMap<>();
for(int[] edge : edges){
int pos1 = edge[0];
int pos2 = edge[1];
int time = edge[2];
if(time > maxTime)
continue;
Map<Integer, Integer> temp = map.getOrDefault(pos1, new HashMap<>());
int time2 = temp.getOrDefault(pos2, Integer.MAX_VALUE);
temp.put(pos2, Math.min(time, time2));
map.put(pos1, temp);
temp = map.getOrDefault(pos2, new HashMap<>());
time2 = temp.getOrDefault(pos1, Integer.MAX_VALUE);
temp.put(pos1, Math.min(time, time2));
map.put(pos2, temp);
}
//根据迪杰斯特拉算法的思想,创建一个优先队列,存储的是各个点的花费情况
//花费最小的放在头部,方便下一次进行扩展
PriorityQueue<int[]> pq = new PriorityQueue<>((int[] a, int[] b) -> (a[1] - b[1]));
//t时刻在i位置的花费
int[][] dis = new int[n][maxTime + 1];
boolean[][] vis = new boolean[n][maxTime + 1];
dis[0][0] = passingFees[0];
for (int i = 0; i < n; i++){
Arrays.fill(dis[i], Integer.MAX_VALUE);
}
//到达节点0,通行费为passingFees[0],时间为0
pq.offer(new int[]{0, passingFees[0], 0});
while(!pq.isEmpty()){
int[] temp = pq.poll();
//如果到末端了,就返回
if(temp[0] == n - 1)
return temp[1];
//如果当前已有的花费比这个花费少,不需要更新
if (dis[temp[0]][temp[2]] < temp[1]) continue;
if (vis[temp[0]][temp[2]]) continue;
vis[temp[0]][temp[2]] = true;
//找到当前点能到达的所有点
Map<Integer, Integer> mm = map.getOrDefault(temp[0], new HashMap<>());
if(mm.size() == 0)
continue;
for(int key : mm.keySet()){
//然后把这个点放入优先队列中
//计算时间
int time = mm.get(key) + temp[2];
if(time > maxTime)
continue;
//如果花费大于已有花费
if(temp[1] + passingFees[key] >= dis[key][time])
continue;
pq.offer(new int[]{key, temp[1] + passingFees[key], time});
//更新到达该点的花费
dis[key][time] = temp[1] + passingFees[key];
}
}
return -1;
}
}
第249场周赛
两道十来分钟做出来,第三道硬推了一个多小时没整明白…800多快900名
5808. 数组串联
题目描述
给你一个长度为 n 的整数数组 nums 。请你构建一个长度为 2n 的答案数组 ans ,数组下标 从 0 开始计数 ,对于所有 0 <= i < n 的 i ,满足下述所有要求:
ans[i] == nums[i]
ans[i + n] == nums[i]
具体而言,ans 由两个 nums 数组 串联 形成。
返回数组 ans 。
示例 1:
输入:nums = [1,2,1]
输出:[1,2,1,1,2,1]
解释:数组 ans 按下述方式形成:
- ans = [nums[0],nums[1],nums[2],nums[0],nums[1],nums[2]]
- ans = [1,2,1,1,2,1]
示例 2:
输入:nums = [1,3,2,1]
输出:[1,3,2,1,1,3,2,1]
解释:数组 ans 按下述方式形成:
- ans = [nums[0],nums[1],nums[2],nums[3],nums[0],nums[1],nums[2],nums[3]]
- ans = [1,3,2,1,1,3,2,1]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/concatenation-of-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
没啥说的
class Solution {
public int[] getConcatenation(int[] nums) {
int l = nums.length;
int[] res = new int[2 * l];
for(int i = 0; i < l; i++){
res[i] = nums[i];
}
for(int i = l; i < 2 * l; i++){
res[i] = nums[i - l];
}
return res;
}
}
5809. 长度为 3 的不同回文子序列
题目描述
给你一个字符串 s ,返回 s 中 长度为 3 的不同回文子序列 的个数。
即便存在多种方法来构建相同的子序列,但相同的子序列只计数一次。
回文 是正着读和反着读一样的字符串。
子序列 是由原字符串删除其中部分字符(也可以不删除)且不改变剩余字符之间相对顺序形成的一个新字符串。
例如,“ace” 是 “abcde” 的一个子序列。
示例 1:
输入:s = “aabca”
输出:3
解释:长度为 3 的 3 个回文子序列分别是:
- “aba” (“aabca” 的子序列)
- “aaa” (“aabca” 的子序列)
- “aca” (“aabca” 的子序列)
示例 2:
输入:s = “adc”
输出:0
解释:“adc” 不存在长度为 3 的回文子序列。
示例 3:
输入:s = “bbcbaba”
输出:4
解释:长度为 3 的 4 个回文子序列分别是:
- “bbb” (“bbcbaba” 的子序列)
- “bcb” (“bbcbaba” 的子序列)
- “bab” (“bbcbaba” 的子序列)
- “aba” (“bbcbaba” 的子序列)
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-length-3-palindromic-subsequences
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
想了一下动规,滑动窗口什么的,一维不知道咋做,就想别的了
总共26个字母,记录每个字母出现最前面和最后面的位置,然后统计中间的每个字母是否出现就行了
class Solution {
public int countPalindromicSubsequence(String s) {
int l = s.length();
char[] cc = s.toCharArray();
//滑动窗口吗
//先遍历一遍记录每个字母出现的最左最右位置
int[] left = new int[26];
Arrays.fill(left, -1);
int[] right = new int[26];
Arrays.fill(right, -1);
for(int i = 0; i < l; i++){
char c = cc[i];
if(left[c - 'a'] == -1){
left[c - 'a'] = i;
}
}
for(int i = l - 1; i >= 0; i--){
char c = cc[i];
if(right[c - 'a'] == -1){
right[c - 'a'] = i;
}
}
int res = 0;
for(int i = 0; i < 26; i++){
int le = left[i];
int r = right[i];
if(le == -1 || r == -1)
continue;
boolean[] used = new boolean[26];
for(int j = le + 1; j < r; j++){
char c = cc[j];
if(!used[c - 'a']){
used[c - 'a'] = true;
res++;
}
}
}
return res;
}
}
5811. 用三种不同颜色为网格涂色
题目描述
给你两个整数 m 和 n 。构造一个 m x n 的网格,其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足:不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大, 返回 对 109 + 7 取余 的结果。
示例 1:
输入:m = 1, n = 1
输出:3
解释:如上图所示,存在三种可能的涂色方案。
示例 2:
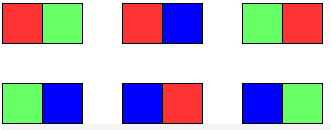
输入:m = 1, n = 2
输出:6
解释:如上图所示,存在六种可能的涂色方案。
示例 3:
输入:m = 5, n = 5
输出:580986
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/painting-a-grid-with-three-different-colors
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
现在才发现这个题是个困难,第三道就是困难。。难顶了。
刚开始就是按之前做过的一个房子涂三种颜色的想法做的,结果不对,发现变成二维的不知道咋转移了,然后就去找规律,结果也没找到,最后想着范围不大,直接爆搜吧,但是时间不够了。。
看了半天终于看懂了题解,感觉不是自己能做出来的范畴,想不到用这样一行一行转移的动态规划
首先,三种颜色对应0 1 2,因为所给的数据范围为m < = 5和n <= 1000,所以把m看成一行的长度,也就是列数
这样把每一行的涂色方案看成一个3进制数,所以这个3进制数的范围就是0到3的m次方
枚举这个范围内的所有数,也就是所有的涂色方案,判断相邻的位是否相同,来确定这一行的涂色方案
而计算下一行的涂色方案,也就是下一行的三进制数和当前行的三进制数,对应位数均不相同
定义dp[i][mask]就是在第i行涂色情况为mask的方案数
初始化,当i等于0时,需要单独处理
自己写一下:
class Solution {
public static final int MOD = (int)1.0e9 + 7;
//哈希表,键值是mask,
Map<Integer, int[]> map = new HashMap<>();
public int colorTheGrid(int m, int n) {
int mask = 0;
//先找第一行符合条件的mask
//最大,3的m次
int mask_end = (int)Math.pow(3, m);
while(mask < mask_end){
//存放当前颜色的数组
int[] temp = new int[m];
int index = 0;
int mask_tmep = mask;
for(int i = 0; i < m; i++){
int yushu = mask_tmep % 3;
temp[index++] = yushu;
mask_tmep = mask_tmep / 3;
}
//此时获得了当前颜色的数组temp
//判断相邻颜色是否相同
boolean flag = true;
for(int i = 1; i < m; i++){
//如果颜色相同,那么就不行,跳出
if(temp[i] == temp[i - 1]){
flag = false;
break;
}
}
//如果符合条件,那么加到哈希表中
if(flag){
map.put(mask, temp);
}
mask++;
}
//处理了第一行,处理相邻行的情况
//相邻行,与键值能相邻的值的情况
Map<Integer, Set<Integer>> adj = new HashMap<>();
for(Map.Entry<Integer, int[]> entry1 : map.entrySet()){
int key1 = entry1.getKey();
int[] value1 = entry1.getValue();
for(Map.Entry<Integer, int[]> entry2 : map.entrySet()){
int[] value2 = entry2.getValue();
boolean flag = true;
//判断上下是否相同
for(int i = 0; i < m; i++){
if(value1[i] == value2[i]){
flag = false;
break;
}
}
if(flag){
Set<Integer> set = adj.getOrDefault(key1, new HashSet<>());
set.add(entry2.getKey());
adj.put(key1, set);
}
}
}
//动态规划处理后面几行
int[][] dp = new int[n][mask_end];
//初始化
for(Map.Entry<Integer, int[]> entry : map.entrySet()){
int key1 = entry.getKey();
dp[0][key1] = 1;
}
for(int i = 1; i < n; i++){
//对于符合条件的涂色情况
for(Map.Entry<Integer, int[]> entry : map.entrySet()){
int key = entry.getKey();
//取到可以和key相邻的涂色情况
for(int t : adj.get(key)){
dp[i][key] = (dp[i][key] + dp[i - 1][t]) % MOD;
}
}
}
//最后结果就是最后一行的所有情况加起来
int res = 0;
for(int i = 0; i < mask_end; i++){
res = (res + dp[n - 1][i]) % MOD;
}
return res;
}
}
1411. 给 N x 3 网格图涂色的方案数
题目描述
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-ways-to-paint-n-3-grid
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
和上一道题一样,只不过这里规定了列数是3,还是一行一行递推,去看一下有没有什么别的方法学习一下
官解给了个递推优化的答案,就是说,一行三个格子的情况有12种:
010,012,020,021,101,102,120,121,201,202,210,212
这12种情况又可以分成两类,也就是ABA形的和ABC形式的,各6种
我们尝试找出这两类之间的递推关系
例如上一行是ABA类,下一行是ABA类,取一个例子,如上一行是010,那么下一行可以是101,121,202,三种
同理,上ABA,下ABC,取例子010,下就是102,201,两种
同理,上ABC,下ABA,两种;上ABC,下ABC两种
用两个变量表示上一行ABA、ABC两类的数量,然后根据这个关系递推n行,就能得到答案
这里写的时候要注意用long类型,否则在乘的时候需要对取余进行处理,比较麻烦
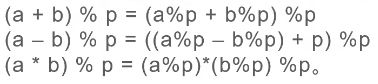
class Solution {
public static final int MOD = (int)1.0e9 + 7;
public int numOfWays(int n) {
//第一行的两种类型
long aba = 6;
long abc = 6;
for(int i = 1; i < n; i++){
long aba2 = (aba * 3 + abc * 2) % MOD;
long abc2 = (aba * 2 + abc * 2) % MOD;
aba = aba2;
abc = abc2;
}
return (int)((aba + abc) % MOD);
}
}
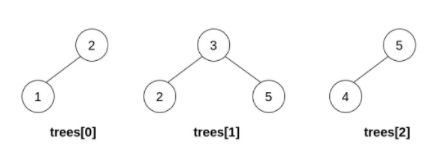
5810. 合并多棵二叉搜索树
题目描述
给你 n 个 二叉搜索树的根节点 ,存储在数组 trees 中(下标从 0 开始),对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ,且不存在值相同的两个根节点。在一步操作中,将会完成下述步骤:
选择两个 不同的 下标 i 和 j ,要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
用 trees[j] 替换 trees[i] 中的那个叶节点。
从 trees 中移除 trees[j] 。
如果在执行 n - 1 次操作后,能形成一棵有效的二叉搜索树,则返回结果二叉树的 根节点 ;如果无法构造一棵有效的二叉搜索树,返回 null 。
二叉搜索树是一种二叉树,且树中每个节点均满足下述属性:
任意节点的左子树中的值都 严格小于 此节点的值。
任意节点的右子树中的值都 严格大于 此节点的值。
叶节点是不含子节点的节点。
输入:trees = [[2,1],[3,2,5],[5,4]]
输出:[3,2,5,1,null,4]
解释:
第一步操作中,选出 i=1 和 j=0 ,并将 trees[0] 合并到 trees[1] 中。
删除 trees[0] ,trees = [[3,2,5,1],[5,4]] 。

在第二步操作中,选出 i=0 和 j=1 ,将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ,trees = [[3,2,5,1,null,4]] 。
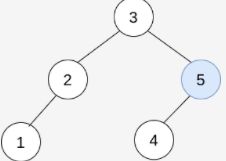
结果树如上图所示,为一棵有效的二叉搜索树,所以返回该树的根节点。
示例 2:

输入:trees = [[5,3,8],[3,2,6]]
输出:[]
解释:
选出 i=0 和 j=1 ,然后将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ,trees = [[5,3,8,2,6]] 。
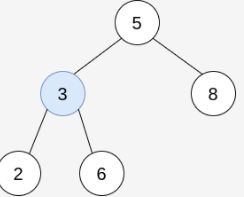
结果树如上图所示。仅能执行一次有效的操作,但结果树不是一棵有效的二叉搜索树,所以返回 null 。
示例 3:
输入:trees = [[5,4],[3]]
输出:[]
解释:无法执行任何操作。
示例 4:
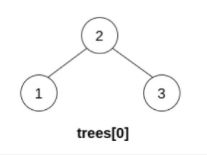
输入:trees = [[2,1,3]]
输出:[2,1,3]
解释:trees 中只有一棵树,且这棵树已经是一棵有效的二叉搜索树,所以返回该树的根节点。
提示:
n == trees.length
1 <= n <= 5 * 10^4
每棵树中节点数目在范围 [1, 3] 内。
trees 中不存在两棵树根节点值相同的情况。
输入中的所有树都是 有效的二叉树搜索树 。
1 <= TreeNode.val <= 5 * 10^4.
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/merge-bsts-to-create-single-bst
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
同样没看到题
看到这个题,感觉就是找相同的节点,但是一看数据范围,太多了
那么,怎么考虑呢
首先思考一个问题,这个最后形成的二叉搜索树的根节点是不是唯一的,显然应该是唯一的,因为答案是唯一的。
如果是唯一的话,那么这个根节点有没有和它相同的叶子节点?没有,如果有的话,根节点和叶节点相同,最后形成的树就不是二叉搜索树了。
那么可以遍历所有节点,根据这个条件找到这个根节点
然后对其他根节点进行替换,现在就自然而然想到一个问题,每个根节点能替换的叶节点是不是唯一的?因为每个根节点的值都是唯一的,如果用一个相同的点进行替换以后,还存在另一个相同的节点在最后的二叉搜索树中,那么这个树就不是二叉搜索树
所以得出结论,每个根节点能替换的节点也是唯一存在的
那么这个题就变成了找相同的点进行拼接,最后自然就形成了一个二叉树
最后检查形成的树是否是二叉搜索树同时包含了所给的全部节点
思路有了以后,代码写起来应该很快
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
Map<Integer, TreeNode> rootMap = new HashMap<>();
List<Integer> nodeValList = new ArrayList<>();
public TreeNode canMerge(List<TreeNode> trees) {
//特殊情况
if (trees.isEmpty()) {
return null;
}
//如果只有一棵树,那么直接返回
if (trees.size() == 1) {
return trees.get(0);
}
// 将根节点的值作为key,节点作为value放入rootMap
// 叶子节点的值放入leafSet
Set<Integer> leafSet = new HashSet<>();
// 遍历所有节点
for (TreeNode node : trees) {
int root = node.val;
// 有节点重复则不存在解,直接返回null
if (rootMap.containsKey(root)) {
return null;
}
rootMap.put(root, node);
TreeNode left = node.left;
if (left != null) {
// 有节点重复则不存在解,直接返回null
if (leafSet.contains(left.val)) {
return null;
}
leafSet.add(left.val);
}
TreeNode right = node.right;
if (right != null) {
// 有节点重复则不存在解,直接返回null
if (leafSet.contains(right.val)) {
return null;
}
leafSet.add(right.val);
}
}
// 寻找根节点,即在map中存在,但是在set中不存在
TreeNode rootNode = null;
for (int root : rootMap.keySet()) {
if (!leafSet.contains(root)) {
rootNode = rootMap.get(root);
break;
}
}
// 不存在根节点,返回null
if (rootNode == null) {
return null;
}
//将根节点移除,然后开始拼接
rootMap.remove(rootNode.val);
// 拼接rootNode,并判断所有节点都在rootNode下
dfs(rootNode);
//拼接完以后,如果map中还有点,那么说明没有全用上,返回null
if (!rootMap.isEmpty()) {
return null;
}
//判断拼接的二叉树是不是一颗搜索树
//中序遍历,判断得到的序列是否是递增的
inorder(rootNode);
for (int i = 1; i < nodeValList.size(); i++) {
//如果有不是递增的,那么直接返回null
if (nodeValList.get(i) <= nodeValList.get(i-1)) {
return null;
}
}
return rootNode;
}
public void dfs(TreeNode rootNode) {
//如何拼接,就是找到和rootNode左右节点相同的根节点,因为是唯一的,所以如果值相同就拼接
//先拼接左边
if (rootNode.left != null && rootMap.containsKey(rootNode.left.val)) {
rootNode.left = rootMap.get(rootNode.left.val);
rootMap.remove(rootNode.left.val);
dfs(rootNode.left);
}
//再拼接右边
if (rootNode.right != null && rootMap.containsKey(rootNode.right.val)) {
rootNode.right = rootMap.get(rootNode.right.val);
rootMap.remove(rootNode.right.val);
dfs(rootNode.right);
}
}
public void inorder(TreeNode treeNode) {
if(treeNode == null)
return;
inorder(treeNode.left);
nodeValList.add(treeNode.val);
inorder(treeNode.right);
}
}
总结
小结一下,这周两次比赛题官解都还挺难的,尤其是第三题,第四题没看到就不说了
感觉自己做的还是可以的,把自己能做出来的基本上都是一遍就AC了,稍微遗憾点的就是双周赛第二道题直接写BFS的话,可能第四道也有时间思考并且排名能更好一点
至于今天复盘学习到的东西,首先就是对动规有了更加深刻的认识,感觉动规是个无底洞啊。状态压缩很重要,和给的数据范围有很大关系。另外,动规还可以从前向后推。
还有就是迪杰斯特拉算法,下次不出意外的话应该可以自己手写出来。
收货颇丰,继续加油