论文精读：Neural Architecture Search without Training

1. Abstract

  手工设计深度神经网络所花费的时间和精力是巨大的，这推动了神经架构搜索(Neural Architecture Search，NAS)技术的发展，以实现自动化设计。然而，NAS算法往往速度慢且成本昂贵；它们需要训练大量的候选网络，以便为搜索过程提供信息。如果我们能够从网络的初始状态部分预测其训练的精度，这一问题就可以得到缓解。
  在这项工作中，作者测验了未经训练的网络中数据点之间的激活重叠，并激励如何能够给出有效表明网络训练性能的度量。作者将这种方法整合到一个简单的算法中，该算法允许我们在几秒钟内在单个GPU上搜索强大的网络，而无需任何训练，并在NAS-Bench-101、NAS-Bench-201、NATS Bench和NDS(Network Design Spaces)上验证了其有效性。
  最终，作者的算法能够在30s内在NAS-Bench-201搜索空间上搜索到精度为92.81%的网络，比传统NAS方法快了几个数量级。

  Paper：https://arxiv.org/abs/2006.04647
  Code：https://github.com/BayesWatch/nas-without-training

2. Background

Time	Paper	Author	Method	[Dis]advantages
2017	Neural architecture search with reinforcement learning	Zoph & Le	作者使用RNN控制器来生成候选网络，并对候选网络进行训练，使用强化学习更新控制器，以提高其生成的候选网络的质量	控制器每次的输出结构都要进行训练，成本较高，作者使用800个GPU在CIFAR10数据集上训练了28天；缺乏灵活性，最终获得的网络是固定的，不能扩展，即不能用于移动设备或其他数据集
2018	Learning transferable architectures for scalable image recognition	Zoph et al.	在神经单元块上搜索，而不是在整个架构上搜索。即作者搜索一个标准单元和一个简化单元（合并池）进行CIFAR10分类，然后将其用作ImageNet分类的更大网络的单元块	在数量上更加灵活，单元块可以根据预算进行调整；500个GPU训练了4天
2018	Efficient neural architecture search via parameter sharing	Pham et al.	允许候选网络共享权重，以便进行联合训练	降低了搜索的计算成本，使用单个GPU在CIFAR10数据集上运行了半天
2020	Evaluating the search phase of neural architecture search	Yu et al.	证明了共享权重方法抑制了对最佳网络结构的搜索，使随机搜索成为一种极其有效的NAS基线	/

  对于一些从业者来说，NAS仍然很慢。在硬件感知设置中，能够快速（即以秒为单位）执行NAS将非常有用，在该设置中，每个设备和任务通常需要单独搜索。

Time	Paper	Author	Method	[Dis]advantages
2019	FBNet: Hardwareaware efficient convnet design via differentiable neural architecture search	Wu et al.	/	/
2019	MnasNet: Platform-aware neural architecture search for mobile	Tan et al.	/	/

  评估NAS算法有效性的主要障碍是搜索空间（所有可能网络的集合）太大，无法进行详尽的评估。下面介绍几个常用的benchmarks：

Benchmarks	Introduction
NAS-Bench 101	包含423624个神经网络，在CIFAR10数据集上经过了108个epoch的训练，使用了三种不同的初始化
NAS-Bench 201	包含15625个神经网络，CIFAR10/CIFAR100/ImageNet-16-120数据集上训练了多次
NATS-Bench	有两种搜索空间：拓扑搜索空间NATS-Bench TSS，包含15625个神经网络，也就是NAS-Bench 201；大小搜索空间NATS-Bench SSS，包含32768个神经网络，这些网络之间的cells通道数不同。

3. Method

3.1 score

  作者的目标是设计一种方法，在初始化时对网络架构进行评分，以表示其最终训练的精度，这样就可以使用成本低廉的计算方法来代替NAS算法中昂贵的训练步骤。
  给定一个具有修正线性单元(rectified linear units, RELU)的神经网络，我们可以在每层的每个RELU单元上确定一个关于该单元是未激活（值为负，因此乘以零）还是已激活（在这种情况下，其值乘以一）的二进制指标。固定这些指标变量，现在网络由线性算子局部定义，该算子通过将散布在每个层上的线性映射(the linear maps)与二进制校正单元(the binary rectification units)相乘而获得。
  mini-batch data $X=\{x_i{\}}_{i=1}^N$可以通过神经网络映射为$f(x_i)$，$f$中$x$处RELU单元的指示变量形成一个定义线性区域(the linear region)的二进制码$c_i$。与两个输入相关联的二进制码越相似，网络学习分离这些输入就越具有挑战性，当两个输入具有相同的二进制码时，它们位于网络的相同线性区域内，因此特别难以分离。相反，当输入被很好地区分时，学习应该更容易。下图可视化了ReLU单元的二进制激活码对应的线性区域：

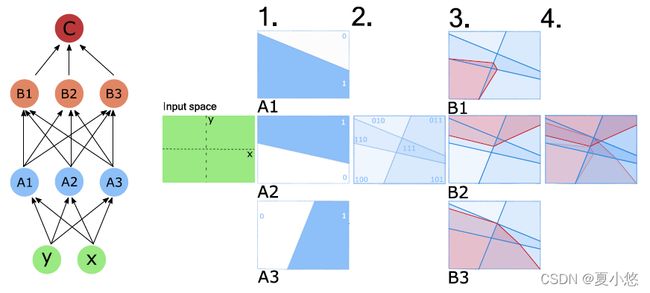
  其中，1. 每个ReLU节点$A_i$将输入拆分为激活区域(>0)和非激活区域，我们将激活区域标记为1，非激活区域标记为0；2. 与每个节点$A_i$相关联的激活和非激活区域相交，具有相同激活模式的输入空间(input space)区域是共线的(co-linear)；3. 下一层的ReLU节点$B$将空间进一步划分为激活区域和非激活区域；4. 给定节点上的每个线性区域都可以由其前面的所有ReLU节点的激活模式唯一定义。
  作者用汉明距离(Hamming distance) $d_H(c_i,c_j)$来衡量两个输入（未训练网络的输入二进制码）的不相似程度(也可以说是相似性程度)，因此可以通过计算核矩阵(kernel matrix)$K_H$来测验整个小批量数据的二进制码之间的对应关系：
$$K_H=\left(\begin{array}{ccc}{N}_A-d_H(c_1,c_1)& \dots & N_A-d_H(c_1,c_N)\\ ⋮& \ddots & ⋮\\ N_A-d_H(c_N,c_1)& \dots & N_A-d_H(c_N,c_N)\end{array}\right)$$  其中，$N_A$是网络中RELU单元的数量，$N$是mini-batch的大小，这里是128。

  这一点理解有些别扭，核矩阵$K_H$衡量的是不同数据输入的相似性程度，相似性程度越低，$K_H$越接近于对角线。

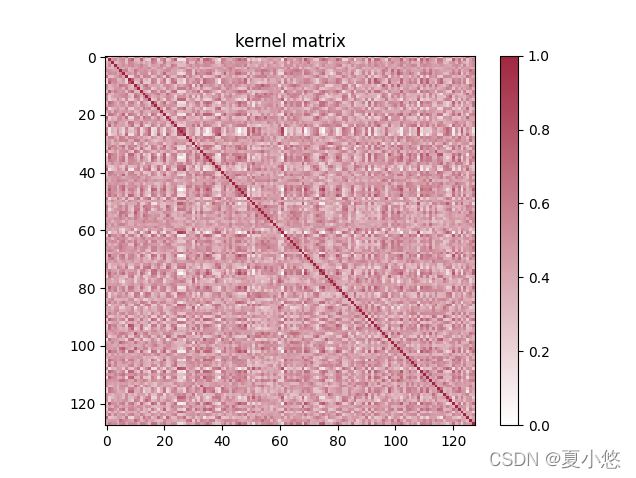
  高性能网络具有较少的非对角元素和较高的相似性（如下图），可以利用这一观察结果来预测未经训练的网络的最终性能，作者使用以下公式来评估模型的性能：
$$s=log|K_H|$$  $K_H$越接近于对角线(最好只有对角线，也就是相似性越低，即不相似性越高)，$s$越高，表示训练后的模型精度更高。

  举个简单的栗子：
    假设$K_H=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$，则$|K_H|=\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$，当b=c=0时，$|K_H|$有最大值，即$K_H=\left(\begin{array}{cc}a& 0\\ 0& d\end{array}\right)$，此时$K_H$是一个对角矩阵，也就是只有主对角线元素有值，其它位置均为0。此时的$K_H$表示的相似性程度最低，相应的$score$最高。

  上图显示的是NAS-Bench-201中未训练的网络结构对应的核矩阵，输入的mini-batch size为128。将这些图中的$K_H$归一化，以便对角线条目为1，然后根据最终的CIFAR10验证精度将$K_H$分类为列。较暗的区域具有较高的相似性，轮廓鲜明，精度低；较浅的区域相似性很小，模型的精度高，说明模型能够很好的区分图像的特征，因此可以使用$K_H$来预测未经训练的网络的最终性能，而无需任何训练。

  Hamming距离：对应二进制位不同的位置的数目

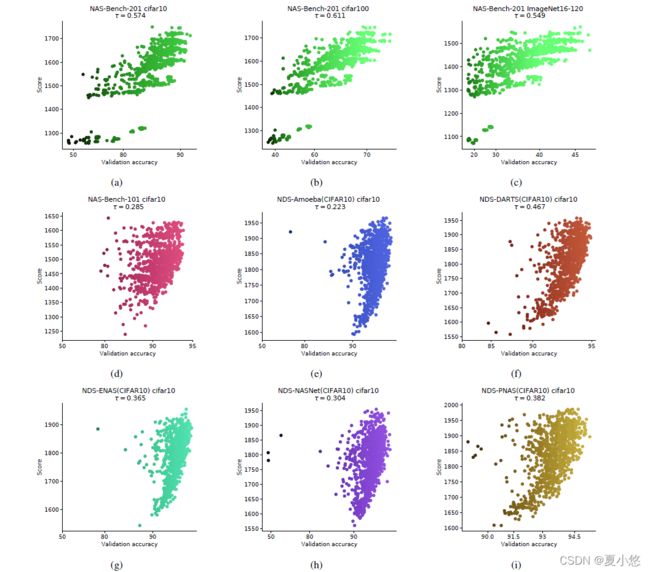
  为了说明score与模型精度的关系，作者对比了各搜索空间在各数据集上的score与模型的精度(随机采样1000个样本)，可以看到模型的精度与score有一定的线性关系，具体如下图：

  其中，$\tau$表示Kendall系数。

3.2 NASWOT

  作者提出了一种NASWOT(Neural Architecture Search without Training)算法（如下图），即不使用神经网络作为生成器，而是从搜索空间中随机生成一个候选网络，然后使用score方程在未经训练的状态下对其进行评分。

3.3 AREA

  作者提出的score可以直接并入现有的NAS算法中，为了证明这一点，作者在REA(Regularised EA)上进行了改变，称之为AREA(Assisted-REA)。AREA随机抽样一个更大的群体(population为20，REA为10)，并使用score为REA算法选择初始群体，具体算法如下：

4. Experiments

  作者使用了CIFAR-10、CIFAR-100和ImageNet-16-120数据集在NAS-Bench-201搜索空间上对非权重共享、权重共享和免训练三种方法进行了对比，无能论是搜索速度，还是搜索出来的模型精度，其性能都比其他方法好，尤其是搜索速度，比其它的NAS算法快了几个数量级。具体如下图：

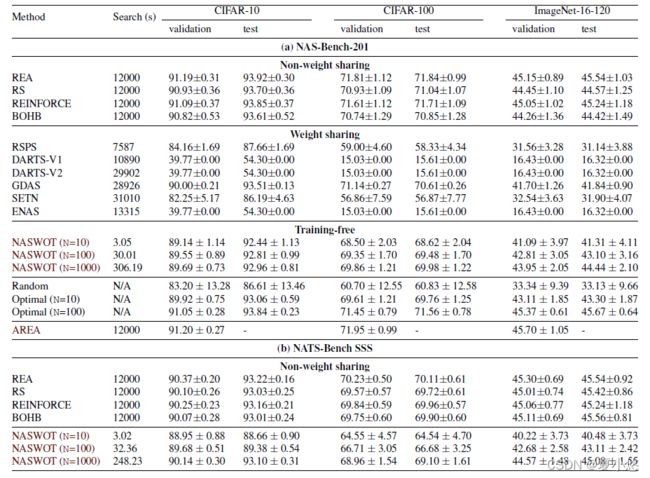
  此外，作者在CIFAR-10数据集上，对自己的算法和其他NAS算法在搜索时间和精度上做了一个更直观的比较，具体如下图：

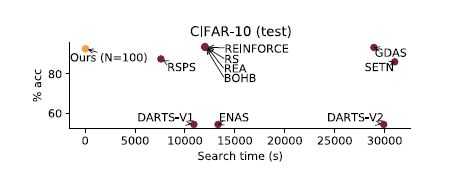
5. Core code

  根据代码，作者的核矩阵可以理解为一个混淆矩阵，表示的是数据的相似程度。

# 核矩阵kernel matrix
inp = inp.view(inp.size(0), -1)
x = (inp > 0).float()
K = x @ x.t()
K2 = (1.-x) @ (1.-x.t())
network.K = network.K + K.cpu().numpy() + K2.cpu().numpy()
"""K表示了二进制码中相同位置的个数，network.K表示的是整个网络的二进制码中相同位置的个数，也就是相似度"""

  为了方便展示，这里小编也将核矩阵进行了可视化操作，具体如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm, colors


def plot_confusion_matrix(data, title, cmap):
    data_max = data.max()
    data_min = data.min()
    data = (data - data_min) / (data_max - data_min)
    plt.imshow(data, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar(cm.ScalarMappable(cmap=cmap))


if __name__ == '__main__':
	data = np.random.randn(128, 1000)
	x = np.zeros(shape=data.shape)
	x[data > 0] = 1
	k1 = x @ x.T
	k2 = (1 - x) @ (1 - x.T)
	k = k1 + k2
	
	cmap = colors.LinearSegmentedColormap.from_list('cmap', ['#FFFFFF', '#A12741'], 256)
	plot_confusion_matrix(data=k, title="kernel matrix", cmap=cmap)
	# plt.savefig('kernel-matrix.png')
	plt.show()

  根据源代码实际的核矩阵，对其进行了可视化操作，效果如下：

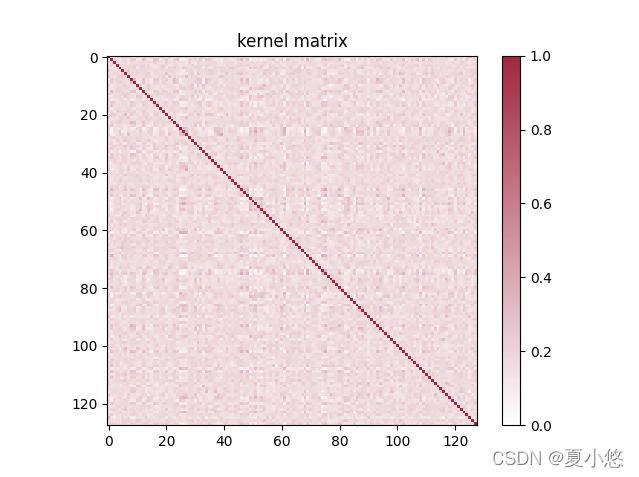
  score的计算也很简单，使用了numpy.linalg库来计算：

def hooklogdet(K, labels=None):
	# 计算行列式的符号和自然对数
    s, ld = np.linalg.slogdet(K)
    return ld

  Kendall系数$\tau$的计算：

from scipy import stats

tau, p = stats.kendalltau(accs_[:max(i-numnan, 1)], scores_[:max(i-numnan, 1)])

  代码中还计算了Jacobian行列式，但没用到：

def get_batch_jacobian(net, x, target, device, args=None):
    net.zero_grad()
    x.requires_grad_(True)
    y, out = net(x)
    y.backward(torch.ones_like(y))
    jacob = x.grad.detach()
    return jacob, target.detach(), y.detach(), out.detach()

  Jacobian行列式，即雅可比行列式，不严谨地说就是由函数的一阶偏微分组成的方阵。