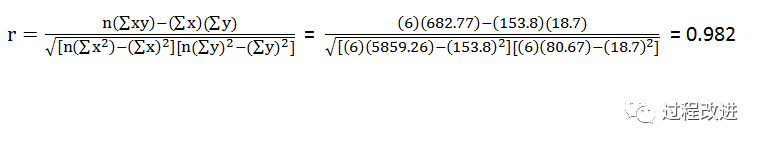MA1 轻轻松松学统计分析（下）

分析：从蚕豆实验到6年销售数据

第二天，孩子乖乖地来找我，他说：“爸爸，今天我跟老师说了你的工作是做统计分析，老师听到后就发给我一些高年级的生物实验数据，希望帮他做些分析，看看两类实验结果有没有差异。你可以帮忙吗？”

蚕豆植物-双样本t-test

以下数据显示了某一化学物质在蚕豆10个剪枝植株和10个生根植株中的(比例)浓度。
有根:53 58 48 18 55 42 50 47 51 45
剪枝:36 33 40 43 25 38 41 46 34 29
 

我说:你可以同样用昨天学过的方法（如，柱状图）比较两组数。
孩子就按这个汇总了两个实验数据的分布，如下图所示：

我看了一下，说：“这个你应该也看得懂：上面那个实验数据有一个很明显的异常点——18。你应该要问老师，这个18是错误数据还是一个值得相信的数？如果18是不对的，很明显地，你能发现第一个实验中的平均浓度比下面高……”。当然，还有很多数据，并没有这么简单，我们就可以用一个叫“双样本t”的检验方式来比较两种数据是否有显著差异。但是如果有刚刚那种异常点，如直接用双样本 t 分析，因为第一组数据被那个18拉低了，结果很可能是两组没有显著差异。所以还是直接看数据的分布更实在。

我就给他总结一下：我们在统计学可以使用假设检验，其中包括双样本t检验比较,方差分析(ANOVA)等[详见附件A1,A2]，就是针对这类统计数据分析。但是针对这个实验的数据，你从统计图一眼就能看出有显著区分，就不需要再采用这些假设检验方法，因为采用那些技巧不会得出额外的信息。

我接着跟他说:有些时候统计数据不是连续数据，像学生成绩、浓度、高度等，而是分组数据。例如下面这些国外人种眼睛颜色与头发颜色的数据，这种数据我们就需要用列联表 (Contingency Table) 来看这两个分组的变量之间有没有关系。

头发和眼睛颜色的不同组合

592人的头发和眼睛颜色的不同组合：

B4表	Hair colour头发颜色
Eye colour眼睛颜色	Black黑	Brunette深褐	Red红	Blond金
Brown棕	68	119	26	7
Blue蓝	20	84	17	94
Hazel淡绿褐	15	54	14	10
Green绿	5	29	14	16

如果我们对上面 B4 表的数，加上每一行、每一列的总和，得出下面 B5 表，我们从每一列可看见，除了金发 (blond)那列例外，棕色(brown)眼睛的占大多（金发的大部分是蓝(blue)眼睛）。也看到金头发那列跟其他，如黑头发那列，分布不一样。比如我们看每行的话，也可以看到棕色眼睛跟蓝眼睛的数量差不多都是最多。但它们在金头发(blond)和黑头发(black)那列的分布就完全不同。统计分析的卡方检验[详见附件A3]也可以帮我们分析分组数据间有没有相关。但是像这类简单的4 X 4 数据表，只要计算出如B7表所示的列联表已经可以帮我们看到实际金发蓝眼睛数比预计多，反过来，实际金发棕眼睛数比预计少，卡方检验只告诉我们眼睛颜色与头发颜色之间有关，但其实我们在前面看B5 B7 已经知道，卡方检验没有带来额外有用信息。

实际(Obs.) 数量表:

B5表	Hair colour头发颜色
Eye colour眼睛颜色	Black黑	Brunette深褐	Red红	Blond金	Total
Brown棕	68	119	26	7	220
Blue蓝	20	84	17	94	215
Hazel淡绿褐	15	54	14	10	93
Green绿	5	29	14	16	64
Total	108	286	71	127	592

实际(Obs.) vs 预计(Exp.)列联表 Contingency Table:

B7表	Hair colour头发颜色
	Black黑		Brunette深褐		Red红		Blond金
Eye colour眼睛颜色	Obs.	Exp.	Obs.	Exp.	Obs.	Exp.	Obs.	Exp.	Total
Brown棕	68	40	119	106	26	26	7	47	220
Blue蓝	20	39	84	104	17	26	94	46	215
Hazel淡绿褐	15	17	54	45	14	11	10	20	93
Green绿	5	12	29	31	14	8	16	14	64
Total	108		286		71		127		592

销售数据——多元回归

表C.1显示了某原料六年来的销售额、每吨平均价格和广告支出的情况。找出销售额与单价、广告费之间的回归关系，并评价这些回归方程式。这些方程式能否表达价格水平和广告支出对销售的影响?你能想出另一种总结数据的方法吗?

表C.1	1979	1980	1981	1982	1983	1984	Average平均值
Sales销售( ￡million百万英镑),S	250	340	300	200	290	360	290
Price价格( ￡英镑),P	25	48	44	20	38	60	39
Advertising广告费( ￡’000 ),A	35	32	38	30	34	46	36

二元回归方程

你可以立马使用统计分析工具，求出二元回归方程 [详见附件A4]：
S = 4.26P - 1.48A + 176 , R2 =0.955

你觉得这条回归方程式有用吗？没用。
首先不应该只用六个点来求一条二元回归方程，数据不够，所以我们更要了解这种回归方程式的局限：这个例子也让我们可以看到两个相关因子产生的问题，例如：假设 P保持不变，增加 A， S应该会升，但以上的二元回归方程反而预测 S会下降。

所以- 1.48A（负数）不太合理，在二元回归中，因为因子之间相互影响，不能像单因子一元回归，可以这么简单地看参数正负。

应该怎么分析？
应从基本步骤开始， 当X Y都是连续数据，可先用散点图画出X Y之间的关系。对 S 和 P 也画散点图，看关系；然后 S 和 A ；P 与 A 之间也要看。从这三个散点图可以看出S 和 P 有关系 A一直都比较稳定，但到最后一年，P和 A都升了很多 ， S 也升。

一元回归方程

得出 S与P的线性关系方程式：S = 140 + 3.84 P , R2 = 0.946

(R2越大代表这条线越能代表这些点，最高是1，代表这些点都在这条直线上面。)

同样对 S 与 A 做回归分析，但得出 R2 = 0.437 ，表示关系较弱。所以就不用 A，只利用 P 求回归方程。

也可以 换个思路，用 V = S / P

得出 V与P的线性关系方程式：
V = 12.2 - 0.11 P , R2=0.932

回归分析的注意事项

注意： 我们可否利用以上回归方程来预测未来销售额？ 不可以，尤其是如果广告预算有显著变化。因我们计算回归方程时，没有利用广告费建模。（总共才六组数据也太少） 问：下一步应如何完善回归分析？ 答： 要先了解公司的广告预算策略， 例如，很多公司广告费是按销售的固定比例。但也可能因为怕销售额下降，增加广告预算。了解后，便可以加入其他影响因素（如，广告），然后再多收集数据并分析。

其他注意事项：

• 不能直接延伸，公式预测有适用范围

• 不应直接求公式，要先看看散点图关系

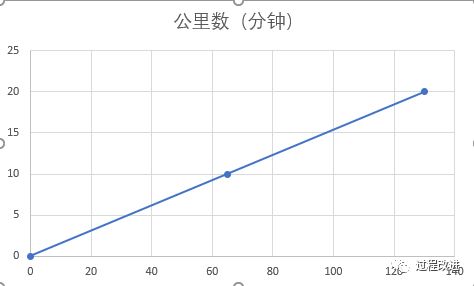
直线延伸 Extrapolation

上图是某业余长跑手的统计，可以看到跑20公里用130分钟，形成一条直线（每6分半一公里），但我们不能利用这条直线推论他跑30公里的时间是10公里的3倍，甚至全马（40KM）时间是10公里的4倍。因为后期会因为体力不足而越来越慢。肯定不是一条直线，估计应是弧线，但弧度多少必须有他到40公里的数据才能得知。 那么以前的历史数据就没有什么用吗？也不是，以往到20公里的数据可作为参考，只是不能简单当成直线延伸。

使用回归方程也一样，只能适用于有数据支持的范围。

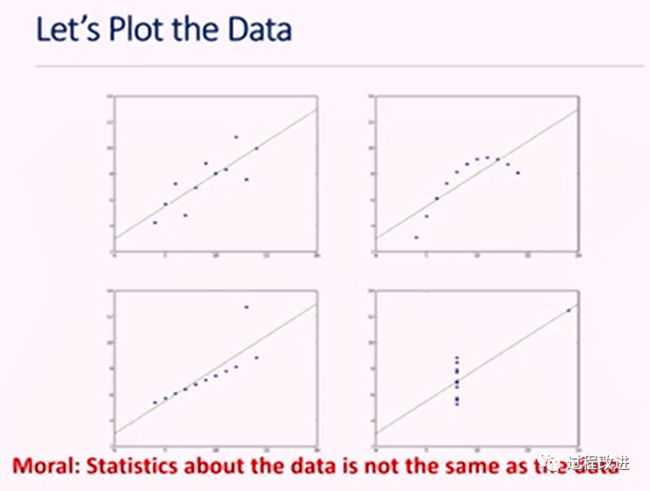
4组数据的回归方程

有下面四组XY，每组11对数据，回归方程(甚至X或Y的平均偏差)都一样，但是如果我们把每组数据生成散点图看，便看出，除了第一组数据，其他三组都不能用直线回归分析。 以上是1973年统计学家发表的例子，所以我们不应盲目地输入一堆数字，一键求出回归方程,便以为得出回归方程式和相关指数便完事，必需先画出数据的散点图，看看两个变量的关系。

总结

上篇主要讲如何描述数据，这篇主要介绍数据分析，与解读(Interpret) , 例如：

分析方法	这篇实例
双样本t-test	蚕豆实验
卡方检验与列联表t	头发和眼睛颜色的不同组合
回归分析	原料销售

虽然计算机可以帮我们很快地分析数据，得出结论或者方程式，但也导致我们忽略了统计分析的根本：

• 先了解问题与背景，明确目标

• 确保收集数据的质量

• 初步数据分析

所以在我们对两组蚕豆实验（有根,剪枝）数据做t-test之前，应该先看看两组数据的分布图。
做卡方检验之前更重要是先利用列联表 (Contingency Table)，看看眼色与发色之间有什么关系。
做回归分析之前， 必须先画散点图，看看两个变量之间的关系。

不要轻视上篇的数据描述性分析。

后记

去年一位小学生家长问：老师，你觉得小学生学编程有用吗？
答：小学生更重要是学数学，编程是辅助的工具。我是60后，初中时代还没有计算器，数学老师还给我们介绍他们那个时代怎么用计算尺(slide rule)来把两个数相乘。现代恰恰相反，问一个学生，1228+356 =？他立马就去打开手机计算器。在我那年代，都能直接用心算算出是 1584。统计分析也有同样的问题,正因为现在电脑软件太普遍，很多人一看见一堆数字，不先画图来看看分布，直接就套工具求方程式关系。从前面那些例子可以看到，这种只求方程式的思路很危险，因为很多假定可能不对，导致出来的结论错误、无效。

与项目经理一起分析敏捷迭代数据 十多年前，刚拿到六西格玛黑带， 我会首先把数据输入电脑、用工具分析，看数据之间有什么关系。 现在，当客户从6至8个敏捷迭代项目中，收集了6 -8轮数据， 首先我问他们数据是如何收集？是否可靠？然后会直接在白板上用水笔把各数据按每迭代，用不同颜色代表不同组，手画出每个项目的趋势，与他们项目经理一起讨论、判断，例如：数据范围是多少，是否稳定，需不需要细分...…  因数据量少，完全不需要用统计分析工具，大家一起看白板讨论效果更好。

美国软件工程顾问Gerald M WEINBERG 先生说过,“如果你的数据分析需要超过初中程度的话，你要想想这种分析是否有效？”

在CMMI高成熟度咨询时，常常有人问：我们在CMMI不是要求高层也用统计分析来管理吗？如何实现？
我这样解读：公司要做到高成熟度，不可能要求每个员工，包括高层都是六西格玛黑带、统计学博士。可能有些详细的分析需要很多统计的技巧，但是分析员最终要用一些老板听得懂的方式把那些结果分析出来，让他看得懂。但我看很多公司的统计分析员，只是沉迷于大数据，深度学习、AI等“高级”方法，以为无论什么数据，都可以使用统计分析，得出X-Y的关系方程式，反而忽略了一些基本道理:
如果你可以把你的分析结果跟你的孩子说得清，这种统计分析才算有效。

下篇分享统计分析如何用于软件开发管理，以数据说话，解决问题。

反馈

杭州高级经理：
这一篇很有意思，因为我是学经济的，统计学也是必修的一门学科，我在学习这门学科时，觉得是有点难度；但看了您写的这篇文章后觉得统计学其实还是蛮有乐趣，并且很实用，而且还可以运用到项目管理中去，让我大受启发！谢谢宋老师，每次学习您的文章，我总能学习到新的内容，受益匪浅

一位香港资深经理：
统计学真正发扬光大的时刻是二次大战，而应用得最多和可能最好的是在美国。当时美国利用留在本土的女性到工厂生产炮弹和子弹，他们利用统计学去测试每一批次生产的子弹质量，这是用来保障每粒子弹在枪膛中都能成为发射，不卡者、滑出、不爆等情况。同样的统计学方法就应用在生产管理上，相信这会对小孩引起兴趣。这也是提升和释放强大生产力。

杭州资深经理：
看了你的文章，我终于能理解您在我们CMMI5 的辅导和评估过程中反复强调的观念:

• 数据是用于分析的，一定要了解背景，基于什么目的，采集什么样的数据，做什么样的分析，用什么工具分析

• 并不是所有用工具跑出来的结果就是正确的，有些数据还是要经过人工筛选和处理，才有实际的意义

• 能用简单的方法，尽量不要把事情搞复杂 —— 这点特别受用

附件

A1: 2-sample T test

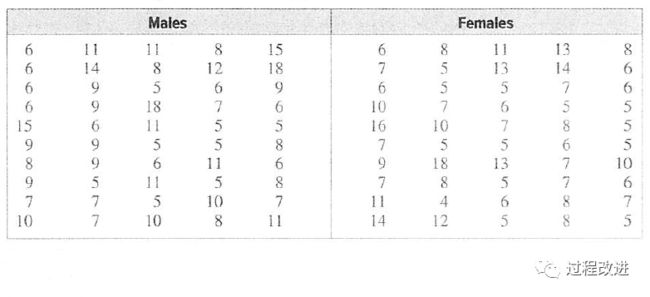
例：大学体育活动

假设:大学为男生提供的运动项目的平均数量大于为女生提供的，下面是随机抽样美国各大学为男女生提供的体育项目量，如果Alpha*=0.10，检验男女是否有显著差别。（假定，男女生数据的标准差都一样 δ1=δ2 = 3.3）

 * Alpha（显著性水平) 是指当零假定是真，但被拒绝的错误率。（也称为第I类错误） 

置信区间(Confidence interval) = 1 - alpha

Minitab

检验两个独立样本平均值之间是否有显著差异
零假设 - 两者没有显著差异

先看看两组的柱状图 （minitab)：

1. 统计-基本统计量-双样本T(2)

由于p值大于显著性水平，0.172> 0.05，所以不能拒绝零假设 - 两者没有显著差异。

A2: ANOVA

示例12-1每加仑汽油行驶

研究人员想看看三种不同类型的汽车:小型汽车（small）、轿车(sedans)和豪华汽车(luxury)在城市驾驶时的燃油经济性是否有差异。他随机抽样了四种小型汽车、五种轿车和三种豪华汽车。每加仑的英里数都都在下面列出。在α= 0.05时，检验三种平均值之间是否没有显著差异。[Source: US Environmental Protection Agency]

ANOVA 例子

1:零假设:三种不同类型的汽车:小型汽车、轿车和豪华汽车在城市驾驶时的燃油经济性平均值之间没有差异
2:也可用统计工具 Minitab 做 ANOVA分析，并算出P值=0.038 低于0.05 ，所以拒绝零假设， 三类有显著差异

minitab

统计-方差分析-单因子（未堆叠存放）

A3: 卡方检验与列联表 Contingency table

一位研究人员希望了解医院和病人感染的数量之间是否有关系。我们随机抽取了3家医院，并报告了特定年份的感染人数。数据如下。

Hospital医院	Surgical site infections手术部位感染	Pneumonia infections肺炎感染	Bloodstream infections血行感染	Total合计
A	41 （50.30）	27 (27.81)	51 (40.89)	119
B	36（33.39）	3（18.46）	40（27.15）	79
C	169（162.31）	106（89.73）	109 （131.96）	384
Total	246	136	200	582

卡方检验例子

1:零假设:医院(Hospitals) 与 感染种类(Infections) 之间没有相关

2：Degree of Freedom(DF)=(3-1)×(3-1)=4,从卡方参考列表,α=0.05对应的卡方关键值是9.488

3:首先使用以下公式计算每个列联表的预计值E(Expected Value)，得出E写在（）中

再用下面公式从预计值与实际值O(Observed value),计算卡方值 ：

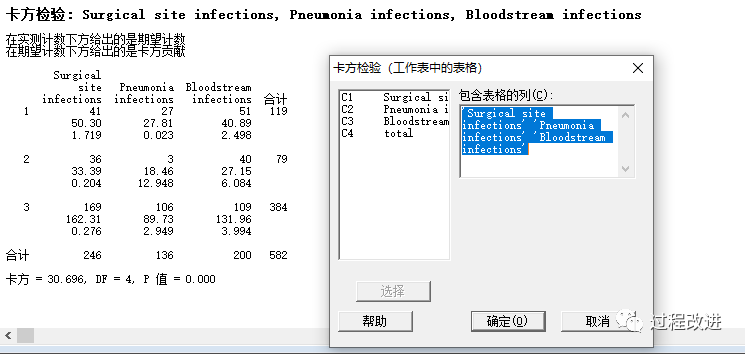
4:得出卡方=30.7 ，比预估关键值（9.488）高，所以拒绝零假设，医院(Hospitals) 与 感染种类(Infections) 之间相关

也可用统计工具 Minitab 得出卡方，算出P值低于0.05 ，所以拒绝零假设 :
统计-表格-卡方检验（工作表中双向表）

A4: Linear Regression

回归分析希望找出一条直线，它与每个点的距离的平方总和最小。

该如何做回归分析？

• 如果使用电脑程序，通过“最小二乘法”计算并绘制这条线。

1. 计算相关系数R,使用下面的方程式。

2. 通过使用方程式y=mx+b,确定斜率或线的y轴截距。

• y截距是“最佳拟合线”穿过的在y轴上的点（在这一点，x=0）。

• 线的斜率（m）按照y的变化除以x的变化来计算（m=∆y/∆x）。斜率m也认作预测变量x的系数。

•  R2衡量回归方程能多好代表这些点，最理想状态， R2等于1，表示零误差，所有的点都在回归线上。

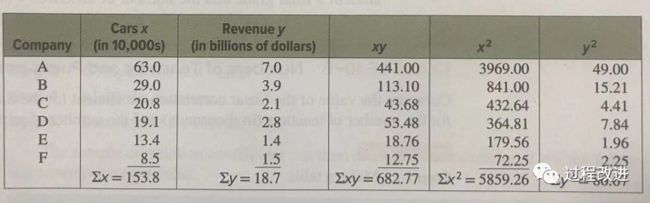
例10-1汽车租赁公司

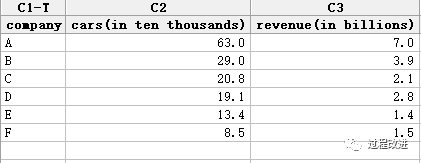
以下为美国随机抽样六家汽车租赁公司最近一年的总收入（亿美元）。

解决方法

• 绘制散点图，如图10-2所示

• 确定是否存在关系。发现代理商拥有的汽车数量和公司的总收入之间似乎存在正线性关系。

• 代入公式，计算出R

结论：汽车租赁公司的汽车数量和它的年销售额之间有很强的正相关关系，也就是说，汽车租赁公司拥有的汽车越多，公司的年销售额就越多

也可以用 minitab

图形-散点图（回归分析）

也得出 R2 = 96.4% , 调整后 = 95.5%
Revenue (年销售额) = 0.396 + 0.106 x Cars (汽车数量)

References

1. GUTTAG, John V.: "Introduction to computation and programming using Python" MIT Press 2021
2. CHATFIELD, Chris : "Problem Solving: a statistician's guide 2/e" Chapman & Hall 1995
3. BLUMAN: Elementary Statistics 10/e