到目前为止,我们一直都在讨论有限状态下的MDP问题,现在我们来看下当状态数量是无限时如何求解MDP问题。
离散化
也许求解无限状态下的MDP问题最简单的方法就是先将无限状态离散化成有限状态,然后再用之前介绍的价值迭代或者策略迭代算法了。
假设我们有两个状态s1和s2,我们可以用下图所示的网格来离散化这个状态空间。
图中的每一个网格都代表独立的离散状态s*,因此我们可以把无限状态的MDP近似表示成(S*, A, {Ps*a}, γ, R),其中S*是所有离散状态的集合,{Ps*a}是在状态s*采取行动a的概率分布。然后我们就可以用价值迭代或者策略迭代算法求出V*(s*)和π*(s*)。
离散化的方法可以在很多场景都有很好的应用,但是它也有两个明显的缺点。第一个缺点是离散化只是对连续状态的近似,有时会有很大的误差。
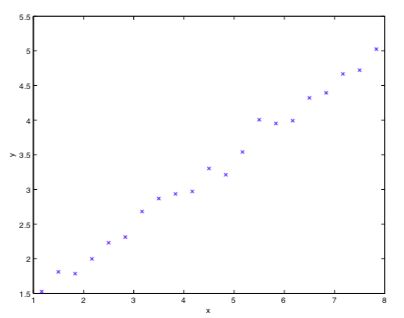
为了更好地理解这一点,考虑如下的监督学习问题:
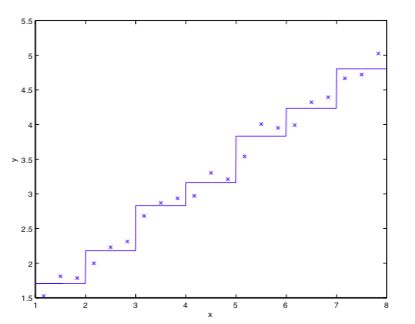
如果我们用线性回归作拟合,那么拟合效果是很好的。但是如果我们用离散化的方法去作拟合,那么拟合效果就如下图所示:
离散化的方法无法精确表示光滑曲线,如果需要降低误差,那么需要将离散化的粒度变得更小。
离散化的第二个缺点被称为维度的诅咒(curse of dimensionality)。假设我们把n维状态空间离散化成k份,那么所有离散状态的总数是kn个。当n值变大时,所有离散状态的总数呈指数性增长。比如当n=10,k=100时,所有离散状态的总数是10010 = 1020个,这个数字对于现在的计算机来说也是很难处理过来的。
作为一个经验法则,离散化通常对1维或2维状态的问题有较好的效果。如果处理得当,离散化也能很好处理4维状态。在极端情况下,离散化最多能处理到6维状态。一旦维数超过6,那么离散化将很难发挥出作用。
价值函数近似
现在我们介绍另一种求解无限状态下MDP问题的方法,这次我们来直接估计V*。这个方法叫做价值函数近似(value function approximation),在强化学习问题中有着成功的应用。
使用模型
在价值函数近似算法中,我们需要训练一个模型(model),也称为模拟器(simulator)。简单来说,模拟器就是一个黑箱,它的输入是任意状态st和行动at,输出是根据状态转换概率Pstat得到的下一个状态st+1。
我们可以有多种方法获得这个模型。一种方法是通过物理模拟,比如我们可以通过物理定律和已知参数进行推导,或者使用现成的物理模拟软件进行建模。
另一种获得模型的方法从MDP的训练数据中进行学习。比如我们进行m次MDP的试验(trial),每次试验进行T个时间序列步骤。这样我们就得到了如下m次试验数据:
我们可以将st+1看成是一个以st和at为参数的函数,然后通过某个学习算法求得该函数。
比如我们可以选择如下的线性模型:
通过线性回归的算法可以求得模型中的参数,也就是A和B两个矩阵。通过最大似然估计法,可以求得参数为:
求出A和B两个参数后,一种方法是建立一个确定(deterministic)模型,也就是通过等式(5)给定参数st和at来唯一确定st+1。另一种方法是建立一个随机(stochastic)模型,也就是说st+1是关于输入的一个随机函数,这个模型可以表示为:
其中εt是噪音项,通常来说εt ~ N(0, Σ)。
上面我们假设st+1是关于当前状态和行动的线型函数,但在实际情况中,非线性函数也是有可能的。这时我们可以把模型表示为:
其中φs和φa是关于状态和行动的某个非线性函数。另外我们也可以使用非线性学习算法,比如局部加权线性回归算法来估计参数。上述方法在构建MDP的确定模型和随机模型中都适用。
拟合的价值迭代
现在我们介绍拟合价值迭代(fitted value iteration)算法,它同样用于求解无限状态下的MDP问题。这里我们假设连续状态空间S = Rn,行动空间A规模很小且是离散的。
回顾一下在价值迭代算法中,我们每次都是在更新:
注意,由于现在状态空间是连续的,所以这里用积分的方式来替代求和。
拟合价值迭代的中心思想是通过某个监督学习算法(这里我们用线性回归)来近似求出价值函数,其中价值函数是关于状态的线性或非线性函数,可以用下式表示:
其中φ是关于状态的某个映射函数。算法步骤描述如下:
算法的每次循环中,首先每次取样出k个状态,然后计算出y(i),这个值正是对V(s)的近似(等式7的右边)。最后通过应用监督学习算法(线性回归)使得V(s)与y(i)尽可能的接近。
和有限状态的价值迭代算法不同,拟合价值迭代并不能保证算法总是收敛的。然而在实际应用中,算法通常是收敛的。注意,如果我们使用上一小节介绍的确定性的模型,那么价值迭代算法可以通过令k=1的方式进行简化。
最后,拟合价值迭代算法输出的是V,这是对V*的近似。特别地,当系统处于某个状态s时,我们需要选择一个行动,这个行动a将会是:
计算这个值的过程和拟合价值迭代算法的内层循环很相似。
总结
- 无限状态下MDP问题可以通过两个算法求解:离散化和价值函数近似
- 离散化通常对2维以下状态的问题有较好的效果,极端情况下最多适用于6维以下状态
- 价值函数近似又可分为两种:使用模型和拟合价值迭代,其思想在于通过某种方法(物理模拟或算法学习)求得价值函数的一个近似值
参考资料
- 斯坦福大学机器学习课CS229讲义 Reinforcement Learning and Control
- 网易公开课:机器学习课程 双语字幕视频