Kotlin 用列表处理数据
文章目录
- 1. Kotlin 有哪些可用的列表
-
- 1.1 使用持久数据结构
- 1.2 实现不可变的、持久的单链表
- 2. 列表操作中的数据共享
-
- 2.1 使用递归对具有高阶函数的列表进行折叠
- 2.2 使用型变
- 2.3 创建 foldRight 的栈安全递归的版本
- 3. 小结
1. Kotlin 有哪些可用的列表
Kotlin 提供 可变、不可变列表。 在 Java 中也支持,但是得益于 Kotlin 的扩展函数特性, 列表拥有了大量增强性能的函数。
- 可变列表
像 Java 列表一样,可以通过添加、插入或者删除元素来改变列表, 这样一来,列表的早期版本将会丢失 - 不可变列表
又称只读列表,不能被修改的列表。 如果向其添加一个元素,则会创建一个添加了新元素的原始列表的副本。不可变列表的思想是避免数据就地更新,是一种防御拷贝的技术,可以防止其他线程的并发突变
本篇重点的学习都是在不可变列表 上,因为它避免就地更新的优点,体现了编程中数据不可变的原则,是一种出于安全编程考虑更优的列表选择。
但是它是有局限性的,争议点主要是在添加元素上:
- 如果使用添加的元素,来创建列表的新副本是 一个耗时且栈内存的过程,则不可变的数据结构是会导致性能低下
这个观点确实是正确的,因为每次修改列表,就需要面对一个完整的数据结构,并将其复制。 这也是 Kotlin 不可变列表的情况。但是也有解决的办法,我们下面就是来解决这些问题。
为了处理不可变持久化列表,Kotlin 创建了很多高性能的函数, 我们可以通过学习这些函数,来了解高效的思想。
1.1 使用持久数据结构
这里的持久数据结构并不是指 SharedPreferences 这种持久化技术, 而是一种提高列表性能的技术。
对于不可变列表,在插入元素之前复制数据结构是一项耗时的操作,这会导致性能低下,但是如果使用了 数据共享(data sharing) 则会优化这种操作。
下图就展示了如果删除、添加元素,以创建一个新的具有最佳新能的不可变单链表:
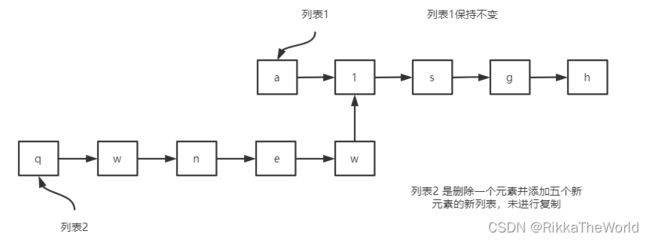
上图中的过程中,没有数据复制发生,这样的列表对于删除和插入元素可能比可变列表更高效,但是实际上还要看情况而定的。
1.2 实现不可变的、持久的单链表
上图的单链表结构是理论上的,列表无法实现这种形式,因为元素之间无法连接。但是我们可以通过定义递归的数据结构来设计一个单链表。对列表结构定义如下:
- 将列表的第一个元素,称为头元素
- 列表的其余部分,本身就是列表,称为尾部
- 空列表表示 Nil ,既没有头部也没有尾部
使用密封类,因为它是隐私抽象的,而且能限制不被他人继承,只用定义我们想要的结构就好:
sealed class List<A> {
abstract fun isEmpty(): Boolean
// 扩展类在列表类内定义,并成为私有类
private object Nil : List<Nothing>() {
override fun isEmpty(): Boolean = true
override fun toString(): String = "[NIL]"
}
private class Cons<A>(
internal val head: A,
internal val tail: List<A>
): List<A>() {
override fun isEmpty(): Boolean = false
override fun toString(): String = "[${toString("", this)}NIL]"
tailrec fun toString(acc: String, list: List<A>): String = when(list) {
is Nil -> acc
is Cons -> toString("$acc${list.head}, ", list.tail)
}
}
companion object {
// foldRight 的第一个参数是将 Nil 显示转化为 list
operator fun <A> invoke(vararg az: A): List<A> =
az.foldRight(Nil as List<A>) { a, acc ->
// 使用反向递归从后包到前
Cons(a, acc)
}
}
}
接下来就可以直接使用:
val list = MyList("a","b","c","d","e")
print(list)
// 打印
[a, b, c, d, e, NIL]
2. 列表操作中的数据共享
使用单链表的一个巨大好处,就是数据共享带来的性能提升, 例如访问列表的第一个元素、删除一个元素等。下面将举几个例子。
1. 添加头元素
我们来实现一个函数 cons(), 在列表的开头添加元素,答案很简单,我们其实在前面就已经实现了:
fun cons(a: A): MyList<A> = Cons(a, this)
2. 设置头元素
接下来,实现一个函数 setHead, 一个用新值替换 List 的第一个元素的函数,其实就是对第一个元素的尾部设置头元素:
fun setHead(a: A): MyList<A> = when(this) {
Nil -> throw IllegalStateException("setHead called on an empty list")
is Cons -> tail.cons(a)
}
3. 删除前n个元素
现在需要在不改变或创建任何内容的情况下删除列表的前n个元素:
// 这里使用共递归优化堆栈,并且对类型做判断
fun drop(n: Int): MyList<A> {
tailrec fun drop(n: Int, list: MyList<A>): MyList<A> =
if (n <= 0) list
else when (list) {
is Cons -> drop(n - 1, list.tail)
is Nil -> list
}
return drop(n, this)
}
4. 从头删除元素直到条件为false
我们可以把辅助函数放到伴生对象中,这样可以使得内部其他地方也可以访问辅助函数,增强重用性。 但是不放也行,视情况而定,取决于代码风格或需求:
fun dropWhile(p: (A) -> Boolean): MyList<A> = dropWhile(this, p)
companion object {
private tailrec fun <A> dropWhile(list: MyList<A>, p: (A) -> Boolean): MyList<A> = when (list) {
Nil -> list
is Cons -> if (p(list.head)) dropWhile(list.tail, p) else list
}
}
5. 连接列表
列表上的常见操作包括向另一个列表添加一个列表,形成包含两个列表所有元素的新表。
两个列表无法直接连接,但是可以通过将 前面列表的尾部元素 作为后面列表的头部元素,递归到前面列表的最前面,就可以得到新列表。如下图所示:

可以看到,列表1、2都被保留了,结果列表共享了列表2,由于我们要从尾巴访问列表1,所以可以使用递归的形式
代码如下:
fun concat(list: MyList<A>): MyList<A> = concat(this, list)
companion object {
private fun <A> concat(list1: MyList<A>, list2: MyList<A>): MyList<A> = when (list1) {
Nil -> list2
is Cons -> concat(list1.tail, list2).cons(list1.head)
}
}
这种写法的缺点是,函数本身的复杂度是依赖 list1 的长度的,如果list1过长,会爆栈,由于连接列表是一个比较常规的操作,所以它还有更进一步的抽象空间,我们会在下面学习到。
6. 从列表末尾删除元素
虽然单链表不是这种操作的理想数据结构,但仍然能够实现它。
这里将 函数命名为 init , 而不是 dropLast,为什么这样命名,是遵循哈斯卡尔的风格:wiki:

我们可以通过反转列表去删除第一个再反转列表,代码如下:
fun reverse(): MyList<A> {
tailrec fun <A> reverse(acc: MyList<A>, list: MyList<A>): MyList<A> = when(list) {
Nil -> acc
is Cons -> reverse(acc.cons(list.head), list.tail)
}
return reverse(MyList.invoke(), this)
}
fun init(): MyList<A> = reverse().drop(1).reverse()
这是 Cons 类的实现, 在 Nil 类,init 函数会抛出异常。
2.1 使用递归对具有高阶函数的列表进行折叠
之前有学习过对列表进行折叠, 折叠同样也适用于持久化列表,对对于可变列表,可以选择通过迭代或递归实现操作。而对于持久化列表却不适合这种迭代方法,接下来考虑对数字列表进行常见的折叠操作。
下面编写一个函数,使用递归计算持久化整数列表中所有元素的和。
fun sum(ints: MyList<Int>): Int = when (ints) {
Nil -> 0
is Cons -> ints.head + sum(ints.tail)
}
但这是不会通过编译的,因为 Nil 不是 MyList 的子类型
2.2 使用型变
上面遇到的问题是 ,尽管 Nothing 类型是所有类型的子类型, 始终可以将 Nothing 向其它任何类型转化,但是不能将 MyList 强制转化成 List,这是因为 Java 的机制。
不过 Kotlin 提供了协变,我们要使 泛型A 在 MyList 中协变, 这就意味着需要声明其为 MyList:
sealed class MyList<out A> {
...
}
但是这样会引来报错:

使用协变后, 意味着 MyList 类不能所包含具有 类型A 入参的函数, 参数是函数的输入,所以它在 “in” 的位置,函数的返回则是 out 的位置。深入了解可以看这篇文章:深入理解Kotlin中的泛型(协变、逆变)
使用了协变后,我们不能在 in 的位置使用泛型A, 那这样我们可能就会认为很不合理或者疑惑:那我们该怎么样向 MyList 汇总添加元素呢?
假如我们实现一个抽象方法,并让每个子类来继承:
sealed class MyList<out A> {
abstract fun cons(a: A): MyList<A>
internal object Nil : MyList<Nothing>() {..
override fun cons(a: Nothing): MyList<Nothing> = Cons(a, this)
}
internal class Cons<out A>(
) : MyList<A>() {
...
}
会出现两种问题:
cons函数不能在 in 位置使用泛型A,编译不通过, 是前面已经遇到的- Nil 类的
cons函数被编译器标记为 Unrechable code, 即不可访问的函数。 这是因为 Nil 类中的 this 引用了一个MyList,假设调用了Nil.cons(1)将导致 1 强制转化为 Nothing, 这是不可行的,因为 Nothing 是 Int 的子类型
要理解 Nil 中发生了什么, 必须记住 Kotlin 是一门严格的语言,这意味着无论是否使用函数参数,都要对他们进行检查。
上面的主要的问题出现在了函数的参数, 即 override fun cons(a: Nothing), 当函数接收到 A 参数时,它会立即强制转化为接受者的参数类型 Nothing ,这会导致错误。 紧接着,元素就会被添加到一个 MyList 中。我们不需要将参数向下强制转化为 Nothing,所以为了解决这个问题,技巧是:
- 可以使用
@unsafevariance注释,通过 in 位置使用 A 来避免编译报错:
abstract fun cons(a: @UnsafeVariance A): MyList<A>
- 通过将实现放在父类中,避免向下强制转化:
fun cons(a: @UnsafeVariance A): MyList<A> = Cons(a, this)
这是告诉编译器,无需担心 cons 函数中的型变问题,出了问题由编程者来处承担。现在可以对 setHead、concat 函数使用这个注解:
fun setHead(a: @UnsafeVariance A)..
fun concat(list: MyList<@UnsafeVariance A>)...
这样我们有了更大的自由,但是责任也更大了,我们要确保使用这个技巧时,任何不安全的转换都不会失败。
此外,还有一种情况,就是创建一个 Empty 抽象类来表示空列表, 然后创建一个 Nil 单例对象。可以在 父类 MyList 中定义抽象函数, Cons 或 Empty 中具体实现, 例如这样:
sealed class EmptyMyList<A> {
fun cons(a: A): EmptyMyList<A> = Cons(a, this)
abstract class Empty<A> : EmptyMyList<A>() {
}
object Nil: Empty<Nothing>() {}
class Cons<A>(
...
) : EmptyMyList<A>()
fun concat(list: EmptyMyList<A>): EmptyMyList<A> = concat(this, list)
companion object {
private fun <A> concat(list1: EmptyMyList<A>, list2: EmptyMyList<A>): EmptyMyList<A> = when (list1) {
Nil -> list2
is Cons -> concat(list1.tail, list2).cons(list1.head)
}
}
}
这样 concat 函数就会报错

这个时候因为考虑 Empty 是抽象类,为了避免类型检查,我们就需要使用多态的形式来实现 concat 函数了:
object Nil: Empty<Nothing>() {
override fun funconcat(list: EmptyMyList<Nothing>): EmptyMyList<Nothing> = list
}
class Cons<A>(
) : EmptyMyList<A>() {
override fun funconcat(list: EmptyMyList<A>): EmptyMyList<A> = Cons(this.head, list.concat(this.tail))
}
下面继续来编写几个函数。
7. 编写函数使用递归计算双精度列表中所有元素的乘积
空列表的乘积元素应该是1, 就和 sum 累加元素中的0是一样的。代码如下所示:
private fun product(ints: MyList<Double>): Double = when (ints) {
Nil -> 1.0
is Cons -> ints.head * product(ints.tail)
}
现在来看看 sum 和 product 的定义,我们能够抽出一个抽象的模型公式吗? 他们函数如下:
fun product(ints: MyList<Double>): Double ... 上面的
fun sum(ints: MyList<Int>): Int = when (ints) {
MyList.Nil -> 0
is MyList.Cons -> ints.head + sum(ints.tail)
}
我们先消除他们的差异,用一个通用符号来替换:
fun product(ints: MyList<Type>): Type = when (ints) {
MyList.Nil -> identity
is MyList.Cons -> ints.head operator operation(ints.tail)
}
fun sum(ints: MyList<Type>): Type = when (ints) {
MyList.Nil -> identity
is MyList.Cons -> ints.head operator operation(ints.tail)
}
这两个函数的 Type、operation、 identity、operator 的值有所不同,如果能找到一种方法来抽象这些公共部分,那么必须提供变量信息,以便在不重复的情况下实现这两个函数值。 这个常见的操作就是折叠(fold),之前也有学习过。下面实现一个 foldRight 并将其应用于求和与求积:
fun <A, B> foldRight(list: MyList<A>, identity: B, f: (A) -> (B) -> B): B =
when (list) {
MyList.Nil -> identity
is MyList.Cons -> f(list.head)(foldRight(list.tail, identity, f))
}
fun sum(list: MyList<Int>): Int = foldRight(list, 0) { x -> { y -> x + y } }
fun product(list: MyList<Double>): Double = foldRight(list, 1.0) { x -> { y -> x * y } }
因为结果与输入元素的类型相同, 所以这种情况下, 应该被称为 减少(reduce) , 而不是 折叠(fold)。 我们可以将 foldRight 函数放在伴生对象中,然后添加一个函数为参数的实例函数,该函数在 MyList 类中调用 foldRight:
class MyList{
...
fun <B> foldRight(identity: B, f: (A) -> (B) -> B): B = foldRight(this, identity, f)
8. 编写一个函数,来计算列表长度, 使用 foldRight 函数
// 没有用到的第一个参数是可以省略的
fun length(): Int = foldRight(0) { { it + 1 } }
由于 foldRight 是递归的而非尾递归的,所以可能会有爆栈的情况,我们需要优化成在恒定时间内获取列表的长度,所以需要使用性能更优的 foldLeft 函数。
tailrec fun <A, B> foldLeft(acc: B, list:MyList<A>, f: (B) -> (A) -> B): B = when(list) {
Nil -> acc
is Cons -> foldLeft(f(acc)(list.head), list.tail, f)
}
...
fun <B> foldLeft(identity: B, f: (B) -> (A) -> B): B = foldLeft(identity, this, f)
好的,这样我们来使用 foldLeft 来把 sum、 product、length、reverse、foldRight 优化成新的栈安全的版本:
fun sum(list: MyList<Int>): Int = list.foldLeft(0) { x -> { y -> x + y } }
fun product(list: MyList<Double>): Double = list.foldLeft(1.0) { x -> { y -> x * y } }
fun length(): Int = foldLeft(0) { i -> { i + 1 } }
fun reverse(): MyList<A> = foldLeft(invoke()) { acc -> { acc.cons(it) } }
fun <B> foldRightViaFoldLeft(identity: B, f: (A) -> (B) -> B) = this.reverse().foldLeft(identity) { x -> { y -> f(y)(x) } }
2.3 创建 foldRight 的栈安全递归的版本
之前说的 foldRight 的实现是基于栈的,不应该在实际项目中实现,性能不够优秀, 那我们是否可以优化成共递归的版本,并且不显示的使用 foldLeft 呢? 答案是可以的。
我们可以使用反转列表来处理:
// 在伴生对象中编写辅助函数,在 List 类中编写主函数
private tailrec fun <A, B> coFoldRight(acc: B, list: MyList<A>, identity: B, f: (A) -> (B) -> B): B =
when (list) {
Nil -> acc
is Cons -> coFoldRight(f(list.head)(acc), list.tail, identity, f)
}
....
fun <B> coFoldRight(identity: B, f: (A) -> (B) -> B): B = coFoldRight(identity, this.reverse(), identity, f)
但这种做法是有缺陷的,它强制处理了列表(反转),这掩盖了向右折叠的优点
9. 根据 foldLeft 或 foldRight 来实现 concat
通过 foldRight 我们可以轻松实现:
fun <A> concatViaFoldRight(list1: MyList<A>, list2: MyList<A>): MyList<A> =
foldRight(list1, list2, { x -> { y -> Cons(x, y) } })
而 foldLeft 则要反转列表,实现效率比较低:
fun <A> concatViaLeft(list1: MyList<A>, list2: MyList<A>): MyList<A> =
list1.reverse().foldLeft(list2) { x -> x::cons }
// 上面 { x -> x::cons } 等价于: { x -> { y -> x.cons(y) } }
10. 编写一个函数, 将一个列表组扁平化为包含每个子类表所有元素的列表
使用 foldRight 来实现也很轻松:
fun <A> flatten(list: MyList<A>): MyList<A> = list.foldRight(Nil) { x -> x::concat }
3. 小结
- 通过自定义一个单链表的数据结构,了解列表操作,如 sum、product、length、reverse等等
- 单链表是一个高效的数据结构,具有不可变列表的有点,同时允许修改,因为列表不可变,所以性能有所提高
- 可以通过递归引用函数来折叠列表
- 使用共递归处理列表,不会有栈溢出的风险
- 一旦定义了 foldLeft、foldRight 就不需要再次使用递归来处理列表了,因为它们已经抽象了递归。